专题02 函数-备战2018年高考数学（文）之纠错笔记系列

专题02 函数-备战2018年高考数学（文）之纠错笔记系列

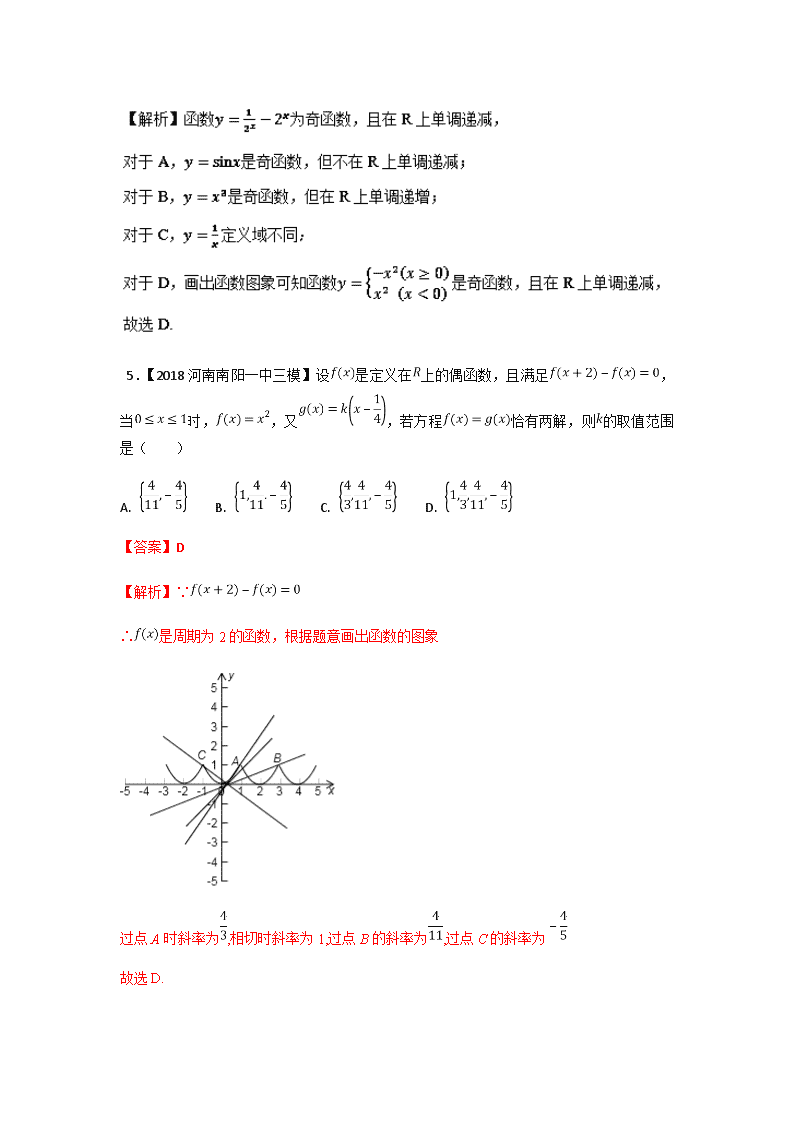
一、选择题 ‎1．【2018河北武邑中学调研二】已知， ， ， ，则的大小关系是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎ ‎ ‎2．【2018江西省新余一中二模】用表示不大于实数的最大整数，如，设分别是方程， 的根，则（ ）‎ A. 2 B. 3 C. 4 D. 5‎ ‎【答案】C ‎【解析】因为分别是方程， 的根，所以分别是及的零点，由于 是单调递增函数，又，所以，由 在定义域内递增且 可 ‎， ，故选C. ‎ ‎3．【2018衡水金卷高三联考】设，，，则的大小关系为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由题意得，.‎ 得，而.‎ 所以，即<1.【来.源：全,品…中&高*考*网】‎ 又.故.‎ 选A. ‎ ‎4．【2018衡水金卷高三联考】下列函数中，与函数的定义域、单调性与奇偶性均一致的函数是（ ）‎ A. B. ‎ C. D. 【来.源：全,品…中&高*考*网】‎ ‎【答案】D ‎ 5．【2018河南南阳一中三模】设是定义在上的偶函数，且满足，当时，，又，若方程恰有两解，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】∵‎ ‎∴是周期为2的函数，根据题意画出函数的图象 过点A时斜率为,相切时斜率为1,过点B的斜率为,过点C的斜率为 故选D. ‎ 点睛：本题考查利用函数解决方程问题.一个是转为函数零点问题，利用二分法求解，另一个是化原函数为两个函数，利用两个函数的交点来求解.本题采用第二种方法，首先由，变为两个函数，先画出在时的图象，然后利用函数的对称性和周期性得到的图象，再画的直线，由图求解即可.‎ ‎6．【2018河南南阳一中三模】已知函数是定义在上的偶函数，且在区间上单调递增.若实数满足，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎ 【来.源：全,品…中&高*考*网】‎ ‎7．【2018广东茂名五校联考】已知幂函数的图象过点，则函数在区间上的最小值是( )‎ A. B. 0 C. D. ‎ ‎【答案】B ‎【解析】由题设，故在上单调递增，则当 时取最小值，应选答案B。‎ 点睛：求函数最值的一般方法即为利用函数的单调性.研究函数单调性的一般方法：‎ ‎（1）直接利用基本初等函数的单调性；‎ ‎（2）利用定义判断函数单调性；‎ ‎（3）求导得函数单调性.‎ ‎8．【2018湖南永州市一模】已知定义在上的可导函数的导函数为，若对于任意实数有，且，则不等式的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎ 9．【2018湖南永州市一模】定义在上的偶函数满足，当时，，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】∵由题意可得函数是以2为周期的周期函数且为偶函数，当时，，∴，，，，‎ ‎，则成立，故选C. ‎ ‎10．【2018河南中原名校质检二】定义在上的函数，满足，且，若，则方程在区间上所有实根之和为（ ）‎ A. 3 B. 4 C. 5 D. 6‎ ‎【答案】C ‎ 11．【2018河南中原名校质检二】若方程的一个根在区间内，另一根在区间内，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D【来.源：全,品…中&高*考*网】‎ ‎【解析】方程的一个根在区间内，另一根在区间内，则令,, ‎ 画出区域：‎ ‎ ‎ A(-3,1) C(-1,0)‎ 点D（2,3）表示区域中的点（a,b）与点D（2,3）的斜率，由图可知 故答案为D ‎12．【2018河南中原名校质检二】函数的大致图象是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎ ‎ ‎13．【2018河南中原名校质检二】已知函数在区间上是减函数，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎ ‎ ‎14．【2018河南中原名校质检二】定义在上的函数，满足，则（ ）‎ A. B. C. 1 D. 2‎ ‎【答案】A ‎【解析】‎ 故选A ‎15．【2018湖南两市九月调研】若，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由对数函数的性质可得， 由指数函数的性质可得 ，故选B.‎ ‎16．【2018广西联考】已知定义在上的奇函数在上递减，若对恒成立，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由已知可得 在 上是减函数，故原命题等价于，即 ‎ 在 上恒成立，设，令，当 时 ，当 时 ，因此 ，故选C.‎ ‎【点睛】本题关键步骤有：1.利用奇函数的性质可得 在 上是减函数；2.将原命题等价转化为 在上恒成立；3.利用导数工具求得，从而求得正解.‎ ‎17．【2018广西联考】函数的单调递增区间为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎ 18．【2018吉林百校联盟九月联考】已知函数函数，则下列说法错误的是（ ）‎ A. 若，则函数无零点 B. 若，则函数有零点 C. 若，则函数有一个零点 D. 若，则函数有两个零点 ‎【答案】A ‎【解析】作出函数的图象如图所示：‎ 观察可知：当时，函数有一个零点，故A错误.‎ 故选：A ‎19．【2018辽宁省沈阳市育才学校一模】若函数与 存在相同的零点，则的值为（ ）‎ A. 4或 B. 4或 C. 5或 D. 6或 ‎【答案】C ‎【解析】将函数 的零点 代入 得到 ‎ ，解得 或，故选C ‎20．【2018辽宁省沈阳市育才学校一模】下列函数的图像关于轴对称的是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】验证只有D选项， 满足是偶函数定义，故图象关于轴对称，选D.‎ ‎21．【2018广西柳州市一模】函数的图象大致是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎ 22．【2018超级全能生26省联考】已知函数有三个零点，则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】显然不满足三个零点，所以， ，当时， （）两图像必有一交点，所以必有一零点在。当x>0时， 所以f(x)在单调递减，在上单调递增。上要有两个零点，只需，解得，选D.‎ ‎【点睛】‎ 零点问题，常把方程F(x)=0变形为左右两边各放一个函数f(x)=g(x),然后分别出来 y=f(x)和y=g(x)的图像，再观察两图像交点个数，从而得到y=F(x)的零点个数。如果图像不好直接画出，则要借助导数及函数图像来解决。‎ ‎23．【2018吉林长春市一模】已知定义在上的奇函数满足，当时，，则函数在区间上所有零点之和为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎ 24．【2018广东海珠区一模】已知是自然对数的底数，函数的零点为，函数的零点为，则下列不等式中成立的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎ 25．【2018广东广州海珠区一模】若函数为奇函数， ，则不等式的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】∵函数为奇函数，‎ ‎∴f(0)=0，‎ 即a=−1，‎ ‎∴，‎ 当x>0时,解g(x)=−lnx>1得：x∈(0,e−1)，‎ 当x<0时,解g(x)= >1得：x∈(−∞,0)，【来.源：全,品…中&高*考*网】‎ 故不等式g(x)>1的解集为(−∞,0)∪((0,e−1)，‎ 故选：C ‎26．【2018贵州遵义航天高级中学一模】定义域为上的奇函数满足，且，则（ ）‎ A. 2 B. 1 C. -1 D. -2‎ ‎【答案】C ‎【解析】 ,因此 ，选C.‎ ‎27．【2018贵州遵义航天高级中学一模】已知, ,若,则下列结论中,不可能成立的是(   )‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】, ,所以，因此 ‎ 即或或，因此选B.‎ ‎28．【2018河北武邑中学一模】已知函数f（x）是定义在R上的偶函数，若任意的x≥0，都有f（x+2）=-f（x），当x∈[0,1]时，f（x）=2x-1，则f（-2017）+f（2018）=‎ A. 1 B. -1 C. 0 D. 2‎ ‎【答案】A ‎ ‎