高考数学专题复习课件：13-4 算法与程序框图

高考数学专题复习课件：13-4 算法与程序框图

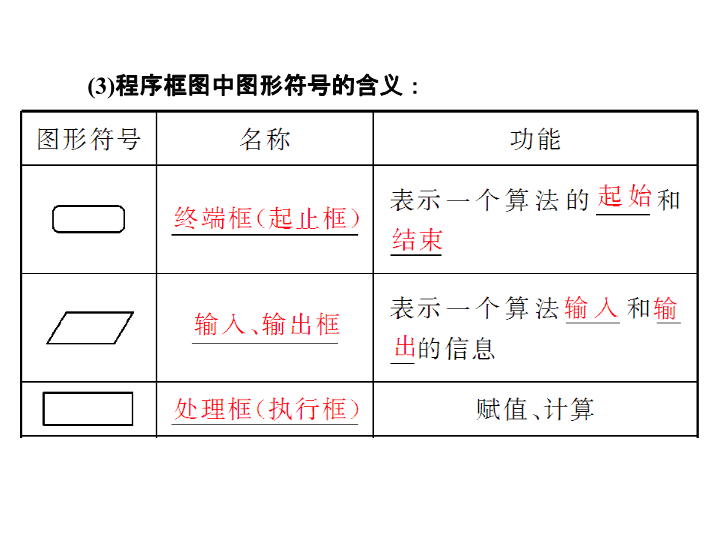
§13.4 　算法与程序框图 [ 考纲要求 ] 　 1. 了解算法的含义，了解算法的思想； 2. 理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构 .3. 理解几种基本算法语句 —— 输入语句、输出语句、赋值语句、条件语句、循环语句的含义． 1 ． 算法的含义与程序框图 (1) 算法：算法是指按照一定规则解决 _______ 问题的明确和 ________ 步骤． (2) 程序框图：程序框图又称流程图，是一种用 ________ 、 _______ 及 __________ 来表示算法的图形． 某一类 有限的 程序框 流程线 文字说明 (3) 程序框图中图形符号的含义： 2. ( 人教 A) 三种基本逻辑结构及相应语句 2. ( 人教 B) 三种基本逻辑结构 (1) 顺序结构描述的是最简单的算法结构，语句与语句之间，框与框之间按从 ____ 到 ____ 的顺序进行． (2) 条件分支结构，它是依据 _______________ 选择执行 ___________ 的控制结构． (3) 根据 ________ 决定是否重复执行 ________________ 的控制结构称为循环结构． 上 下 指定条件 不同指令 指定条件 一条或多条指令 3 ． ( 人教 B) 赋值、输入和输出语句 (1) 赋值语句 ① 概念：用来表明赋给某一个变量一个 ___________ 的语句． ② 一般格式： ______________ ． ③ 作用：先计算出 __________________ 的值，然后把该值赋给 _________________ ，使该变量的值等于 ________ 的值． 具体确定值 变量名＝表达式 赋值号右边表达式 赋值号左边的变量 表达式 (2) 输入语句 ① 概念：用来控制 ______________ 的语句． ② 作用：把 ______ 和 ___________ 分开． (3) 输出语句 ① 概念：用来控制把 ______________ 在屏幕上显示 ( 或打印 ) 的语句． ② 作用： ________________ ． 输入相应数值 程序 初始数据 求解的结果 把求解结果输出来 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 算法只能解决一个问题，不能重复使用． ( 　　 ) (2) 程序框图中的图形符号可以由个人来确定． ( 　　 ) (3) 输入框只能紧接开始框，输出框只能紧接结束框． ( 　　 ) (4) 条件结构的出口有两个，但在执行时，只有一个出口是有效的． ( 　　 ) (5)5 ＝ x 是赋值语句． ( 　　 ) (6) 输入语句可以同时给多个变量赋值． ( 　　 ) 【 答案 】 (1) × 　 (2) × 　 (3) × 　 (4) √ 　 (5) × 　 (6) √ 1 ．已知一个算法： (1) m ＝ a . (2) 如果 b < m ，则 m ＝ b ，输出 m ；否则执行第 (3) 步． (3) 如果 c < m ，则 m ＝ c ，输出 m . 如果 a ＝ 3 ， b ＝ 6 ， c ＝ 2 ，那么执行这个算法的结果是 ( 　　 ) A ． 3 　　　　　　　　　　 B ． 6 C ． 2 D ． m 【 解析 】 当 a ＝ 3 ， b ＝ 6 ， c ＝ 2 时，依据算法设计，本算法是求 a 、 b 、 c 三个数的最小值，故输出 m 的值为 2 ，故选 C. 【 答案 】 C 2 ． (2015· 陕西 ) 根据如图所示的框图，当输入 x 为 6 时，输出的 y 等于 ( 　　 ) A ． 1 B ． 2 C ． 5 D ． 10 【 解析 】 输入 x ＝ 6 ， 程序运行情况如下： x ＝ 6 － 3 ＝ 3 ＞ 0 ， x ＝ 3 － 3 ＝ 0 ≥ 0 ， x ＝ 0 － 3 ＝－ 3 ＜ 0 ， 退出循环，执行 y ＝ x 2 ＋ 1 ＝ ( － 3) 2 ＋ 1 ＝ 10 ， 输出 y ＝ 10. 故选 D. 【 答案 】 D 3 ． (2016· 北京 ) 执行如图所示的程序框图，若输入的 a 值为 1 ，则输出的 k 值为 ( 　　 ) A ． 1 B ． 2 C ． 3 D ． 4 【 答案 】 B 4 ． (2015· 北京 ) 执行如图所示的程序框图，输出的结果为 ( 　　 ) A ． ( － 2 ， 2) B ． ( － 4 ， 0) C ． ( － 4 ，－ 4) D ． (0 ，－ 8) 【 解析 】 第一次循环： s ＝ 1 － 1 ＝ 0 ， t ＝ 1 ＋ 1 ＝ 2 ， x ＝ 0 ， y ＝ 2 ， k ＝ 1 ， k ≥ 3 不成立；第二次循环： s ＝ 0 － 2 ＝－ 2 ， t ＝ 0 ＋ 2 ＝ 2 ， x ＝－ 2 ， y ＝ 2 ， k ＝ 2 ， k ≥ 3 不成立；第三次循环： s ＝－ 2 － 2 ＝－ 4 ， t ＝－ 2 ＋ 2 ＝ 0 ， x ＝－ 4 ， y ＝ 0 ， k ＝ 3 ， k ≥ 3 成立．跳出循环，输出 ( － 4 ， 0) ．故选 B. 【 答案 】 B 5 ． ( 教材改编 ) 程序： 上面程序表示的函数是 ________ ． 题型一　顺序结构与条件结构 命题点 1 　顺序结构 【 例 1 】 已知 f ( x ) ＝ x 2 － 2 x － 3. 求 f (3) 、 f ( － 5) 、 f (5) ，并计算 f (3) ＋ f ( － 5) ＋ f (5) 的值．设计出解决该问题的一个算法，并画出程序框图． 【 解析 】 算法如下： 第一步，令 x ＝ 3. 第二步，把 x ＝ 3 代入 y 1 ＝ x 2 － 2 x － 3. 第三步，令 x ＝－ 5. 第四步，把 x ＝－ 5 代入 y 2 ＝ x 2 － 2 x － 3. 第五步，令 x ＝ 5. 第六步，把 x ＝ 5 代入 y 3 ＝ x 2 － 2 x － 3. 第七步，把 y 1 ， y 2 ， y 3 的值代入 y ＝ y 1 ＋ y 2 ＋ y 3 . 第八步，输出 y 1 ， y 2 ， y 3 ， y 的值． 该算法对应的程序框图如图所示： 【 答案 】 C 【 方法规律 】 应用顺序结构与条件结构的注意点 (1) 顺序结构 顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的． (2) 条件结构 利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足． A ． [ － 3 ，－ 2] B ． [ － 2 ，－ 1] C ． [ － 1 ， 0] D ． [0 ， 1] 【 答案 】 B 题型二　循环结构 命题点 1 　由程序框图求输出结果 【 例 3 】 (2015· 安徽 ) 执行如图所示的程序框图，输出的 n 为 ________ ． 【 答案 】 4 命题点 2 　完善程序框图 【 例 4 】 (2017· 湖南东部六校联考 ) 如图是计算某年级 500 名学生期末考试 ( 满分为 100 分 ) 及格率 q 的程序框图，则图中空白框内应填入 ( 　　 ) 【 答案 】 D 【 答案 】 a n ＝ 2 n － 1 【 方法规律 】 与循环结构有关问题的常见类型及解题策略 (1) 已知程序框图，求输出的结果，可按程序框图的流程依次执行，最后得出结果． (2) 完善程序框图问题，结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式． (3) 对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断． A ． n ＝ 6? B ． n ＜ 6? C ． n ≤ 6? D ． n ≤ 8? (2) (2017· 黄冈模拟 ) 随机抽取某中学甲、乙两个班各 10 名同学，测量他们的身高获得身高数据的茎叶图如图，在样本的 20 人中，记身高在 [150 ， 160) ， [160 ， 170) ， [170 ， 180) ， [180 ， 190) 的人数依次为 A 1 ， A 2 ， A 3 ， A 4 . 如图是统计样本中身高在一定范围内的人数的算法框图．若图中输出的 S ＝ 18 ，则判断框应填 ________ ． (2) 由于 i 从 2 开始，也就是统计大于或等于 160 的所有人数，于是就要计算 A 2 ＋ A 3 ＋ A 4 ，因此，判断框应填 i ＜ 5 ？或 i ≤ 4 ？ . 【 答案 】 (1)C 　 (2) i ＜ 5 ？或 i ≤ 4? 题型三　基本算法语句 【 例 6 】 根据下列算法语句，当输入 x 为 60 时，输出 y 的值为 ( 　　 ) A ． 25 B ． 30 C ． 31 D ． 61 【 答案 】 C 【 方法规律 】 解决算法语句有三个步骤：首先通读全部语句，把它翻译成数学问题；其次领悟该语句的功能；最后根据语句的功能运行程序，解决问题． 跟踪训练 3 设计一个计算 1 × 3 × 5 × 7 × 9 × 11 × 13 的算法．图中给出了程序的一部分，则在横线上不能填入的数是 ( 　　 ) A ． 13 B ． 13.5 C ． 14 D ． 14.5 【 解析 】 当填 i <13 时， i 值顺次执行的结果是 5 ， 7 ， 9 ， 11 ，当执行到 i ＝ 11 时，下次就是 i ＝ 13 ，这时要结束循环，因此计算的结果是 1 × 3 × 5 × 7 × 9 × 11 ，故不能填 13 ，但填的数字只要超过 13 且不超过 15 均可保证最后一次循环时，得到的计算结果是 1 × 3 × 5 × 7 × 9 × 11 × 13. 【 答案 】 A 易错警示系列 21 变量的含义理解不准致误 【 典例 】 执行如图所示的程序框图，输出的 S 值为 ( 　　 ) A ． 2 B ． 4 C ． 8 D ． 16 【 易错分析 】 (1) 读不懂程序框图，把执行循环体的次数 n 误认为是变量 k 的值，没有注意到 k 的初始值为 0. (2) 对循环结构： ① 判断条件把握不准； ② 循环次数搞不清楚； ③ 初始条件容易代错． 【 解析 】 当 k ＝ 0 时，满足 k <3 ，因此 S ＝ 1 × 2 0 ＝ 1 ； 当 k ＝ 1 时，满足 k <3 ，则 S ＝ 1 × 2 1 ＝ 2 ； 当 k ＝ 2 时，满足 k <3 ，则 S ＝ 2 × 2 2 ＝ 8 ； 当 k ＝ 3 时，不满足 k <3 ，输出 S ＝ 8. 【 答案 】 C 【 温馨提醒 】 (1) 要分清是当型循环结构还是直到型循环结构；要理解循环结构中各变量的具体含义以及变化规律． (2) 在处理含有循环结构的算法问题时，关键是确定循环的次数，循环中有哪些变量，且每一次循环之后的变量 S 、 k 值都要被新的 S 、 k 值所替换 . ► 方法与技巧 1 ．在设计一个算法的过程中要牢记它的五个特征： 概括性、逻辑性、有穷性、不唯一性、普遍性． 2 ．在画算法框图时首先要进行结构的选择．若所要解决的问题不需要分情况讨论，只用顺序结构就能解决；若所要解决的问题要分若干种情况讨论时，就必须引入条件结构；若所要解决的问题要进行许多重复的步骤，且这些步骤之间又有相同的规律时，就必须引入变量，应用循环结构． ► 失误与防范 1 ．注意起止框与处理框、判断框与循环框的不同． 2 ．注意条件结构与循环结构的联系：对于循环结构有重复性，条件结构具有选择性没有重复性，并且循环结构中必定包含一个条件结构，用于确定何时终止循环体． 3 ．循环语句有 “ 直到型 ” 与 “ 当型 ” 两种，要区别两者的异同，主要解决需要反复执行的任务，用循环语句来编写程序． 4 ．关于赋值语句，有以下几点需要注意： (1) 赋值号左边只能是变量名字，而不是表达式，例如 3 ＝ m 是错误的． (2) 赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如 Y ＝ x ，表示用 x 的值替代变量 Y 的原先的取值，不能改写为 x ＝ Y . 因为后者表示用 Y 的值替代变量 x 的值． (3) 在一个赋值语句中只能给一个变量赋值，不能出现多个 “ ＝ ” .