湖北省孝感市2018-2019学年高二下学期期中考试数学（理）试卷

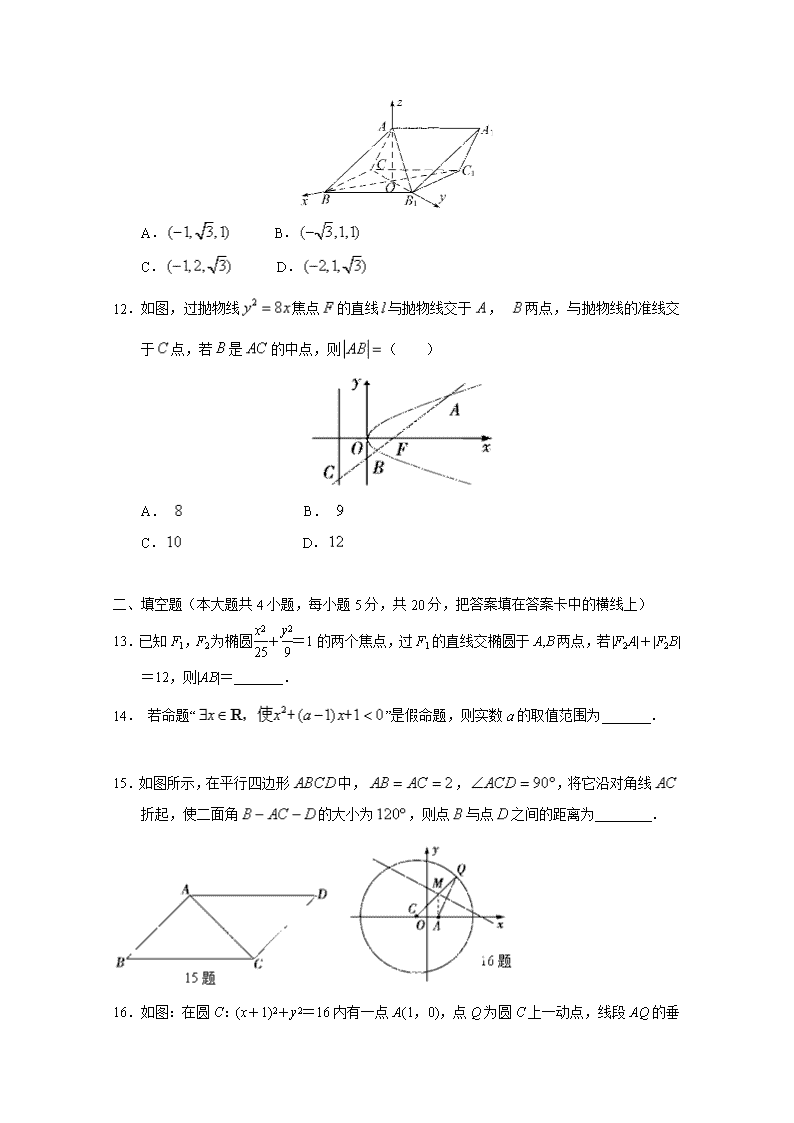
湖北省孝感市2018-2019学年高二下学期期中考试数学（理）试卷

‎2018-2019学年度下学期 孝感市部分普通高中联考协作体期中联合考试 高二理科数学试卷 命题人：马云飞 审题人：熊燕霞 本试题卷共4页，满分150分，考试时间120分钟。‎ 注意事项：‎ 1． 答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证条形码粘贴在答题卡上的指定位置。‎ 2． 选择题的作答：每小题选出答案后，用2B铅笔把答题卡对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3．非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4．考试结束后，请将本试卷和答题卡一并上交。 ‎ 一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．命题“”的否定是（ ）‎ A． B．‎ C． D．‎ ‎2．抛物线的焦点坐标是(　　 ) ‎ A．(0，2)　　 B．　　 C．　 　 D．(0，4)‎ ‎3．若直线的方向向量，平面的一个法向量，若，则实数（ ）‎ A．2 B． C． D．10‎ ‎4．过抛物线的焦点作直线l交抛物线于A、B两点，若线段AB中点的横坐标为4，则等于（ ） ‎ A．10　 　 B．8　 　 C．6　 　　 D．4 ‎ ‎5．有下列三个命题：‎ ‎（1）“若，则”的否命题；（2）“若，则”的逆否命题；（3）“若，则”的逆命题．‎ 其中真命题的个数是(　　)‎ A． B． C． D．‎ ‎6．已知双曲线，点，为其两个焦点，点为双曲线上一点，若 则的面积是( )‎ A． B． C． D．‎ ‎7．已知二面角，其中平面的一个法向量，平面的一个法向量，则二面角的大小可能为(　　 )‎ A．　　 B．　　 C．或　　 D．‎ ‎8． 若直线与双曲线的左支交于不同的两点,则实数的取值范围是（ 　 ）‎ A．　　 B．　 　C．　　 D．‎ ‎9．已知，，若是的一个必要不充分条件，则的取值范围为（ ）‎ A．　　 B．　　 C．　　 D． ‎ ‎10．已知双曲线的渐近线均和圆相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为（ ）‎ A． B． C． D．‎ ‎11．如图三棱柱ABCA1B1C1中，侧面BB1C1C是边长为2菱形，∠CBB1＝60°，BC1 交B1C与点O，AO⊥侧面BB1C1C，且为等腰直角三角形，如图建立空间直角坐标系，则点A1的坐标为（ ）‎ A．　 B．　 ‎ C．　 D．‎ ‎12．如图，过抛物线焦点的直线与抛物线交于， 两点，与抛物线的准线交于点，若是的中点，则（ ）‎ A． B． ‎ C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答案卡中的横线上）‎ ‎13．已知F1，F2为椭圆＋＝1的两个焦点，过F1的直线交椭圆于A,B两点，若|F2A|＋|F2B|＝12，则|AB|＝_______．‎ ‎14． 若命题“”是假命题，则实数a的取值范围为_______．‎ ‎15．如图所示，在平行四边形中，，，将它沿对角线折起，使二面角的大小为，则点与点之间的距离为 ．‎ ‎16．如图：在圆C：(x＋1)2＋y2＝16内有一点A(1，0)，点Q为圆C上一动点，线段AQ 的垂直平分线与直线CQ的连线交于点M，根据椭圆定义可得点M的轨迹方程为；利用类比推理思想：在圆C：(x＋3)2＋y2＝16外有一点A(3，0)，点Q为圆C上一动点，线段AQ的垂直平分线与直线CQ交于点M，则点M的轨迹方程为 ．‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）‎ ‎17. (本题10分)给出下列命题：‎ ‎：方程表示的曲线是双曲线；‎ ‎：方程表示的曲线是一个圆；‎ ‎（1）若为真命题，求的取值范围；‎ ‎（1）若为真命题，求的取值范围．‎ ‎18．(本题12分)‎ ‎（1）如图（1）所示，椭圆的中心在原点，焦点F1、F2在x轴上，A、B是椭圆的顶点，P是椭圆上一点，且PF1⊥x轴，PF2∥AB，求此椭圆的离心率；‎ ‎（2）如图（2）所示，双曲线的一个焦点为F，虚轴的一个端点为B，如果直线FB与该双曲线的一条渐近线垂直，求此双曲线的离心率．‎ ‎19．(本题12分) 如图，直三棱柱中，是边长为2等边三角形，D是BC的中点．‎ ‎（1）求证：A1B∥平面ADC1；‎ ‎（2）若A1D与平面ABC所成角为，求A1D与 平面AC1D所成角的正弦值．‎ ‎20．(本题12分)已知点F为抛物线C：x2＝2py (p＞0) 的焦点，点A(m，3)在抛物线C上，且|AF|＝5，若点P是抛物线C上的一个动点，设点P到直线的距离为，设点P到直线的距离为．‎ ‎（1）求抛物线C的方程；‎ ‎（2）求的最小值；(2)求的最小值． ‎ ‎21．(本题12分)如图，在几何体ABCDEF中，四边形ABCD是菱形，BE⊥平面ABCD，DF∥BE，且DF＝2BE＝2，BD＝.‎ ‎（1）证明：平面ACE⊥平面BEFD；‎ ‎（2）若二面角AEFC是直二面角，求异面直线 AE与CF所成角的余弦值．‎ ‎22．(本题12分)已知椭圆的两个焦点分别为，，离心率为，且椭圆四个顶点构成的菱形面积为．‎ ‎（1）求椭圆C的方程；‎ ‎（2）若直线l ：y＝x＋m与椭圆C交于M，N两点，以MN 为底边作等腰三角形，顶点为P(3，－2)，求m的值及△PMN的面积．‎ ‎2018-2019学年度下学期孝感市普通高中联考协作体 期中联合考试 高二数学(理科)试卷【参考答案】‎ ‎1-12 ‎ ‎13． 14． 15． 16． (x≦-2) ‎ ‎17．【解析】：：---------2分 ‎： 由即 ---------4分 ‎（1）由为真命题 ---------7分 ‎（2）由为真命题------10分 ‎18．【解析】： （1）依题意、、、‎ ‎，，由∥得：---------3分 所求 --6分 ‎（2）依题意，‎ ‎；渐近线斜率：，由---------9分 由因为，所求 ---------12分 ‎19．【解析】：(1)证明：连接A1C交AC1于O，‎ 四边形AA1C1C为平行四边形，O为A1C中点，又D为BC中点，‎ 所以∥ ---------------5分 ‎ ‎(2) 因为△ABC是等边三角形，D是BC的中点，所以AD⊥BC．如图，‎ 以D为原点，建立如图所示空间坐标系． ‎ 由A1D与平面ABC所成角为 A A1＝A D＝ -------------7分 则D(0，0，0)，A(，0，0)，A1(，0，)，C1(0，-1，)，‎ 则＝(，0，0)，＝(0，-1，)， ‎ 设平面AC1D的一个法向量为＝(x，y，z)，‎ 则，即，‎ 取z＝1，则x＝0，y＝，‎ ‎∴＝(0，，1) -----------------------------------------------9分 又＝(，0，)，设A1D与平面ADC1所成角为θ，则 故所求A1D与平面ADC1所成角的正弦值为------------------------12分 ‎20．【解析】：(1)由抛物线的定义得，‎ ‎|AF|＝3＋＝5 -----------------------------------------------------------2分 解得p＝4，所以抛物线C的方程为-----------------------------4分 ‎（2）设直线的平行线：‎ ‎----------6分 所求 ------------------------------------------------8分 ‎（3）由直线是抛物线C的准线，∴=|PF| ----------------10分 所以最小值就等于F (0，2)到直线的距离：‎ 所求 --------------12分 ‎21．【解析】：‎ ‎ (1)证明：∵四边形ABCD是菱形，∴AC⊥BD-----①‎ ‎∵BE⊥平面ABCD，∴BE⊥AC----- ②， ∵BD∩BE＝B-----③‎ ‎∴由①②③：AC⊥平面BEFD，AC平面ACE，∴平面ACE⊥平面BEFD -----4分 ‎(2)设AC与BD的交点为O，由(1)得AC⊥BD，如图：分别以OA，OB为x轴和y轴，过点O作垂直于平面ABCD的直线为z轴，建立如图所示的空间直角坐标系Oxyz --- 5分 ‎∴BD＝2.设OA＝a(a＞0)，则A(a,0,0)，C(－a,0,0)，E(0，，1)，F(0，－，2)，‎ ‎∴＝(0，－2，1)，＝(－a，，1)，＝(a，，1)．----------------6分 设m＝(x1，y1，z1)是平面AEF的法向量，则，‎ 即，令z1＝，‎ ‎∴平面AEF的一个法向量为m＝ -----------------8分 同理设n＝(x2，y2，z2)，是平面CEF的法向量，则 得平面CEF的一个法向量为n＝-----------------9分 ‎∵二面角AEFC是直二面角，‎ ‎∴m·n＝-------------------------10分 ‎∵， 设异面直线AE与CF所成角为 故所求异面直线AE与CF所成角为的余弦值为 -------------12分 ‎22.【解析】： ‎ ‎（1）依题意： -----------2分 得所求椭圆C的方程为：-----------------4分 ‎（2）设M (x1，y1)，N(x2，y2)，MN的中点为Q(x0，y0)‎ 消去得：‎ ‎ ‎ ‎ 4应为16‎ 韦达定理：x0＝＝ ‎ y0＝x0＋m＝所以-----------------------6分 由 ‎ ‎ 满足-------9分 即--------10分 顶点(3，－2)到底边MN的距离------------11分 所求 --------------------------12分