- 2021-06-23 发布 |
- 37.5 KB |
- 3页


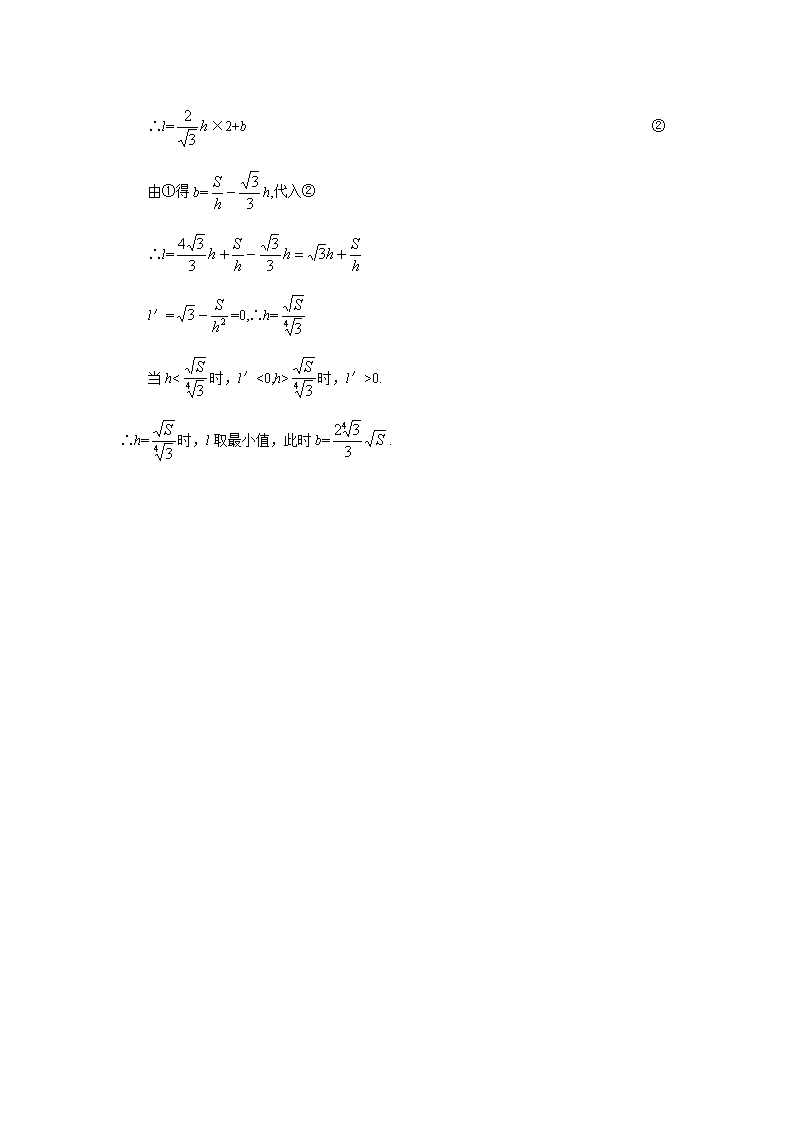
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学3_3_3 函数的最大值与最小值练习题
3. 3.3 函数的最大值与最小值练习题 一、选择题(本大题共6小题,每小题3分,共18分) 1.下列说法正确的是 A.函数的极大值就是函数的最大值B.函数的极小值就是函数的最小值 C.函数的最值一定是极值 D.在闭区间上的连续函数一定存在最值 2.函数y=f(x)在区间[a,b]上的最大值是M,最小值是m,若M=m,则f′(x) A.等于0 B.大于0 C.小于0 D.以上都有可能 3.函数y=,在[-1,1]上的最小值为 A.0 B.-2 C.-1 D. 4.下列求导运算正确的是( ) A. B. C. D. 5.设y=|x|3,那么y在区间[-3,-1]上的最小值是 A.27 B.-3 C.-1 D.1 6.设f(x)=ax3-6ax2+b在区间[-1,2]上的最大值为3,最小值为-29,且a>b,则 A.a=2,b=29 B.a=2,b=3 C.a=3,b=2 D.a=-2,b=-3 二、填空题(本大题共5小题,每小题3分,共15分) 7.函数y=2x3-3x2-12x+5在[0,3]上的最小值是___________. 8.已知函数f(x)=2-x2,g(x)=x.若f(x)*g(x)=min{f(x),g(x)},那么f(x)*g(x)的最大值是 . 9.将正数a分成两部分,使其立方和为最小,这两部分应分成____和____. 10.使内接椭圆=1的矩形面积最大,矩形的长为_____,宽为______ 11.在半径为R的圆内,作内接等腰三角形,当底边上高为______时,它的面积最大. 三、解答题(本大题共3小题,每小题9分,共27分) 12.有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,问剪去的小正方形的边长应为多少? 13.已知:f(x)=log3,x∈(0,+∞).是否存在实数a、b,使f(x)同时满足下列两个条件:(1)f(x)在(0,1)上是减函数,在[1,+∞)上是增函数;(2)f(x)的最小值是1,若存在,求出a,b,若不存在,说明理由. 14.一条水渠,断面为等腰梯形,如图所示,在确定断面尺寸时,希望在断面ABCD的面积为定值S时,使得湿周l=AB+BC+CD最小,这样可使水流阻力小,渗透少,求此时的高h和下底边长b. 函数的最大值与最小值 一、1.D 2.A 3.A 4.B 5.D 6.B 二、7. -15 8. 1 9. 10.a b 11.R 三、12.解:(1)正方形边长为x,则V=(8-2x)·(5-2x)x=2(2x3-13x2+20x)(0查看更多