2019届二轮复习选择填空标准练(1)作业(全国通用)
2019届二轮复习 选择填空标准练 (1) 作业(全国通用)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|x2>1},集合B={x|x(x-2)<0},则A∩B= ( )
A.{x|x≤1或x≥2} B.{x|x>2}
C.{x|0
1}={x|x>1或x<-1},B={x|x(x-2)<0}={x|01,0logb2 018
B.logba(c-b)ba
D.(a-c)ac>(a-c)ab
【解析】选D.根据对数函数的单调性可得loga2 018>0>logb2 018,logba1,00,
所以(c-b)ca>(c-b)ba,(a-c)ac<(a-c)ab,则C正确,D错误.
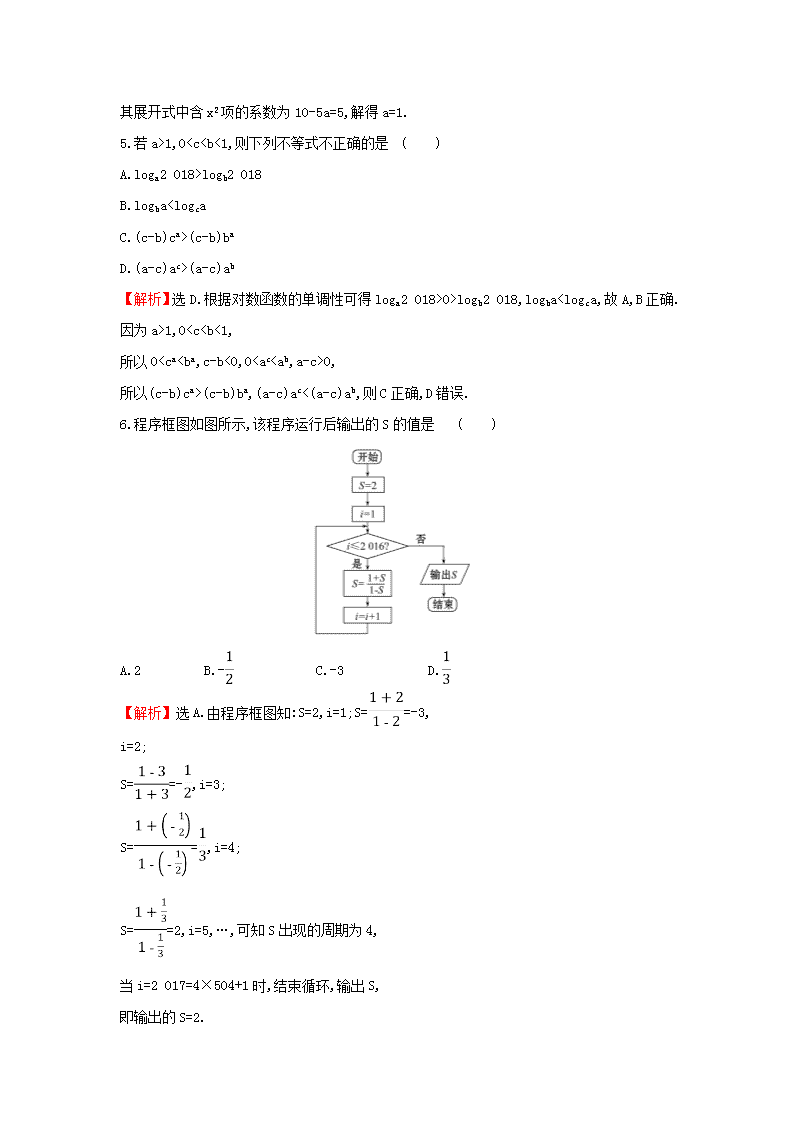
6.程序框图如图所示,该程序运行后输出的S的值是 ( )
A.2 B.- C.-3 D.
【解析】选A.由程序框图知:S=2,i=1;S==-3,
i=2;
S==-,i=3;
S==,i=4;
S==2,i=5,…,可知S出现的周期为4,
当i=2 017=4×504+1时,结束循环,输出S,
即输出的S=2.
7.设x,y满足约束条件则z=x-y的最小值是 ( )
A.0 B.-1 C.-2 D.-3
【解析】选C.如图作出不等式组对应的平面区域,由图可知,平移直线y=x-z.当直线经过点A(0,2)时,z有最小值-2.
8.设数列{an}是等差数列,且a2=-6,a6=6,Sn是数列{an}的前n项和,则 ( )
A.S4S1 D.S4=S1
【解析】选B.设等差数列{an}的公差为d.
因为a2=-6,a6=6,所以4d=a6-a2=12,即d=3.
所以an=-6+3(n-2)=3n-12.
所以S1=a1=-9,S3=a1+a2+a3=-9-6-3
=-18,
S4=a1+a2+a3+a4=-9-6-3+0=-18.
所以S40,b>0)的一条渐近线与直线x=0的夹角为30°,若以双曲线C的实轴和虚轴为对角线的四边形的面积为8,则双曲线C的标准方程为 ( )
A.-=1 B.-=1
C.-=1 D.-=1
【解析】选A.因为双曲线C:-=1(a>0,b>0)的一条渐近线与直线x=0的夹角为30°,所以双曲线C的渐近线方程为y=±x,所以=.因为以双曲线C的实轴和虚轴为对角线的四边形的面积为8,所以4×ab=8,即ab=4.由解得所以双曲线C的标准方程为-=1.
12.在△ABC中,角A,B,C的对边分别为a,b,c,若=,b=4,则△ABC面积的最大值为 ( )
A.4 B.2 C.3 D.
【解析】选A.因为=,
所以(2a-c)cos B=bcos C,
由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
所以2sin Acos B=sin Ccos B+sin Bcos C=sin(B+C)=sin A.
又sin A≠0,所以cos B=.
因为0
查看更多