- 2021-06-23 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年安徽省天长中学高二上学期第二次段考数学(文)试题 Word版
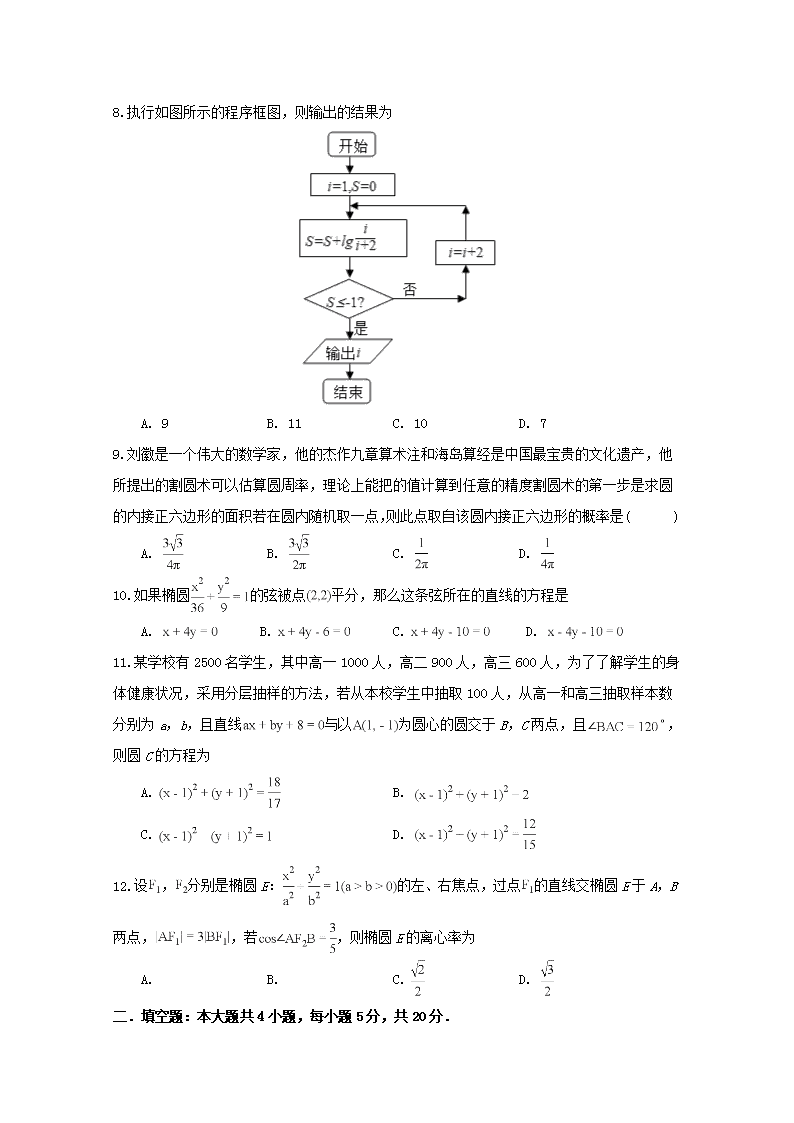
天长中学2018-2019学年度第一学期第二次段考 高二数学(文)试卷 一.选择题:每小题5分,共60分.在每小题给出的四个答案中,只有一项是符合题目要求的. 1.设全集为R,集合,,则 A. B. C. D. 2.已知命题p,q,那么“为真命题”是“为真命题”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 3, 某学校要从高一年级的752名学生中选取5名学生代表去敬老院慰问老人,若采用系统抽样方法,首先要随机剔除2名学生,再从余下的750名学生中抽取5名学生,则其中学生甲被选中的概率为 A. B. C. D. 4.设F为抛物线C:的焦点,过F且倾斜角为的直线交于C于A,B两点,则 A. B. 6 C. 12 D. 5.设m、n是两条不同的直线,、为两个不同的平面,则下列四个命题中不正确的是 A. ,且,则 B. ,且,则 C. ,且,则 D. ,且,则 6.函数在区间上的零点个数为 ( ) A.2 B.3 C.4 D.5 7.下列命题中正确的是 ( ) A.若命题,则命题 B. “”是“直线与直线互相垂直”的充要条件 C. 若,则 D. 函数图像的一条对称轴是 8.执行如图所示的程序框图,则输出的结果为 A. 9 B. 11 C. 10 D. 7 9.刘徽是一个伟大的数学家,他的杰作九章算术注和海岛算经是中国最宝贵的文化遗产,他所提出的割圆术可以估算圆周率,理论上能把的值计算到任意的精度割圆术的第一步是求圆的内接正六边形的面积若在圆内随机取一点,则此点取自该圆内接正六边形的概率是( ) A. B. C. D. 10.如果椭圆的弦被点平分,那么这条弦所在的直线的方程是 A. B. C. D. 11.某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为a,b,且直线与以为圆心的圆交于B,C两点,且,则圆C的方程为 A. B. C. D. 12.设,分别是椭圆E:的左、右焦点,过点的直线交椭圆E于A,B两点,,若,则椭圆E的离心率为 A. B. C. D. 二.填空题:本大题共4小题,每小题5分,共20分. 13. 已知的面积,,则__ 14. 已知双曲线的左、右焦点分别为,,若双曲线上存在点P使,则离心率的取值范围是______ . 15.过点作圆的两条切线,与圆相切于A,B则直线AB的方程为________. 16.已知集合A是函数的定义域,集合B是不等式的解集:,q:.若是q的充分不必要条件,则a的取值范围是________. 三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分10分)已知圆C:,直线l过点P(-2,0) 若直线l与圆C相切,求直线l的方程; 当直线l与圆C相交于A,B两点,且时,求直线l的方程 18.(本小题满分10分)设,命题q:“方程表示双曲线”,命题p:,满足.Ⅰ若命题是真命题,求a的范围;Ⅱ为假,为真,求a的取值范围. 19.(本小题满分12分)直三棱柱中,,. (Ⅰ)证明; (Ⅱ)已知,,求三棱锥的体积. 20. (本小题满分12分)己知抛物线C:,过抛物线的焦点F且垂直于x轴的直线交抛物线于不同的两点A,B,且. 求抛物线C的方程; 若不经过坐标原点O的直线l与抛物线C相交于不同的两点M,N,且满足 证明直线l过x轴上一定点Q,并求出点Q的坐标. 21. (本小题满分12分)空气质量按照空气质量指数大小分为七档五级,相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大. 现统计天长市2018年10月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图. 求这60天中属轻度污染的天数; 求这60天空气质量指数的平均值 将频率分布直方图中的五组从左到右依次命名为第一组,第二组,,第五组从第一组和第五组中的所有天数中抽出两天,记它们的空气质量指数分别为x,y,求事件的概率. 22.(本小题满分14分)设椭圆的离心率为,左顶点到直线的距离为.Ⅰ求椭圆C的方程;Ⅱ设直线l与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;Ⅲ在Ⅱ的条件下,试求面积S的最小值. 答案 一.CADCBD DABCAC 二.13. 2 ; 14. ; 15. ; 16. . 三. 17.10分【答案】解:将圆C的方程配方得标准方程为,则此圆的圆心为,半径为2. 当直线l斜率不存在时方程为x=-2满足与圆C相切,;当直线l斜率存在时设l:.则有,;综上直线l的方程为x=-2或 。。。。5分 由(1)知直线斜率必存在,过圆心C作,则根据题意和圆的性质, ,或7. 故所求直线方程为或. 。。。。10分 18. 10分【答案】解:Ⅰ真,则或得;。。2分 q真,则,得, 。。。。2分 真,. 。。。。5分Ⅱ由为假,为真、q同时为假或同时为真, 若p假q假,则,, 。。。。7分 若p真q真,则, 。。。。9分 综上或. 。。。。10分 19. 12分【答案】(Ⅰ)如图,连结, 是直三棱柱,=, 平面,故. 又,四边形是正方形, ,又, 平面,故. 。。。。6分 (Ⅱ),,. 由(Ⅰ)知,平面, S△·=. 。。。。12分 20. 12分【答案】解:由己知A,B两点所在的直线方程为则,故. 抛物线C的方程为. .。。。。4 由题意,直线l不与y轴垂直,设直线l的方程为,,,联立, 消去x,得. ,,, .。。。6 ,,又,, . , 解得或而, 此时. 直线l的方程为, 。。。。10分 故直线l过定点. 。。。。12分 21. 12分【答案】解:依题意知,轻度污染即空气质量指数在之间,共有天. 。。。。3分 由直方图知60天空气质量指数的平均值为. 。 。。。7分 第一组和第五组的天数分别为天,天, 则从9天中抽出2天的一切可能结果的基本事件有36种, 由知两天只能在同一组中,而两天在同一组中的基本事件有18种, 用M表示这一事件,则概率. 。.。。。12分 22. 14分【答案】解:Ⅰ由已知, 因为 故所求椭圆的方程为 。。。。。。4分Ⅱ法一:设,, 当直线l的斜率不存在时,由椭圆对称性知,,因为以AB为直径的圆经过坐标原点O,故,即 又因为点在椭圆上,故,解得, 此时点O到直线AB的距离为 。。。。。。。6分 当直线l的斜率存在时,设其方程为l:. 联立得: 所以, 由已知,以AB为直径的圆经过坐标原点O,则,且 故 化简得, 故点O到直线AB的距离为 。。。。。。。 9分 综上,点O到直线AB的距离为定值 。。。。。。。10分 法二:若设直线方程为l:,也要对直线斜率为0进行讨论 设,, 当直线l的斜率为0时,由椭圆对称性知,,因为以AB为直径的圆经过坐标原点O,故,即 又因为点在椭圆上,故,解得, 此时点O到直线AB的距离为 当直线l的斜率不为0,或斜率不存在时,设其方程为l:. 联立得: 所以, 故, 即,所以, 所以, 化简得,故点O到直线AB的距离为 综上,点O到直线AB的距离为定值Ⅲ法一:当直线OA、直线OB中有一条斜率不存在,另一条斜率为0时,易知 当直线OA、直线OB斜率存在且不为0时,设直线OA的斜率为k, 则直线OB的斜率为,由得, 同理 故 令,则 故 综上,面积S的最小值为. 。。。。。。14分 法二:由Ⅱ,当直线l的斜率不存在时,, 当直线l的斜率存在时,,且点O到直线AB的距离为, 故 , 令,则, 因为,故. 综上,面积S的最小值为查看更多