【数学】安徽省滁州市定远县重点中学2020届高三6月模拟试题（理）（解析版）

【数学】安徽省滁州市定远县重点中学2020届高三6月模拟试题（理）（解析版）

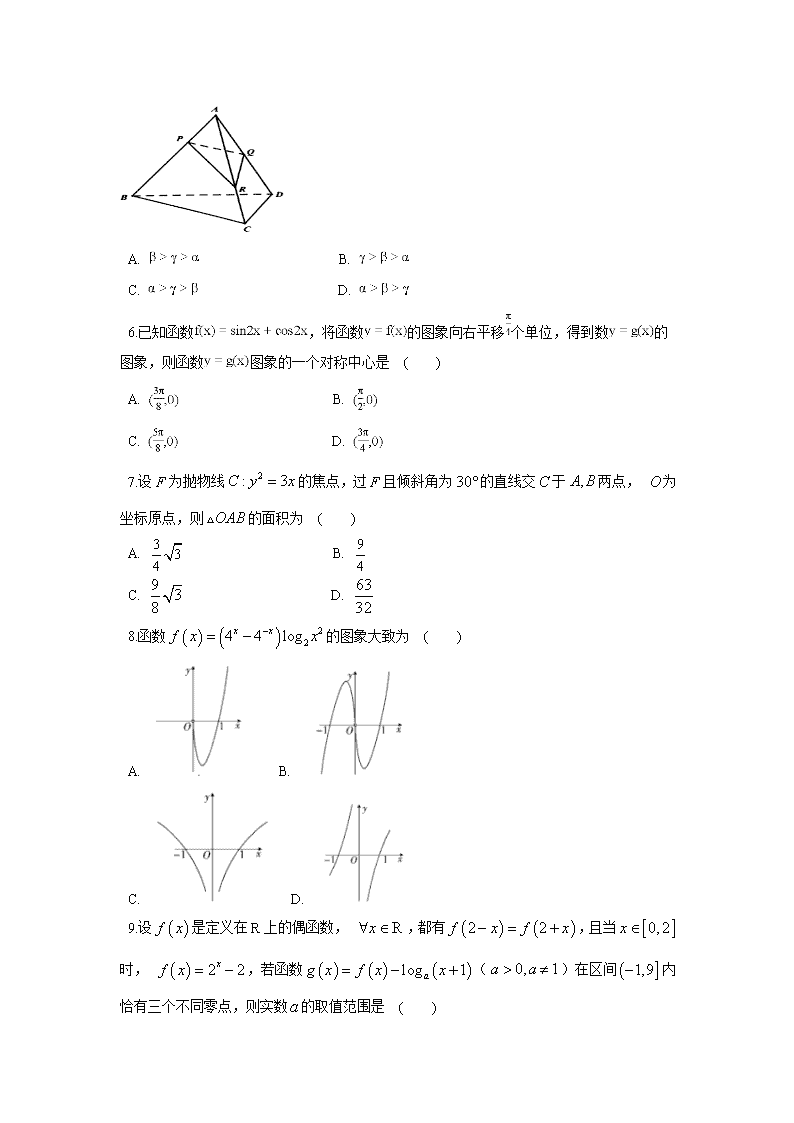
安徽省滁州市定远县重点中学2020届高三6月模拟 数学试题（理）‎ 第I卷 选择题（共60分）‎ 一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。) ‎ ‎1.设全集，集合，，则 ( )‎ A. B. ‎ C. D. ‎ ‎3.阅读如图所示程序框图，运行相应的程序.当输入的时，则输出的范围是 ( )‎ A. B. ‎ C. D. ‎ ‎4.已知为所在平面内一点， ， ，则的面积等于 ( )‎ A. B. ‎ C. D. ‎ ‎5.如图，正四面体中，、、在棱、、上，且，，分别记二面角，，的平面角为、、，在 ( )‎ A. B. ‎ C. D. ‎ ‎6.已知函数，将函数的图象向右平移个单位，得到数的图象，则函数图象的一个对称中心是 ( )‎ A. B. ‎ C. D. ‎ ‎7.设为抛物线的焦点，过且倾斜角为的直线交于两点， 为坐标原点，则的面积为 ( )‎ A. B. ‎ C. D. ‎ ‎8.函数的图象大致为 ( )‎ A. B. ‎ C. D. ‎ ‎9.设是定义在上的偶函数， ，都有，且当时， ，若函数（）在区间内恰有三个不同零点，则实数的取值范围是 ( )‎ A. B. ‎ C. D. ‎ ‎10.设函数，若存在区间，使在上的值域为，则的取值范围是( ) ‎ A. B. ‎ C. D. ‎ ‎11.已知是实数，若圆与直线相切，则的取值范围是 ( )‎ A. B. ‎ C. D. ‎ ‎12.下列说法正确的是 ( )‎ A. 若命题，，则，‎ B. 已知相关变量满足回归方程，若变量增加一个单位，则平均增加个单位 C. 命题“若圆与两坐标轴都有公共点，则实数”为真命题 D. 已知随机变量，若，则 第II卷 非选择题（共90分）‎ 本卷包括必考题和选考题两部分。第13题-第21题为必考题，每个试题考生都必须作答。第22题-第23题为选考题，考生根据要求作答。‎ 二、填空题(本大题共4小题,每小题5分,共20分) ‎ ‎13.若满足约束条件，则的最大值是__________．‎ ‎14.多项式 展开式中所有项的系数之和为64，则该展开式中的常数项为__________．‎ ‎15.《九章算术》第三章“衰分”中有如下问题：“今有甲持钱五百六十，乙持钱三百五十，丙持钱一百八十，凡三人俱出关，关税百钱，欲以钱数多少衰出之，问各几何？”其意为：“仅有甲带了560钱，乙带了350钱，丙带了180钱，三人一起出关，共需要交关税100钱，依照钱的多少按比例出钱”，则丙应出__________钱（所得结果四舍五入，保留整数）．‎ ‎16.已知函数对任意的，都有，函数是奇函数，当时， ，则方程在区间内的所有零点之和为_____________．‎ 三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。) ‎ ‎17. （本题12分）‎ 在△ABC中，角A、B、C所对的边分别为a、b、c，且.‎ ‎（1）求角C的大小；‎ ‎（2）若A=，△ABC的面积为，M为BC的中点，求AM.‎ ‎18. （本题12分）‎ ‎2012年12月18日，作为全国首批开展空气质量新标准监测的74个城市之一，郑州市正式发布数据.资料表明，近几年来，郑州市雾霾治理取得了很大成效，空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数（），其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点，以9个站点测得的的平均值为依据，播报我市的空气质量.‎ ‎（Ⅰ）若某日播报的为118，已知轻度污染区的平均值为74，中度污染区的平均值为114，求重度污染区的平均值；‎ ‎（Ⅱ）如图是2018年11月的30天中的分布，11月份仅有一天在内.‎ 组数 分组 天数 第一组 ‎3‎ 第二组 ‎4‎ 第三组 ‎4‎ 第四组 ‎6‎ 第五组 ‎5‎ 第六组 ‎4‎ 第七组 ‎3‎ 第八组 ‎1‎ ‎①郑州市某中学利用每周日的时间进行社会实践活动，以公布的为标准，如果小于180，则去进行社会实践活动.以统计数据中的频率为概率，求该校周日进行社会实践活动的概率；‎ ‎②在“创建文明城市”活动中，验收小组把郑州市的空气质量作为一个评价指标，从当月的空气质量监测数据中抽取3天的数据进行评价，设抽取到不小于180的天数为，求的分布列及数学期望.‎ ‎19. （本题12分）‎ 已知多面体中，四边形为平行四边形， ，且， ， ， .‎ ‎（1）求证：平面平面；‎ ‎（2）若，直线与平面夹角的正弦值为，求的值.‎ ‎20. （本题12分）‎ 已知椭圆：的右焦点为，且点在椭圆上．‎ ‎⑴求椭圆的标准方程；‎ ‎⑵已知动直线过点且与椭圆交于两点．试问轴上是否存在定点,使得恒成立？若存在，求出点Q的坐标；若不存在，请说明理由．‎ ‎21. （本题12分）‎ 已知函数.‎ ‎（1）当时，判断函数的单调性；‎ ‎（2）当有两个极值点时，若的极大值小于整数，求的最小值.‎ 请考生在第22、23题中任选一题作答。注意：只能做选定的题目，如果多做，则按所做的第一题计分，解答时请写清题号。‎ ‎22. [选修4-4：坐标系与参数方程]（本题10分）‎ 在直角坐标系中中，曲线的参数方程为为参数， ）. 以坐标原点为极点， 轴正半轴为极轴建立极坐标系，已知直线的极坐标方程为.‎ ‎（1）设是曲线上的一个动点，当时，求点到直线的距离的最大值；‎ ‎（2）若曲线上所有的点均在直线的右下方，求的取值范围.‎ ‎23.[选修4-5：不等式选讲]（本题10分）‎ 已知定义在上的函数，且恒成立.‎ ‎（1）求实数的值；‎ ‎（2）若，求证： .‎ 参考答案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C B D B D C B B A C B C ‎1.C【解析】 由题意得，‎ ‎∴，‎ ‎∴．选C．‎ ‎2.B【解析】由，‎ 得：，‎ 所以，，‎ 所以，故选：B．‎ ‎3.D【解析】当时，，‎ 则；‎ 当时，；‎ 综上所述，输出的范围为．‎ ‎4.B【解析】根据条件得知点P在三角形中位线的延长线上，三角形ABC是以B为直角的直角三角形，记AC中点为O点，OBPC按这一顺序构成平行四边形的四个边，并且是菱形，边长为2，故BC为2，此时三角形面积为 故答案为：B。‎ ‎5.D【解析】是正四面体，、、在棱、、上，且，，可得为钝角，为锐角，设到的距离为，到的距离为，到的距离为，到的距离为，设正四面体的高为 ,可得，由余弦定理可得 ，由三角形面积相等可得到，所以可以推出所以 ，故选D.‎ ‎6.C【解析】，‎ 将函数的图象向右平移个单位，得到数的图象，‎ 即，‎ 由，得，，‎ 当时，，‎ 即函数的一个对称中心为，故选：C．‎ ‎7.B【解析】由，得 则 ‎ ‎∴过的直线方程为 ‎ 即 ‎ 联立 ，得 ‎ 设 则 ‎ ‎ ‎ ‎ 故选B.‎ ‎8.B【解析】∵‎ ‎∴为奇函数，排除A，C，‎ ‎， ，且 排除D，故选：B ‎9.A【解析】由可得函数的图象关于对称，即 又函数是偶函数，则，‎ ‎∴，即函数的周期是4．‎ 当时， ，此时，‎ 由得，令 ‎．‎ ‎∵函数（）在区间内恰有三个不同零点，‎ ‎∴函数和的图象在区间内有三个不同的公共点．‎ 作出函数的图象如图所示．‎ ‎①当时，函数为增函数，‎ 结合图象可得，要使两函数的图象有三个公共点，则需满足在点A处的函数值小于2，在点B处的函数值大于2，‎ 即，解得；‎ ‎ ②当时，函数为减函数，‎ 结合图象可得，要使两函数的图象有三个公共点，则需满足在点C处的函数值小于，在点B处的函数值大于，‎ 即，解得．‎ 综上可得实数的取值范围是．选A．‎ ‎10.C【解析】详解：由题意，设，则 当时，，所以函数在单调递增，‎ 所以，所以在单调递增，‎ 因为，所以在单调递增，‎ 因为在上的值域为，所以，‎ 所以方程在上有两解，‎ 作出与直线的函数的图象，则两图象有两个交点，‎ 若直线过点，则，‎ 若直线与的图象相切，设切点为 则，解得，‎ 综上所述，所以实数的取值范围是，故选C.‎ ‎11.B【解析】11.由题设圆心到直线的距离，即，也即，因为，所以，即，解之得或，应选答案B。‎ ‎12.C【解析】若命题，，则，;‎ 已知相关变量满足回归方程，若变量增加一个单位，则平均减少个单位;‎ 命题“若圆与两坐标轴都有公共点，则 为真命题;‎ 已知随机变量，若，则;所以选C.‎ ‎13.‎ ‎【解析】,‎ 画出约束条件表示的可行域，如图，平移直线，当直线经过点 时，直线在 轴上的截距最小， 有最大值，由可得， 有最大值为 ，故答案为.‎ ‎14.141‎ ‎【解析】由展开式中所有项的系数之和为可得： ，则 展开式中的常数项可分为种情况 个括号都取 ‎⑵个括号取， 个括号取， 个括号都取，‎ ‎⑶个括号取， 个括号取， 个括号取，‎ ‎⑷个括号取， 个括号取，‎ 展开式中的常数项为 ‎15.17‎ ‎【解析】依照钱的多少按比例出钱，所以丙应该出钱，故填.‎ ‎16.4‎ ‎【解析】∵函数是奇函数 ‎∴函数的图象关于点对称 ‎∴把函数的图象向右平移1个单位可得函数的图象，即函数的图象关于点对称，则.‎ 又∵‎ ‎∴，从而 ‎∴，即 ‎∴函数的周期为2，且图象关于直线对称.‎ 画出函数的图象如图所示：‎ ‎ ‎ ‎∴结合图象可得区间内有8个零点，且所有零点之和为.‎ 故答案为4.‎ ‎17.(1) (2) .‎ ‎【解析】(1)∵‎ ‎ ∴‎ ‎ ∴‎ 由正弦定理得：即 ‎ ∴‎ ‎ ∵C为三角形的内角，∴‎ ‎(2)由（1）知，∴‎ ‎∴△ABC为等腰三角形，即CA=CB 又∵M为CB中点 ∴CM=BM 设CA=CB=2x则CM=BM=x ‎∴解得：x=2‎ ‎∴CA=4,CM=2‎ 由余弦定理得：AM=.‎ ‎18. （Ⅰ）设重度污染区的平均值为，则，解得.‎ 即重度污染区平均值为172.‎ ‎（Ⅱ）①由题意知，在内的天数为1，‎ 由图可知，在内的天数为17天，故11月份小于180的天数为，‎ 又，则该学校去进行社会实践活动的概率为.‎ ‎②由题意知，的所有可能取值为0，1，2，3，且 ‎，，‎ ‎，，‎ 则的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 数学期望 .‎ ‎19.解析：（1）∵， ，∴，‎ ‎∴；‎ 又， ，∴平面；‎ 因为平面，所以平面平面.‎ ‎（2）因为平面平面，平面平面， ，‎ 所以平面， 平面，故；‎ 以为原点， 所在直线分别为轴，过点且垂直于平面的直线为轴，建立如图所示的空间直角坐标系，‎ 设，则， ， ， ，‎ 设平面的一个法向量，‎ 因为， ，‎ ‎∴，取， ，则，‎ ‎，‎ 设直线与平面的夹角为，‎ 故，解得（舍去），故.‎ ‎20.（1）（2）轴上存在点 解析：（1）由题意知，‎ 根据椭圆的定义得：‎ 即 ‎，‎ 椭圆的标准方程为 ‎（2）假设在轴上存在点，使得恒成立．‎ ‎① 当直线的斜率为时，，．‎ 则 解得．‎ ‎② 当直线的斜率不存在时，，．‎ 则 解得或 ‎③ 由①②可知当直线的斜率为或不存在时，使得成立．‎ 下面证明即时恒成立．‎ 设直线的斜率存在且不为时，直线方程为，,‎ 由，可得 ‎，‎ ‎∴‎ 综上所述：在轴上存在点，使得恒成立．‎ ‎21.（1）为上的减函数（2）3‎ 详解：（1）由题.‎ 方法1：由于，‎ 又，所以，从而，‎ 于是为上的减函数.‎ 方法2：令，则，‎ 当时，，为增函数；当时，，为减函数.‎ 故在时取得极大值，也即为最大值.‎ 则.由于，所以，‎ 于是为上的减函数.‎ ‎（2）令，则，‎ 当时，，为增函数；当时，，为减函数.‎ 当趋近于时，趋近于.‎ 由于有两个极值点，所以有两个不等实根，‎ 即有两不等实根（）.‎ 则解得.‎ 可知，由于，，则.‎ 而，即（#）‎ 所以，于是，（*）‎ 令，则（*）可变为，‎ 可得，而，则有，‎ 下面再说明对于任意，.‎ 又由（#）得，把它代入（*）得，‎ 所以当， 恒成立，‎ 故为的减函数，所以.‎ 所以满足题意的整数的最小值为3.‎ ‎22.（1）（2）解：(1)由，‎ 得，化成直角坐标方程，得，‎ 即直线的方程为，依题意，设，则到直线的距离，当，即时， ，故点到直线的距离的最大值为.‎ ‎(2)因为曲线上的所有点均在直线的右下方， ‎ ‎ ， 恒成立，即 ‎（其中）恒成立， ，又，‎ 解得，故取值范围为.‎ ‎23. 解：（1）,要使恒成立，则，解得.又 ， .‎ ‎（2），‎ 即，当且仅当，即时取等号，故.‎