- 2021-06-23 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年河北省衡水中学四川分校·遂中实验校高高二上学期第一学段考试数学(文)试题(Word版)
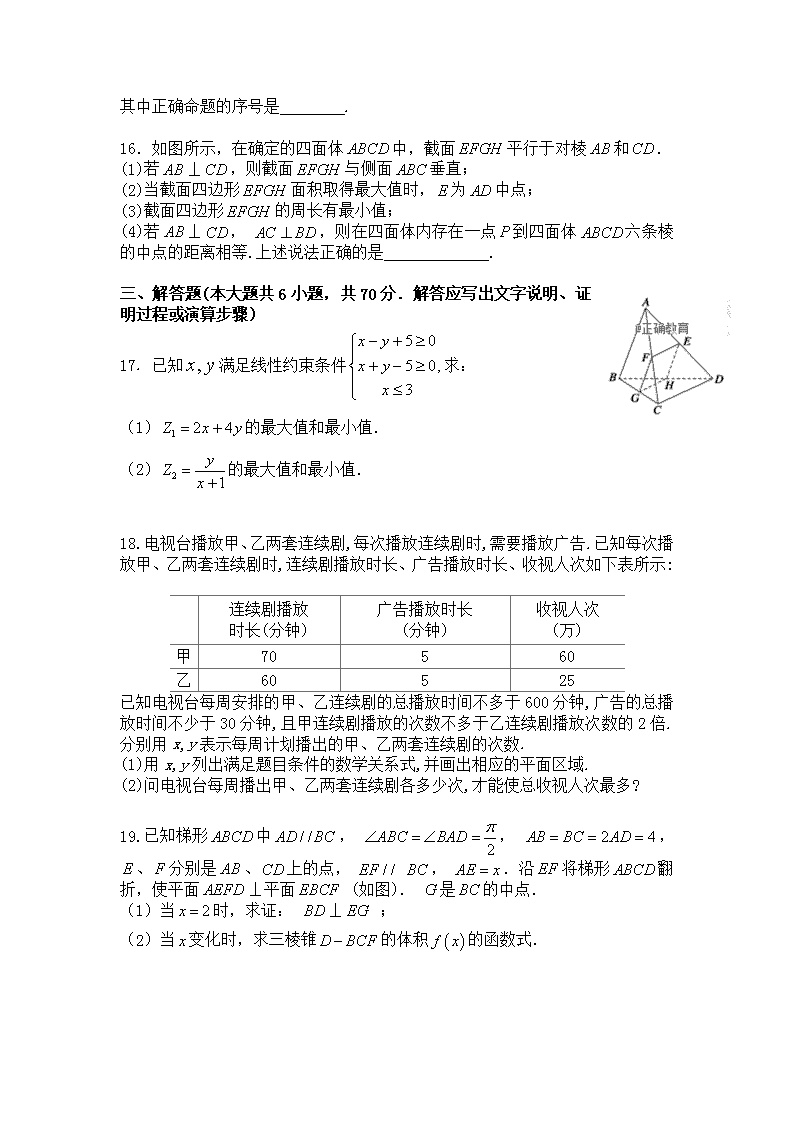
衡水中学四川分校·遂中实验校高2020届第三期第一学段考试 数学科试题(文科) 考试时间:120分钟 总分:150分 第I卷(选择题 共60分) 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列说法中正确的是 ( ) A. 平行于同一直线的两个平面平行 B. 垂直于同一直线的两个平面平行 C. 平行于同一平面的两条直线平行 D. 垂直于同一直线的两条直线平行 2.设,是不同的直线,,是不同的平面,下列命题中正确的是( ) A. 若,,,则 B. 若,,,则 C. 若,,,则 D. 若,,,则 3.如图所示,在正方体ABCD—A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( ) A. AC B. BD C. A1D D. A1D1 4.已知直线,当变化时,所有的直线恒过定点( ) A. B. C. D. 5.直线 的斜率和在轴上的截距分别是( ) A. B. C. D. 6. 设x,y满足约束条件则z=x-y的取值范围是( ) A.[-3,0] B.[-3,2] C.[0,2] D.[0,3] 7. 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是 ( ) A.17π B.18π C.20π D.28π 8.如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.( ) A.π B.π Cπ D.π 9.如图,空间四面体的每条边都等于1,点,分别是,的中点,则等于( ) A. B. C. D. 10.在正方体中,直线与平面所成角的正弦值为 A. B. C. D. 11.如图,在棱长为1的正方体中,点在线段上运动,则下列命题错误的是( ) A. 异面直线和所成的角为定值 B. 直线和平面平行 C. 三棱锥的体积为定值 D. 直线和平面所成的角为定值 12.如图,矩形中, 为边的中点,将绕直线翻转成不在平面内),若分别为线段的中点,则在翻转过程中,下列说法错误的是( ) A. 与平面垂直的直线必与直线BM垂直 B.一定存在某个位置,使 C. 异面直线与所成角是定值 D. 三棱锥外接球半径与棱的长之比为定值 第II卷(非选择题 共90分) 二、填空题(本大题共4个小题,每小题5分,共20分) 13.直线与直线互相平行,则实数________. 14.正方体中,异面直线与所成角的大小为________. 15.给出下列命题: ①有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱; ②四棱锥的四个侧面都可以是直角三角形; ③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥; ④棱台的上、下底面可以不相似,但侧棱长一定相等. 其中正确命题的序号是 . 16.如图所示,在确定的四面体中,截面平行于对棱和. (1)若⊥,则截面与侧面垂直; (2)当截面四边形面积取得最大值时,为中点; (3)截面四边形的周长有最小值; (4)若⊥,,则在四面体内存在一点到四面体六条棱的中点的距离相等.上述说法正确的是 . 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17. 已知满足线性约束条件求: (1)的最大值和最小值. (2)的最大值和最小值. 18.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示: 连续剧播放 时长(分钟) 广告播放时长 (分钟) 收视人次 (万) 甲 70 5 60 乙 60 5 25 已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数. (1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域. (2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多? 19.已知梯形中, , , 、分别是、上的点, , .沿将梯形翻折,使平面⊥平面 (如图). 是的中点. (1)当时,求证: ⊥ ; (2)当变化时,求三棱锥的体积的函数式. 20.如图,在斜三棱柱中,已知,,且. (Ⅰ)求证:平面平面; (Ⅱ)若,求四棱锥的体积. 21.如图,菱形的边长为,,,将菱形沿对角线折起,得到三棱锥,点是棱的中点,. ()求证:平面. ()求证:平面平面. ()求三棱锥的体积. 22.已知点(x,y)是区域内的点,目标函数z=x+y,z的最大值记作,若数列的前n项和为,,且点在直线上. (Ⅰ)证明:数列为等比数列; (Ⅱ)求数列的前n项和Tn. 衡水中学四川分校·遂中实验校高2020届第三期第一学段考试 数学科试题(文科)参考答案 1-5:BCBBA 6-10:BADAD 11-12:DB 13.,14.,15②,16.②④ 17.【解析】(1)线性约束条件表示的平面区域为及内部(如上图),可得.,则表示直线在轴上的截距的倍,显然当直线过点C时最小,过点B时最大,所以. (2),则表示点与点连线的斜率,显然点在点C时取得最小值,在点D时取得最大值且. 18.解:(1)由已知,x,y满足的数学关系式为即 该二元一次不等式组所表示的平面区域为图中的阴影部分. (2)设总收视人次为z万,则目标函数为z=60x+25y. 考虑z=60x+25y,将它变形为y=-x+,这是斜率为-,随z变化的一族平行直线. 为直线在y轴上的截距,当取得最大值时,z的值最大. 又因为x,y满足约束条件,所以由图可知,当直线z=60x+25y经过可行域上的点M时,截距最大,即z最大. 解方程组 得点M的坐标为(6,3). 所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多 19.【解析】(1)证明:作,垂足,连结, , ∵平面平面,交线, 平面, ∴平面,又平面,故. ∵, , . ∴四边形为正方形,故. 又、平面,且,故平面.又平面,故. (2)解:∵,平面平面,交线, 平面. ∴面.又由(1)平面,故, ∴四边形是矩形, ,故以、、、为顶点的三棱锥的高. 又. ∴三棱锥的体积 20.【解析】(1)证明:连接,在平行四边形中, 由得平行四边形为菱形,所以, 又,所以,所以, 又,所以,所以平面平面 (2)取的中点O,连接AO,易知平面,平面, 所以点到平面的距离为,由平面,所以点到平面的距离为,点到平面的距离为. . 故四棱锥的体积为. 21.【解析】()证明:∵点是菱形的对角线交点,∴是的中点, 又∵点是棱的中点,∴是的中位线,, ∵平面,平面,∴平面. ()证明:由题意,∵,∴,, 又∵菱形中,,,∴平面, ∵平面,∴平面平面. ()∵三棱锥的体积等于三棱锥的体积由()知平面, ∴是三棱锥的高, ,∴. 22.【答案】(Ⅰ)证明见解析(Ⅱ),(n∈N*) 【解析】试题分析:(Ⅰ)作出可行域,由目标函数可得当,时,取得最大值,且最大值为,又点在直线上,则,即,则,由可得当时,,即,得证;(Ⅱ)由(Ⅰ)得,可知数列为等差数列与等比数列之和,可用分组求和法求. 试题解析:解:(Ⅰ)∵目标函数对应直线l:z=x+y, 区域,(n∈N*)表示以x轴、y轴和直线x+2y=2n为三边的三角形, ∴当x=2n,y=0时,z的最大值zn=2n ∵(Sn,an)在直线zn=x+y上 ∴zn=Sn+an,可得Sn=2n﹣an, 当n≥2时,可得an=Sn﹣Sn﹣1=(2n﹣an)﹣[2(n﹣1)﹣an﹣1] 化简整理,得2an=an﹣1+2 因此,an﹣2=(an﹣1+2)﹣2=(an﹣1﹣2) 当n=1时,an﹣2=a1﹣2=﹣1 ∴数列{an﹣2}是以﹣1为首项,公比q=的等比数列; (Ⅱ)由(I)得an﹣2=﹣()n﹣1, ∴an=2﹣()n﹣1,可得Sn=2n﹣an=2n﹣2+()n﹣1, ∴根据等差数列和等比数列的求和公式,得 即数列{Sn}的前n项和Tn=,(n∈N*).查看更多