专题03 导数与应用-备战2018高考高三数学（文）全国各地优质模拟试卷分项精品

专题03 导数与应用-备战2018高考高三数学（文）全国各地优质模拟试卷分项精品

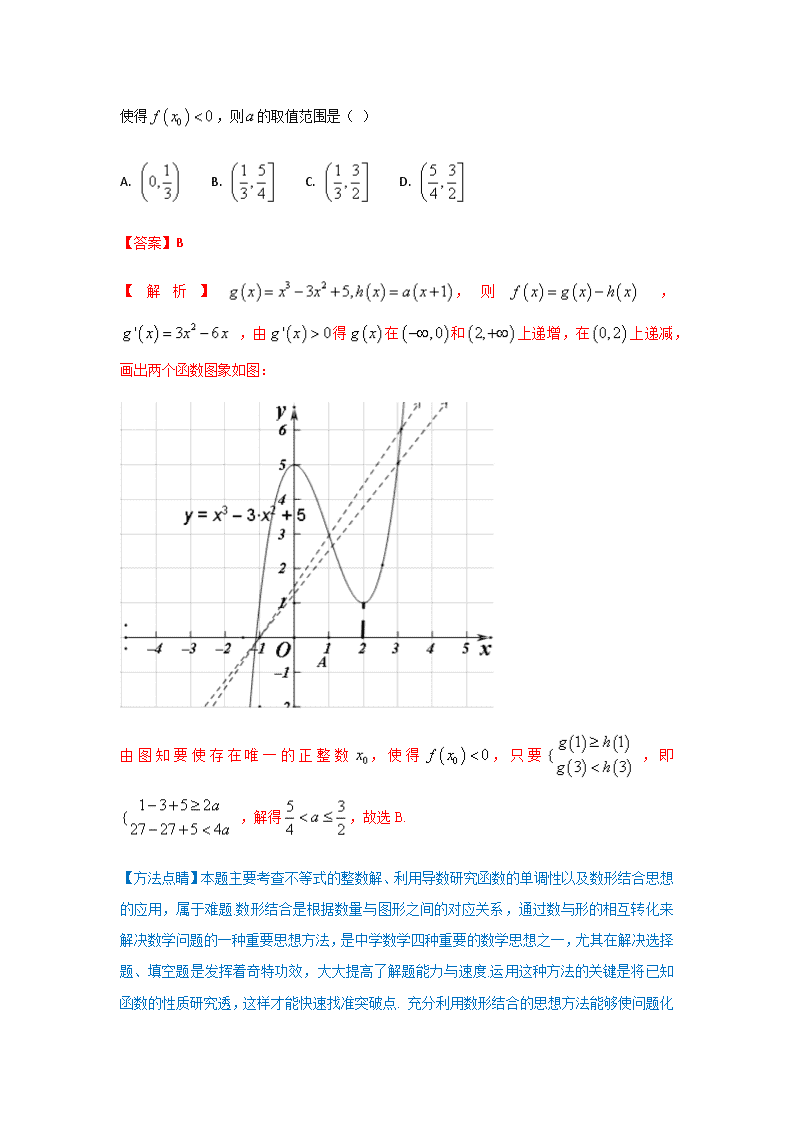
一、选择题 ‎1．【2018湖南永州市一模】已知定义在上的可导函数的导函数为，若对于任意实数有，且，则不等式的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎2．【2018河南中原名校质检二】已知函数，则的极大值为（ ）‎ A. 2 B. C. D. ‎ ‎【答案】B ‎【解析】，则,令x=1得，所以 则，所以函数在（0,2）上递增，在（2，+）上递减，‎ 则的极大值为 故选B ‎ ‎3．【2018湖南两市高三调研】设函数，若存在唯一的正整数 ‎，使得，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】，则 ， ，由得在和上递增，在上递减，画出两个函数图象如图：‎ 由图知要使存在唯一的正整数，使得，只要，即，解得，故选B. ‎ ‎【方法点睛】本题主要考查不等式的整数解、利用导数研究函数的单调性以及数形结合思想的应用，属于难题.数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决选择题、填空题是发挥着奇特功效，大大提高了解题能力与速度.运用这种方法的关键是将已知函数的性质研究透，这样才能快速找准突破点. ‎ 充分利用数形结合的思想方法能够使问题化难为简，并迎刃而解.‎ ‎4．【2018吉林百校联盟九月联考】已知关于的不等式有唯一整数解，则实数的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】A 故选：A ‎ 点睛：不等式有唯一整数解问题可以转化为两个图像的位置关系问题，观察与的图象的高低关系，只要保证上方只有一个整数满足即可.‎ ‎5．【2018广东珠海市高三摸底】已知函数恰有两个零点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎6．【2018超级全能生九月联考】已知函数有三个零点，则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】显然不满足三个零点，所以， ，当时， （）两图像必有一交点，所以必有一零点在。当x>0时， 所以f(x)在单调递减，在上单调递增。上要有两个零点，只需，解得，选D. ‎ ‎【点睛】‎ 零点问题，常把方程F(x)=0变形为左右两边各放一个函数f(x)=g(x),然后分别出来 y=f(x)和y=g(x)的图像，再观察两图像交点个数，从而得到y=F(x)的零点个数。如果图像不好直接画出，则要借助导数及函数图像来解决。‎ ‎7．【2018贵州遵义航天高级中学一模】曲线: 在点处的切线方程为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】 ，所以切线方程为 ，选C.‎ ‎8．【2018黔东南州一模】若函数有两个零点，则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎ ‎ 由得，此时函数单调递减，即当时，函数取得极小值，当时，∴要使函数有两个零点，即方程有两个不同的根，即函数和有两个不同的交点，则， 故选C. ‎ 点睛：本题主要考查函数零点的应用，构造函数求函数的导数，利用函数极值和导数之间的关系是解决本题的关键；根据函数零点的定义， ，得，设函数，利用导数研究函数的极值即可得到结论.‎ 二、填空题 ‎9．【2018河北武邑中学调研二】若函数的图象在处的切线方程是，则__________．‎ ‎【答案】-1‎ ‎10．【2018衡水金卷高三联考】已知函数，若曲线在点处的切线经过圆：的圆心，则实数的值为__________．‎ ‎【答案】‎ ‎【解析】对求导，得，所以.‎ 故所求切线的方程为，即.‎ 由该直线经过圆：的圆心，得.解得.‎ ‎11．【2018河南南阳一中三模】经过原点作函数图象的切线，则切线方程为__________．‎ ‎【答案】‎ ‎12．【2018广东珠海六校联考】若曲线上点处的切线平行于直线，则点的坐标是________.‎ ‎【答案】‎ ‎【解析】试题分析：设切点 ，则由得： ，所以点的坐标是. ‎ 考点：利用导数求切点.‎ ‎13．【2018超级全能生联考】已知函数在区间上既有极大值又有极小值，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】，由题意可得在有两个不等根，即 在有两个不等根，所以，解得，填 ‎ ‎14．【2018贵州遵义航天高级中学一模】已知，若存在，使得，则实数的取值范围是______‎ ‎【答案】‎ ‎【解析】 ，所以 ‎ 点睛：(1)运用函数图象解决问题时，先要正确理解和把握函数图象本身的含义及其表示的内容，熟悉图象所能够表达的函数的性质.‎ ‎(2)在研究函数性质特别是单调性、最值、零点时，要注意用好其与图象的关系，结合图象研究.‎ ‎15．【2018黑龙江省哈尔滨九中二模】设函数.其中，存在使得成立，则实数的值为__________．‎ ‎【答案】‎ ‎，则，根据题意，要使，则，此时恰好为垂足，由，解得. ‎ ‎【方法点睛】本题主要考查了导数在研究函数最值中的应用，考查了转化的数学思想，属于中档题.把函数看作动点与动点之间距离的平方，利用导数求出曲线上与直线平行的切线的切点，得到曲线上点到直线的距离的最小值，结合题意可得只有切点到直线距离的平方等于，然后由两直线斜率的关系式求得实数的值.‎ ‎16．【2018山西一模】若函数的单调递减区间为，则__________．‎ ‎【解析】，由题知是方程的解，故.‎ 三、解答题 ‎17．【2018河北武邑中学质检二】已知函数的图象过点.‎ ‎（1）求函数的单调增区间；‎ ‎（2）若函数有3个零点，求的取值范围.‎ ‎【答案】(1) 函数的递增区间是， (2) ‎ 所以函数的递增区间是， .‎ ‎（2）由（1）知 ，‎ 同理， ，‎ 由数形结合思想，要使函数有三个零点，‎ 则，解得.‎ 所以的取值范围为. ‎ 点睛：已知函数有零点求参数取值范围常用的方法和思路 ‎(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；‎ ‎(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；‎ ‎(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．‎ ‎18．【2018河北武邑中学质检二】已知函数的图象在点处的切线方程为.‎ ‎（1）求的值；‎ ‎（2）求函数在上的最大值.‎ ‎【答案】(1) ， (2) ‎ ‎（2）由（1）知.‎ 因为，由，得，‎ 由得， ，‎ 所以函数在上递减，在上递增.‎ 因为， ，所以.‎ ‎19．【2018衡水金卷高三大联考】已知函数，.‎ ‎（1）求函数的单调区间；‎ ‎（2）若关于的方程有实数根，求实数的取值范围.‎ ‎【答案】（1）函数的单调递增区间为，单调递减区间为；（2）当时，方程有实数根.‎ 当时，，随的变化情况如下表：‎ 所以为函数的极小值，也是最小值.‎ 当，即时，函数没有零点；‎ 当，即时，注意到，‎ ‎，‎ 所以函数存在零点.‎ 综上所述，当时，方程有实数根.‎ 点睛：已知函数有零点求参数常用的方法和思路：‎ ‎（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；‎ ‎（2）分离参数法：先将参数分离，转化成函数的值域问题解决；‎ ‎（3）数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.‎ ‎20．【2018河南南阳一中三模】设函数.‎ ‎（1）当时，在上恒成立，求实数的取值范围；‎ ‎（2）当时，若函数在上恰有两个不同的零点，求实数的取值范围；‎ ‎【答案】（1）；（2）.‎ ‎（2）当时，函数，‎ 在上恰有两个不同的零点，即在上恰有两个不同的零点，‎ 令，则，‎ 当，；当，，‎ ‎∴在上单减，在上单增，，‎ 又，如图所示，‎ 所以实数的取值范围为(]【来.源：全,品…中&高*考*网】‎ 点睛：根据函数零点求参数取值，也是高考经常涉及的重点问题，‎ ‎（1）利用零点存在的判定定理构建不等式求解；‎ ‎（2）分离参数后转化为函数的值域（最值）问题求解，如果涉及由几个零点时，还需考虑函数的图象与参数的交点个数；‎ ‎（3）转化为两熟悉的函数图象的上、下关系问题，从而构建不等式求解.‎ ‎21．【2018河南南阳一中三模】已知函数.‎ ‎（1）若曲线在处的切线方程为，求实数和的值；‎ ‎（2）讨论函数的单调性.‎ ‎【答案】（1），b=-4；（2）在上是增函数，在上是减函数.‎ ‎22．【2018湖南永州市一模】已知函数，，其中为自然对数的底数.‎ ‎（1）讨论函数在区间上的单调性；‎ ‎（2）已知，若对任意，有，求实数的取值范围.‎ ‎【答案】（1）见解析；（2）‎ ‎（2），依题意，时，恒成立.已知，则当时，，在上单调递减，而在上单调递增，，‎ ‎，得，当时，，与在上均单调递增，，，，得与矛盾，综上所述，实数的取值范围是 点睛：本题考查导数知识的运用，考查函数的单调性，由，得函数单调递增，得函数单调递减；考查恒成立问题，正确分离参数是关键，也是常用的一种手段．通过分离参数可转化为或恒成立，即或即可，利用导数知识结合单调性求出或即得解.‎ ‎23．【2018河南中原名校质检二】已知函数.‎ ‎（1）若在处的切线是，求实数的值；‎ ‎（2）当时，函数有且仅有一个零点，若此时，恒成立，求实数的取值范围.‎ ‎【答案】（1）（2）‎ ‎（2）由已知（）‎ 即方程（）有唯一的实数根 所以（）‎ 即直线与函数（）的图象有唯一的交点 构造函数 （）‎ ‎（）‎ 令，，‎ 而，∴；，，；，，‎ ‎∴，；，且，；，‎ 所以 已知可化为（）的最小值 ‎（）‎ 所以在上减，在上增 所以 综上实数的取值范围是 点睛：函数有几个零点的问题可采用变量分离转化为两个函数图像的交点，构造新函数研究单调性，图像得恒成立的问题转化为.‎ ‎24．【2018湖南两市九月调研】已知函数.‎ ‎（1）当时，求曲线在点处的切线方程；‎ ‎（2）若有两个零点，求的取值范围.‎ ‎【答案】(1) ；(2) ．‎ 设方程的两个根分别为，则，‎ 令得，其中，‎ 所以函数在上递增，在上递减.‎ ‎①当时，显然在上单调递增，至多一个零点，不符合题意；‎ ‎②当时，函数在上递增，在上递减，‎ 要使有两个零点，必须，即，‎ 又由得：，代入上面的不等式得：‎ ‎，解得 下面证明：当时，有两个零点.‎ ‎，‎ 又，‎ 且，‎ ‎，‎ 所以在与上各有一个零点.‎ ‎【方法点晴】本题主要考查利用导数求曲线切线方程、利用导数研究函数的单调性与零点，属于难题.求曲线切线方程的一般步骤是：（1）求出在处的导数，即 在点 出的切线斜率（当曲线在处的切线与轴平行时，在 处导数不存在，切线方程为）；（2）由点斜式求得切线方程.‎ ‎25．【2018吉林百校联盟九月联考】已知函数， ．‎ ‎（1）求函数的单调递增区间；‎ ‎（2）若， ，且， ， ，求实数的取值范围．‎ ‎【答案】(1) 函数的单调递增区间为;(2) .‎ ‎①当时，∵,∴，∴恒成立，‎ ‎∴在上单调递增， ，‎ 故在上恒成立，符合题意．　【来.源：全,品…中&高*考*网】‎ ‎②当时，令，得，令，得，【来.源：全,品…中&高*考*网】‎ 故在上单调递减，所以，‎ 而，设函数， ，‎ 则，令，则（）恒成立，‎ ‎∴在上单调递增，∴恒成立，‎ ‎∴在上单调递增，∴ 恒成立，‎ 即，而，不合题意．　‎ 综上，故实数的取值范围为.‎ ‎26．【2018辽宁沈阳市育才学校一模】已知函数， （为自然对数的底数）.‎ ‎ (Ⅰ)讨论的单调性；‎ ‎ (Ⅱ)当时，不等式恒成立，求实数的值.‎ ‎【答案】（Ⅰ）当时， 在上为减函数；当时，则在上为减函数；在上为增函数；（Ⅱ） .‎ ‎ (Ⅱ) ， ‎ 由于不等式恒成立，说明的最小值为，‎ 当 时， 说明；下面验证：‎ 当时，由(Ⅰ)可知： 在上为减函数； 在上为增函数；‎ ‎ 当时， 有最小值，即有.故适合题意. ‎ ‎【点睛】利用导数研究函数的单调性首先求出函数的导数，令导数为零，解出，划分区间研究导数的正负，给出单调区间和单调性，有参数要对参数分类进行讨论；不等式恒成立的基本解法是分离参数，利用极值原理解决，但本题提供最值并易于发现极值点，所以较简单一些.‎ ‎27．【2018广东珠海市高三摸底】已知函数.‎ ‎（1）讨论的单调性；‎ ‎（2）若，求的取值范围.‎ ‎【答案】(1) 当时， 在上单调递增，当时， 在上单调递增，在上单调递减；（2）.‎ ‎（2）由得： ，‎ 当时， ，满足题意； ‎ 当时，设， ‎ 在上单调递增， ，不合题意；‎ 当时，令得，‎ 令得 ‎，则， 【来.源：全,品…中&高*考*网】‎ 综上所述， 的取值范围为. ‎ ‎28．【2018吉林长春市一模】已知函数．‎ ‎（Ⅰ）若函数的图像与直线相切，求的值；‎ ‎（Ⅱ）若恒成立，求整数的最大值． 【来.源：全,品…中&高*考*网】‎ ‎【答案】（1）1（2）2‎ ‎29．【2018贵州遵义航天高级中学一模】已知函数.‎ ‎(1)求函数的单调区间 ‎(2)若存在,使得成立,求的取值范围.‎ ‎【答案】(1)当 a≤﹣1时，f（x）在（0，+∞）上是增函数，当a＞﹣1时，在（0，1+a）上是减函数，在（1+a，+∞）上是增函数；(2) （﹣∞，﹣2）∪（，+∞）.‎ ‎②当1+a＞0，即a＞﹣1时，‎ x∈（0，1+a）时，f′（x）＜0；x∈（1+a，+∞）时，f′（x）＞0；‎ 故f（x）在（0，1+a）上是减函数，在（1+a，+∞）上是增函数；‎ ‎（2）①当a≤﹣1时，‎ 存在x0∈[1，e]（e=2.718…），使得f（x0）＜0成立可化为 f（1）=1+1+a＜0，‎ 解得，a＜﹣2；‎ ‎②当﹣1＜a≤0时，‎ 存在x0∈[1，e]（e=2.718…），使得f（x0）＜0成立可化为 f（1）=1+1+a＜0，解得，a＜﹣2；‎ ‎③当0＜a≤e﹣1时，‎ 存在x0∈[1，e]（e=2.718…），使得f（x0）＜0成立可化为 f（1+a）=1+a﹣aln（1+a）+1＜0，无解；‎ ‎④当e﹣1＜a时，‎ ‎ ‎