2016年全国统一高考数学试卷（文科）（新课标ⅱ）

2016年全国统一高考数学试卷（文科）（新课标ⅱ）

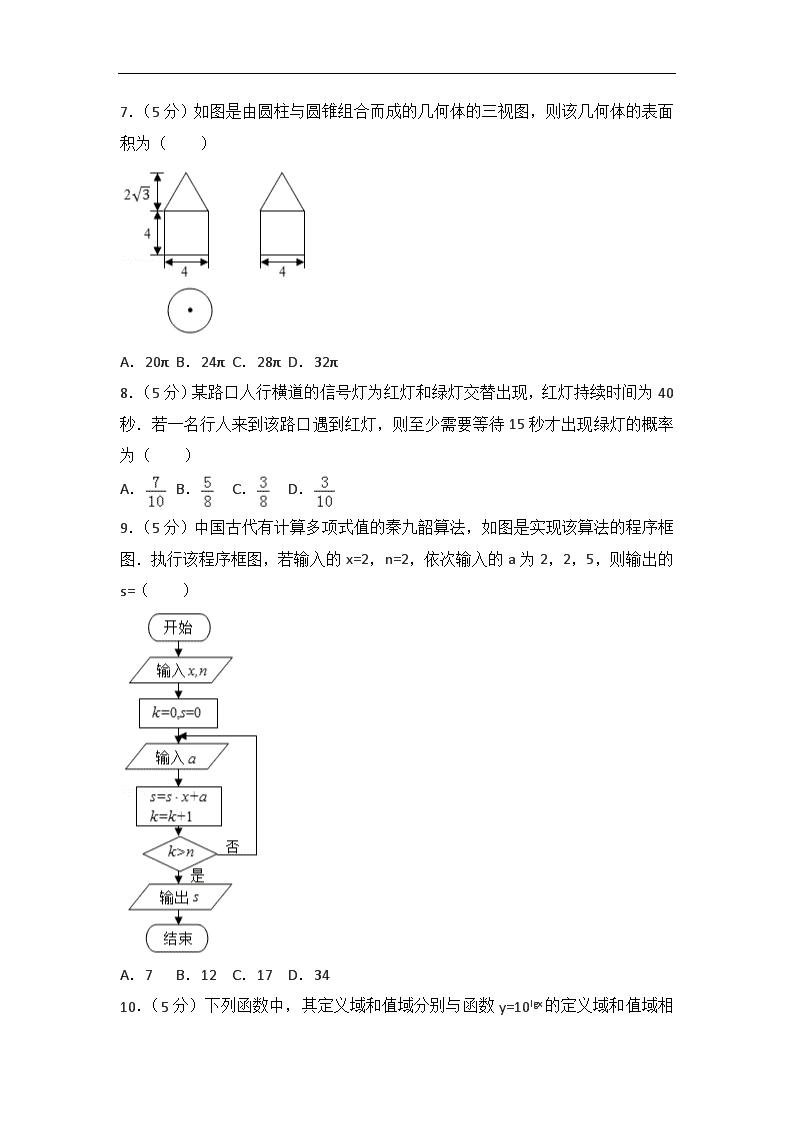
‎2016年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出四个选项，只有一个选项符合题目要求.‎ ‎1．（5分）已知集合A={1，2，3}，B={x|x2＜9}，则A∩B=（　　）‎ A．{﹣2，﹣1，0，1，2，3} B．{﹣2，﹣1，0，1，2}‎ C．{1，2，3} D．{1，2}‎ ‎2．（5分）设复数z满足z+i=3﹣i，则=（　　）‎ A．﹣1+2i B．1﹣2i C．3+2i D．3﹣2i ‎3．（5分）函数y=Asin（ωx+φ）的部分图象如图所示，则（　　）‎ A．y=2sin（2x﹣） B．y=2sin（2x﹣） C．y=2sin（x+） D．y=2sin（x+）‎ ‎4．（5分）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为（　　）‎ A．12π B．π C．8π D．4π ‎5．（5分）设F为抛物线C：y2=4x的焦点，曲线y=（k＞0）与C交于点P，PF⊥x轴，则k=（　　）‎ A． B．1 C． D．2‎ ‎6．（5分）圆x2+y2﹣2x﹣8y+13=0的圆心到直线ax+y﹣1=0的距离为1，则a=（　　）‎ A．﹣ B．﹣ C． D．2‎ ‎7．（5分）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（　　）‎ A．20π B．24π C．28π D．32π ‎8．（5分）某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒．若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为（　　）‎ A． B． C． D．‎ ‎9．（5分）中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=2，n=2，依次输入的a为2，2，5，则输出的s=（　　）‎ A．7 B．12 C．17 D．34‎ ‎10．（5分）下列函数中，其定义域和值域分别与函数y=10lgx 的定义域和值域相同的是（　　）‎ A．y=x B．y=lgx C．y=2x D．y=‎ ‎11．（5分）函数f（x）=cos2x+6cos（﹣x）的最大值为（　　）‎ A．4 B．5 C．6 D．7‎ ‎12．（5分）已知函数f（x）（x∈R）满足f（x）=f（2﹣x），若函数y=|x2﹣2x﹣3|与 y=f（x） 图象的交点为（x1，y1），（x2，y2），…，（xm，ym），则xi=（　　）‎ A．0 B．m C．2m D．4m ‎　‎ 二、填空题：本题共4小题，每小题5分.‎ ‎13．（5分）已知向量=（m，4），=（3，﹣2），且∥，则m=　 　．‎ ‎14．（5分）若x，y满足约束条件，则z=x﹣2y的最小值为　 　．‎ ‎15．（5分）△ABC的内角A，B，C的对边分别为a，b，c，若cosA=，cosC=，a=1，则b=　 　．‎ ‎16．（5分）有三张卡片，分别写有1和2，1和3，2和3．甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是　 　．‎ ‎　‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤.‎ ‎17．（12分）等差数列{an}中，a3+a4=4，a5+a7=6．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．‎ ‎18．（12分）某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 保费 ‎0.85a a ‎1.25a ‎1.5a ‎1.75a ‎2a 随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：‎ 出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 频数 ‎60‎ ‎50‎ ‎30‎ ‎30‎ ‎20‎ ‎10‎ ‎（I）记A为事件：“一续保人本年度的保费不高于基本保费”．求P（A）的估计值；‎ ‎（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”．求P（B）的估计值；‎ ‎（Ⅲ）求续保人本年度的平均保费估计值．‎ ‎19．（12分）如图，菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，CD上，AE=CF，EF交BD于点H，将△DEF沿EF折到△D′EF的位置．‎ ‎（Ⅰ）证明：AC⊥HD′；‎ ‎（Ⅱ）若AB=5，AC=6，AE=，OD′=2，求五棱锥D′﹣ABCFE体积．‎ ‎20．（12分）已知函数f（x）=（x+1）lnx﹣a（x﹣1）．‎ ‎（I）当a=4时，求曲线y=f（x）在（1，f（1））处的切线方程；‎ ‎（II）若当x∈（1，+∞）时，f（x）＞0，求a的取值范围．‎ ‎21．（12分）已知A是椭圆E：+=1的左顶点，斜率为k（k＞0）的直线交E于A，M两点，点N在E上，MA⊥NA．‎ ‎（I）当|AM|=|AN|时，求△AMN的面积 ‎（II） 当2|AM|=|AN|时，证明：＜k＜2．‎ ‎　‎ 请考生在第22～24题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-1：几何证明选讲]‎ ‎22．（10分）如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F．‎ ‎（Ⅰ）证明：B，C，G，F四点共圆；‎ ‎（Ⅱ）若AB=1，E为DA的中点，求四边形BCGF的面积．‎ ‎　‎ ‎[选项4-4：坐标系与参数方程]‎ ‎23．在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25．‎ ‎（Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；‎ ‎（Ⅱ）直线l的参数方程是（t为参数），l与C交与A，B两点，|AB|=，求l的斜率．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．已知函数f（x）=|x﹣|+|x+|，M为不等式f（x）＜2的解集．‎ ‎（Ⅰ）求M；‎ ‎（Ⅱ）证明：当a，b∈M时，|a+b|＜|1+ab|．‎ ‎　‎ ‎2016年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出四个选项，只有一个选项符合题目要求.‎ ‎1．（5分）已知集合A={1，2，3}，B={x|x2＜9}，则A∩B=（　　）‎ A．{﹣2，﹣1，0，1，2，3} B．{﹣2，﹣1，0，1，2}‎ C．{1，2，3} D．{1，2}‎ ‎【分析】先求出集合A和B，由此利用交集的定义能求出A∩B的值．‎ ‎【解答】解：∵集合A={1，2，3}，B={x|x2＜9}={x|﹣3＜x＜3}，‎ ‎∴A∩B={1，2}．‎ 故选：D．‎ ‎【点评】本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．‎ ‎　‎ ‎2．（5分）设复数z满足z+i=3﹣i，则=（　　）‎ A．﹣1+2i B．1﹣2i C．3+2i D．3﹣2i ‎【分析】根据已知求出复数z，结合共轭复数的定义，可得答案．‎ ‎【解答】解：∵复数z满足z+i=3﹣i，‎ ‎∴z=3﹣2i，‎ ‎∴=3+2i，‎ 故选：C．‎ ‎【点评】本题考查的知识点是复数代数形式的加减运算，共轭复数的定义，难度不大，属于基础题．‎ ‎　‎ ‎3．（5分）函数y=Asin（ωx+φ）的部分图象如图所示，则（　　）‎ A．y=2sin（2x﹣） B．y=2sin（2x﹣） C．y=2sin（x+） D．y=2sin（x+）‎ ‎【分析】根据已知中的函数y=Asin（ωx+φ）的部分图象，求出满足条件的A，ω，φ值，可得答案．‎ ‎【解答】解：由图可得：函数的最大值为2，最小值为﹣2，故A=2，‎ ‎=，故T=π，ω=2，‎ 故y=2sin（2x+φ），‎ 将（，2）代入可得：2sin（+φ）=2，‎ 则φ=﹣满足要求，‎ 故y=2sin（2x﹣），‎ 故选：A．‎ ‎【点评】本题考查的知识点是由y=Asin（ωx+φ）的部分图象确定其解析式，确定各个参数的值是解答的关键．‎ ‎　‎ ‎4．（5分）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为（　　）‎ A．12π B．π C．8π D．4π ‎【分析】先通过正方体的体积，求出正方体的棱长，然后求出球的半径，即可求出球的表面积．‎ ‎【解答】解：正方体体积为8，可知其边长为2，‎ 正方体的体对角线为=2，‎ 即为球的直径，所以半径为，‎ 所以球的表面积为=12π．‎ 故选：A．‎ ‎【点评】本题考查学生的空间想象能力，体积与面积的计算能力，是基础题．‎ ‎　‎ ‎5．（5分）设F为抛物线C：y2=4x的焦点，曲线y=（k＞0）与C交于点P，PF⊥x轴，则k=（　　）‎ A． B．1 C． D．2‎ ‎【分析】根据已知，结合抛物线的性质，求出P点坐标，再由反比例函数的性质，可得k值．‎ ‎【解答】解：抛物线C：y2=4x的焦点F为（1，0），‎ 曲线y=（k＞0）与C交于点P在第一象限，‎ 由PF⊥x轴得：P点横坐标为1，‎ 代入C得：P点纵坐标为2，‎ 故k=2，‎ 故选：D．‎ ‎【点评】本题考查的知识点是抛物线的简单性质，反比例函数的性质，难度中档．‎ ‎　‎ ‎6．（5分）圆x2+y2﹣2x﹣8y+13=0的圆心到直线ax+y﹣1=0的距离为1，则a=（　　）‎ A．﹣ B．﹣ C． D．2‎ ‎【分析】求出圆心坐标，代入点到直线距离方程，解得答案．‎ ‎【解答】解：圆x2+y2﹣2x﹣8y+13=0的圆心坐标为：（1，4），‎ 故圆心到直线ax+y﹣1=0的距离d==1，‎ 解得：a=，‎ 故选：A．‎ ‎【点评】本题考查的知识点是圆的一般方程，点到直线的距离公式，难度中档．‎ ‎　‎ ‎7．（5分）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（　　）‎ A．20π B．24π C．28π D．32π ‎【分析】空间几何体是一个组合体，上面是一个圆锥，圆锥的底面直径是4，圆锥的高是2，在轴截面中圆锥的母线长使用勾股定理做出的，写出表面积，下面是一个圆柱，圆柱的底面直径是4，圆柱的高是4，做出圆柱的表面积，注意不包括重合的平面．‎ ‎【解答】解：由三视图知，空间几何体是一个组合体，‎ 上面是一个圆锥，圆锥的底面直径是4，圆锥的高是2，‎ ‎∴在轴截面中圆锥的母线长是=4，‎ ‎∴圆锥的侧面积是π×2×4=8π，‎ 下面是一个圆柱，圆柱的底面直径是4，圆柱的高是4，‎ ‎∴圆柱表现出来的表面积是π×22+2π×2×4=20π ‎∴空间组合体的表面积是28π，‎ 故选：C．‎ ‎【点评】本题考查由三视图求表面积，本题的图形结构比较简单，易错点可能是两个几何体重叠的部分忘记去掉，求表面积就有这样的弊端．‎ ‎　‎ ‎8．（5分）某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒．若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为（　　）‎ A． B． C． D．‎ ‎【分析】求出一名行人前25秒来到该路口遇到红灯，即可求出至少需要等待15秒才出现绿灯的概率．‎ ‎【解答】解：∵红灯持续时间为40秒，至少需要等待15秒才出现绿灯，‎ ‎∴一名行人前25秒来到该路口遇到红灯，‎ ‎∴至少需要等待15秒才出现绿灯的概率为=．‎ 故选：B．‎ ‎【点评】本题考查概率的计算，考查几何概型，考查学生的计算能力，比较基础．‎ ‎　‎ ‎9．（5分）中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=2，n=2，依次输入的a为2，2，5，则输出的s=（　　）‎ A．7 B．12 C．17 D．34‎ ‎【分析】根据已知的程序框图可得，该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，可得答案．‎ ‎【解答】解：∵输入的x=2，n=2，‎ 当输入的a为2时，S=2，k=1，不满足退出循环的条件；‎ 当再次输入的a为2时，S=6，k=2，不满足退出循环的条件；‎ 当输入的a为5时，S=17，k=3，满足退出循环的条件；‎ 故输出的S值为17，‎ 故选：C．‎ ‎【点评】本题考查的知识点是程序框图，当循环次数不多，或有规律可循时，可采用模拟程序法进行解答．‎ ‎　‎ ‎10．（5分）下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（　　）‎ A．y=x B．y=lgx C．y=2x D．y=‎ ‎【分析】分别求出各个函数的定义域和值域，比较后可得答案．‎ ‎【解答】解：函数y=10lgx的定义域和值域均为（0，+∞），‎ 函数y=x的定义域和值域均为R，不满足要求；‎ 函数y=lgx的定义域为（0，+∞），值域为R，不满足要求；‎ 函数y=2x的定义域为R，值域为（0，+∞），不满足要求；‎ 函数y=的定义域和值域均为（0，+∞），满足要求；‎ 故选：D．‎ ‎【点评】本题考查的知识点是函数的定义域和值域，熟练掌握各种基本初等函数的定义域和值域，是解答的关键．‎ ‎　‎ ‎11．（5分）函数f（x）=cos2x+6cos（﹣x）的最大值为（　　）‎ A．4 B．5 C．6 D．7‎ ‎【分析】运用二倍角的余弦公式和诱导公式，可得y=1﹣2sin2x+6sinx，令t=sinx（﹣1≤t≤1），可得函数y=﹣2t2+6t+1，配方，结合二次函数的最值的求法，以及正弦函数的值域即可得到所求最大值．‎ ‎【解答】解：函数f（x）=cos2x+6cos（﹣x）‎ ‎=1﹣2sin2x+6sinx，‎ 令t=sinx（﹣1≤t≤1），‎ 可得函数y=﹣2t2+6t+1‎ ‎=﹣2（t﹣）2+，‎ 由∉[﹣1，1]，可得函数在[﹣1，1]递增，‎ 即有t=1即x=2kπ+，k∈Z时，函数取得最大值5．‎ 故选：B．‎ ‎【点评】本题考查三角函数的最值的求法，注意运用二倍角公式和诱导公式，同时考查可化为二次函数的最值的求法，属于中档题．‎ ‎　‎ ‎12．（5分）已知函数f（x）（x∈R）满足f（x）=f（2﹣x），若函数y=|x2﹣2x﹣3|与 y=f（x） 图象的交点为（x1，y1），（x2，y2），…，（xm，ym），则xi=（　　）‎ A．0 B．m C．2m D．4m ‎【分析】根据已知中函数函数f（x）（x∈R）满足f（x）=f（2﹣x），分析函数的对称性，可得函数y=|x2﹣2x﹣3|与 y=f（x） 图象的交点关于直线x=1对称，进而得到答案．‎ ‎【解答】解：∵函数f（x）（x∈R）满足f（x）=f（2﹣x），‎ 故函数f（x）的图象关于直线x=1对称，‎ 函数y=|x2﹣2x﹣3|的图象也关于直线x=1对称，‎ 故函数y=|x2﹣2x﹣3|与 y=f（x） 图象的交点也关于直线x=1对称，‎ 故xi=×2=m，‎ 故选：B．‎ ‎【点评】‎ 本题考查的知识点是二次函数的图象和性质，函数的对称性质，难度中档．‎ ‎　‎ 二、填空题：本题共4小题，每小题5分.‎ ‎13．（5分）已知向量=（m，4），=（3，﹣2），且∥，则m=　﹣6　．‎ ‎【分析】直接利用向量共线的充要条件列出方程求解即可．‎ ‎【解答】解：向量=（m，4），=（3，﹣2），且∥，‎ 可得12=﹣2m，解得m=﹣6．‎ 故答案为：﹣6．‎ ‎【点评】本题考查向量共线的充要条件的应用，考查计算能力．‎ ‎　‎ ‎14．（5分）若x，y满足约束条件，则z=x﹣2y的最小值为　﹣5　．‎ ‎【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 联立，解得B（3，4）．‎ 化目标函数z=x﹣2y为y=x﹣z，‎ 由图可知，当直线y=x﹣z过B（3，4）时，直线在y轴上的截距最大，z有最小值为：3﹣2×4=﹣5．‎ 故答案为：﹣5．‎ ‎【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．‎ ‎　‎ ‎15．（5分）△ABC的内角A，B，C的对边分别为a，b，c，若cosA=，cosC=，a=1，则b=　　．‎ ‎【分析】运用同角的平方关系可得sinA，sinC，再由诱导公式和两角和的正弦公式，可得sinB，运用正弦定理可得b=，代入计算即可得到所求值．‎ ‎【解答】解：由cosA=，cosC=，可得 sinA===，‎ sinC===，‎ sinB=sin（A+C）=sinAcosC+cosAsinC=×+×=，‎ 由正弦定理可得b=‎ ‎==．‎ 故答案为：．‎ ‎【点评】本题考查正弦定理的运用，同时考查两角和的正弦公式和诱导公式，以及同角的平方关系的运用，考查运算能力，属于中档题．‎ ‎　‎ ‎16．（5分）有三张卡片，分别写有1和2，1和3，2和3．甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是　1和3　．‎ ‎【分析】可先根据丙的说法推出丙的卡片上写着1和2，或1和3，分别讨论这两种情况，根据甲和乙的说法可分别推出甲和乙卡片上的数字，这样便可判断出甲卡片上的数字是多少．‎ ‎【解答】解：根据丙的说法知，丙的卡片上写着1和2，或1和3；‎ ‎（1）若丙的卡片上写着1和2，根据乙的说法知，乙的卡片上写着2和3；‎ ‎∴根据甲的说法知，甲的卡片上写着1和3；‎ ‎（2）若丙的卡片上写着1和3，根据乙的说法知，乙的卡片上写着2和3；‎ 又甲说，“我与乙的卡片上相同的数字不是2”；‎ ‎∴甲的卡片上写的数字不是1和2，这与已知矛盾；‎ ‎∴甲的卡片上的数字是1和3．‎ 故答案为：1和3．‎ ‎【点评】考查进行简单的合情推理的能力，以及分类讨论得到解题思想，做这类题注意找出解题的突破口．‎ ‎　‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤.‎ ‎17．（12分）等差数列{an}中，a3+a4=4，a5+a7=6．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．‎ ‎【分析】（Ⅰ）设等差数列{an}的公差为d，根据已知构造关于首项和公差方程组，解得答案；‎ ‎（Ⅱ）根据bn=[an]，列出数列{bn}的前10项，相加可得答案．‎ ‎【解答】解：（Ⅰ）设等差数列{an}的公差为d，‎ ‎∵a3+a4=4，a5+a7=6．‎ ‎∴，‎ 解得：，‎ ‎∴an=；‎ ‎（Ⅱ）∵bn=[an]，‎ ‎∴b1=b2=b3=1，‎ b4=b5=2，‎ b6=b7=b8=3，‎ b9=b10=4．‎ 故数列{bn}的前10项和S10=3×1+2×2+3×3+2×4=24．‎ ‎【点评】本题考查的知识点是等差数列的通项公式，等差数列的性质，难度中档．‎ ‎　‎ ‎18．（12分）某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 保费 ‎0.85a a ‎1.25a ‎1.5a ‎1.75a ‎2a 随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：‎ 出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 频数 ‎60‎ ‎50‎ ‎30‎ ‎30‎ ‎20‎ ‎10‎ ‎（I）记A为事件：“一续保人本年度的保费不高于基本保费”．求P（A）的估计值；‎ ‎（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”．求P（B）的估计值；‎ ‎（Ⅲ）求续保人本年度的平均保费估计值．‎ ‎【分析】‎ ‎（I）求出A为事件：“一续保人本年度的保费不高于基本保费”的人数．总事件人数，即可求P（A）的估计值；‎ ‎（Ⅱ）求出B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”的人数．然后求P（B）的估计值；‎ ‎（Ⅲ）利用人数与保费乘积的和除以总续保人数，可得本年度的平均保费估计值．‎ ‎【解答】解：（I）记A为事件：“一续保人本年度的保费不高于基本保费”．事件A的人数为：60+50=110，该险种的200名续保，‎ P（A）的估计值为：=；‎ ‎（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”．事件B的人数为：30+30=60，P（B）的估计值为：=；‎ ‎（Ⅲ）续保人本年度的平均保费估计值为==1.1925a．‎ ‎【点评】本题考查样本估计总体的实际应用，考查计算能力．‎ ‎　‎ ‎19．（12分）如图，菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，CD上，AE=CF，EF交BD于点H，将△DEF沿EF折到△D′EF的位置．‎ ‎（Ⅰ）证明：AC⊥HD′；‎ ‎（Ⅱ）若AB=5，AC=6，AE=，OD′=2，求五棱锥D′﹣ABCFE体积．‎ ‎【分析】（1）根据直线平行的性质以菱形对角线垂直的性质进行证明即可．‎ ‎（2）根据条件求出底面五边形的面积，结合平行线段的性质证明OD′是五棱锥D′﹣ABCFE的高，即可得到结论．‎ ‎【解答】（Ⅰ）证明：∵菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，CD上，AE=CF，‎ ‎∴EF∥AC，且EF⊥BD 将△DEF沿EF折到△D′EF的位置，‎ 则D′H⊥EF，‎ ‎∵EF∥AC，‎ ‎∴AC⊥HD′；‎ ‎（Ⅱ）若AB=5，AC=6，则AO=3，B0=OD=4，‎ ‎∵AE=，AD=AB=5，‎ ‎∴DE=5﹣=，‎ ‎∵EF∥AC，‎ ‎∴====，‎ ‎∴EH=，EF=2EH=，DH=3，OH=4﹣3=1，‎ ‎∵HD′=DH=3，OD′=2，‎ ‎∴满足HD′2=OD′2+OH2，‎ 则△OHD′为直角三角形，且OD′⊥OH，‎ 又OD′⊥AC，AC∩OH=O，‎ 即OD′⊥底面ABCD，‎ 即OD′是五棱锥D′﹣ABCFE的高．‎ 底面五边形的面积S=+=+=12+=，‎ 则五棱锥D′﹣ABCFE体积V=S•OD′=××2=．‎ ‎【点评】本题主要考查空间直线和平面的位置关系的判断，以及空间几何体的体积，根据线面垂直的判定定理以及五棱锥的体积公式是解决本题的关键．本题的难点在于证明OD′是五棱锥D′﹣ABCFE的高．考查学生的运算和推理能力．‎ ‎　‎ ‎20．（12分）已知函数f（x）=（x+1）lnx﹣a（x﹣1）．‎ ‎（I）当a=4时，求曲线y=f（x）在（1，f（1））处的切线方程；‎ ‎（II）若当x∈（1，+∞）时，f（x）＞0，求a的取值范围．‎ ‎【分析】（I）当a=4时，求出曲线y=f（x）在（1，f（1））处的切线的斜率，即可求出切线方程；‎ ‎（II）先求出f′（x）＞f′（1）=2﹣a，再结合条件，分类讨论，即可求a的取值范围．‎ ‎【解答】解：（I）当a=4时，f（x）=（x+1）lnx﹣4（x﹣1）．‎ f（1）=0，即点为（1，0），‎ 函数的导数f′（x）=lnx+（x+1）•﹣4，‎ 则f′（1）=ln1+2﹣4=2﹣4=﹣2，‎ 即函数的切线斜率k=f′（1）=﹣2，‎ 则曲线y=f（x）在（1，0）处的切线方程为y=﹣2（x﹣1）=﹣2x+2；‎ ‎（II）∵f（x）=（x+1）lnx﹣a（x﹣1），‎ ‎∴f′（x）=1++lnx﹣a，‎ ‎∴f″（x）=，‎ ‎∵x＞1，∴f″（x）＞0，‎ ‎∴f′（x）在（1，+∞）上单调递增，‎ ‎∴f′（x）＞f′（1）=2﹣a．‎ ‎①a≤2，f′（x）＞f′（1）≥0，‎ ‎∴f（x）在（1，+∞）上单调递增，‎ ‎∴f（x）＞f（1）=0，满足题意；‎ ‎②a＞2，存在x0∈（1，+∞），f′（x0）=0，函数f（x）在（1，x0）上单调递减，在（x0，+∞）上单调递增，‎ 由f（1）=0，可得存在x0∈（1，+∞），f（x0）＜0，不合题意．‎ 综上所述，a≤2．‎ 另解：若当x∈（1，+∞）时，f（x）＞0，‎ 可得（x+1）lnx﹣a（x﹣1）＞0，‎ 即为a＜，‎ 由y=的导数为y′=，‎ 由y=x﹣﹣2lnx的导数为y′=1+﹣=＞0，‎ 函数y在x＞1递增，可得＞0，‎ 则函数y=在x＞1递增，‎ 则==2，‎ 可得＞2恒成立，‎ 即有a≤2．‎ ‎【点评】本题主要考查了导数的应用，函数的导数与函数的单调性的关系的应用，导数的几何意义，考查参数范围的求解，考查学生分析解决问题的能力，有难度．‎ ‎　‎ ‎21．（12分）已知A是椭圆E：+=1的左顶点，斜率为k（k＞0）的直线交E于A，M两点，点N在E上，MA⊥NA．‎ ‎（I）当|AM|=|AN|时，求△AMN的面积 ‎（II） 当2|AM|=|AN|时，证明：＜k＜2．‎ ‎【分析】（I）依题意知椭圆E的左顶点A（﹣2，0），由|AM|=|AN|，且MA⊥NA，可知△AMN为等腰直角三角形，设M（a﹣2，a），利用点M在E上，可得3（a﹣2）2+4a2=12，解得：a=，从而可求△AMN的面积；‎ ‎（II）设直线lAM的方程为：y=k（x+2），直线lAN的方程为：y=﹣（x+2），联立消去y，得（3+4k2）x2+16k2x+16k2﹣12=0，利用韦达定理及弦长公式可分别求得|AM|=|xM﹣（﹣2）|=，|AN|==，‎ 结合2|AM|=|AN|，可得=，整理后，构造函数f（k）=4k3﹣6k2+3k﹣8，利用导数法可判断其单调性，再结合零点存在定理即可证得结论成立．‎ ‎【解答】解：（I）由椭圆E的方程：+=1知，其左顶点A（﹣2，0），‎ ‎∵|AM|=|AN|，且MA⊥NA，∴△AMN为等腰直角三角形，‎ ‎∴MN⊥x轴，设M的纵坐标为a，则M（a﹣2，a），‎ ‎∵点M在E上，∴3（a﹣2）2+4a2=12，整理得：7a2﹣12a=0，∴a=或a=0（舍），‎ ‎∴S△AMN=a×2a=a2=；‎ ‎（II）设直线lAM的方程为：y=k（x+2），直线lAN的方程为：y=﹣（x+2），由 消去y得：（3+4k2）x2+16k2x+16k2﹣12=0，∴xM﹣2=﹣，∴xM=2﹣=，‎ ‎∴|AM|=|xM﹣（﹣2）|=•=‎ ‎∵k＞0，‎ ‎∴|AN|==，‎ 又∵2|AM|=|AN|，∴=，‎ 整理得：4k3﹣6k2+3k﹣8=0，‎ 设f（k）=4k3﹣6k2+3k﹣8，‎ 则f′（k）=12k2﹣12k+3=3（2k﹣1）2≥0，‎ ‎∴f（k）=4k3﹣6k2+3k﹣8为（0，+∞）的增函数，‎ 又f（）=4×3﹣6×3+3﹣8=15﹣26=﹣＜0，f（2）=4×8﹣6×4+3×2﹣8=6＞0，‎ ‎∴＜k＜2．‎ ‎【点评】本题考查直线与圆锥曲线的综合问题，常用的方法就是联立方程求出交点的横坐标或者纵坐标的关系，通过这两个关系的变形去求解，考查构造函数思想与导数法判断函数单调性，再结合零点存在定理确定参数范围，是难题．‎ ‎　‎ 请考生在第22～24题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-1：几何证明选讲]‎ ‎22．（10分）如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F．‎ ‎（Ⅰ）证明：B，C，G，F四点共圆；‎ ‎（Ⅱ）若AB=1，E为DA的中点，求四边形BCGF的面积．‎ ‎【分析】（Ⅰ）证明B，C，G，F四点共圆可证明四边形BCGF对角互补，由已知条件可知∠BCD=90°，因此问题可转化为证明∠GFB=90°；‎ ‎（Ⅱ）在Rt△DFC中，GF=CD=GC，因此可得△GFB≌△GCB，则S四边形BCGF=2S△BCG，据此解答．‎ ‎【解答】（Ⅰ）证明：∵DF⊥CE，‎ ‎∴Rt△DFC∽Rt△EDC，‎ ‎∴=，‎ ‎∵DE=DG，CD=BC，‎ ‎∴=，‎ 又∵∠GDF=∠DEF=∠BCF，‎ ‎∴△GDF∽△BCF，‎ ‎∴∠CFB=∠DFG，‎ ‎∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°，‎ ‎∴∠GFB+∠GCB=180°，‎ ‎∴B，C，G，F四点共圆．‎ ‎（Ⅱ）∵E为AD中点，AB=1，∴DG=CG=DE=，‎ ‎∴在Rt△DFC中，GF=CD=GC，连接GB，Rt△BCG≌Rt△BFG，‎ ‎∴S四边形BCGF=2S△BCG=2××1×=．‎ ‎【点评】本题考查四点共圆的判断，主要根据对角互补进行判断，注意三角形相似和全等性质的应用．‎ ‎　‎ ‎[选项4-4：坐标系与参数方程]‎ ‎23．在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25．‎ ‎（Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；‎ ‎（Ⅱ）直线l的参数方程是（t为参数），l与C交与A，B两点，|AB|=，求l的斜率．‎ ‎【分析】（Ⅰ）把圆C的标准方程化为一般方程，由此利用ρ2=x2+y2，x=ρcosα，y=ρsinα，能求出圆C的极坐标方程．‎ ‎（Ⅱ）由直线l的参数方程求出直线l的一般方程，再求出圆心到直线距离，由此能求出直线l的斜率．‎ ‎【解答】解：（Ⅰ）∵圆C的方程为（x+6）2+y2=25，‎ ‎∴x2+y2+12x+11=0，‎ ‎∵ρ2=x2+y2，x=ρcosα，y=ρsinα，‎ ‎∴C的极坐标方程为ρ2+12ρcosα+11=0．‎ ‎（Ⅱ）∵直线l的参数方程是（t为参数），‎ ‎∴t=，代入y=tsinα，得：直线l的一般方程y=tanα•x，‎ ‎∵l与C交与A，B两点，|AB|=，圆C的圆心C（﹣6，0），半径r=5，‎ 圆心到直线的距离d=．‎ ‎∴圆心C（﹣6，0）到直线距离d==，‎ 解得tan2α=，∴tanα=±=±．‎ ‎∴l的斜率k=±．‎ ‎【点评】本题考查圆的极坐标方程的求法，考查直线的斜率的求法，是中档题，解题时要认真审题，注意点到直线公式、圆的性质的合理运用．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．已知函数f（x）=|x﹣|+|x+|，M为不等式f（x）＜2的解集．‎ ‎（Ⅰ）求M；‎ ‎（Ⅱ）证明：当a，b∈M时，|a+b|＜|1+ab|．‎ ‎【分析】（I）分当x＜时，当≤x≤时，当x＞时三种情况，分别求解不等式，综合可得答案；‎ ‎（Ⅱ）当a，b∈M时，（a2﹣1）（b2﹣1）＞0，即a2b2+1＞a2+b2，配方后，可证得结论．‎ ‎【解答】解：（I）当x＜时，不等式f（x）＜2可化为：﹣x﹣x﹣＜2，‎ 解得：x＞﹣1，‎ ‎∴﹣1＜x＜，‎ 当≤x≤时，不等式f（x）＜2可化为：﹣x+x+=1＜2，‎ 此时不等式恒成立，‎ ‎∴≤x≤，‎ 当x＞时，不等式f（x）＜2可化为：﹣+x+x+＜2，‎ 解得：x＜1，‎ ‎∴＜x＜1，‎ 综上可得：M=（﹣1，1）；‎ 证明：（Ⅱ）当a，b∈M时，‎ ‎（a2﹣1）（b2﹣1）＞0，‎ 即a2b2+1＞a2+b2，‎ 即a2b2+1+2ab＞a2+b2+2ab，‎ 即（ab+1）2＞（a+b）2，‎ 即|a+b|＜|1+ab|．‎ ‎【点评】‎ 本题考查的知识点是绝对值不等式的解法，不等式的证明，难度中档．‎ ‎　‎