高中数学选修第3章3_1_2同步练习

高中数学选修第3章3_1_2同步练习

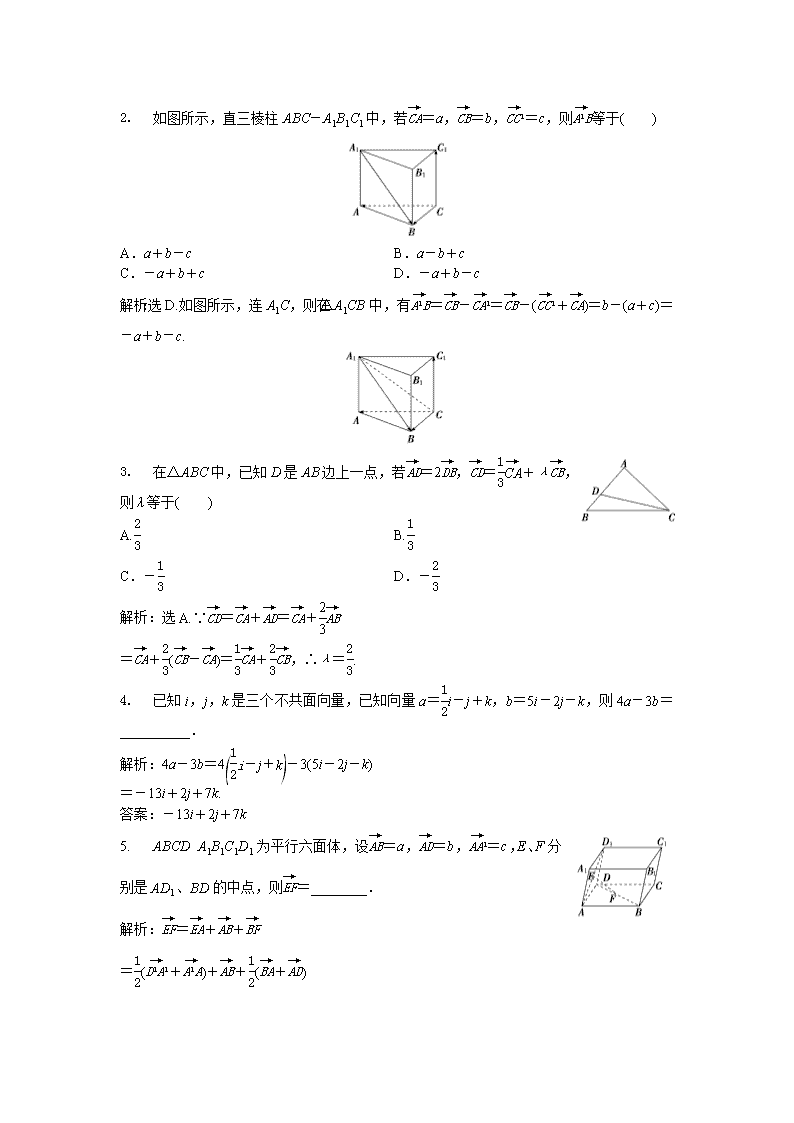
高中数学人教A版选2-1 同步练习 设a，b是不共线的两个向量，λ，μ∈R，且λa＋μ b＝0，则(　　)‎ A．λ＝μ＝0　　　　　　　　　 B．a＝b＝0‎ C．λ＝0，b＝0 D．μ＝0，a＝0‎ 解析：选A.∵a，b不共线，‎ ‎∴a，b为非零向量，又∵λa＋μ b＝0，‎ ‎∴λ＝μ＝0.‎ 已知点M在平面ABC内，并且对空间任一点O，＝x＋＋，则x的值为(　　)‎ A. B. C. D．0‎ 解析：选A.由四点共面的充要条件知，‎ x＋＋＝1，因此x＝.‎ 化简(a＋2b－‎3c)＋5－3(a－2b＋c)＝__________．‎ 答案：a＋b－c 非零向量e1，e2不共线，使ke1＋e2与e1＋ke2共线的k＝________．‎ 解析：若ke1＋e2与e1＋ke2共线，‎ 则ke1＋e2＝λ(e1＋ke2)，‎ ‎∴∴k＝±1.‎ 答案：±1‎ ‎[A级　基础达标]‎ 若a、b是平面α内的两个向量，则(　　)‎ A．α内任一向量p＝λa＋μb(λ，μ∈R)‎ B．若存在λ，μ∈R使λa＋μb＝0，则λ＝μ＝0‎ C．若a、b不共线，则空间任一向量p＝λa＋μb(λ，μ∈R)‎ D．若a、b不共线，则α内任一向量p＝λa＋μb(λ，μ∈R)‎ 解析：选D.当a与b是共线向量时，A不正确；当a与b是相反向量，λ＝μ≠0时，λa＋μb＝0，故B不正确；若a、b不共线，则平面α内的向量都可用a、b表示，对空间向量不行，故C不正确，D正确，故选D.‎ 如图所示，直三棱柱ABC－A1B‎1C1中，若＝a，＝b，＝c，则等于(　　)‎ A．a＋b－c B．a－b＋c C．－a＋b＋c D．－a＋b－c 解析：选D.如图所示，连A‎1C，则在△A1CB中，有＝－＝－(＋)＝b－(a＋c)＝－a＋b－c.‎ 在△ABC中，已知D是AB边上一点，若＝2，＝＋λ，则λ等于(　　)‎ A. B. C．－ D．－ 解析：选A.∵＝＋＝＋ ‎＝＋(－)＝＋，∴λ＝.‎ 已知i，j，k是三个不共面向量，已知向量a＝i－j＋k，b＝5i－2j－k，则‎4a－3b＝__________．‎ 解析：‎4a－3b＝4－3(5i－2j－k)‎ ‎＝－13i＋2j＋7k.‎ 答案：－13i＋2j＋7k ABCDA1B‎1C1D1为平行六面体，设＝a，＝b，＝c，E、F分别是AD1、BD的中点，则＝________．‎ 解析：＝＋＋ ‎＝(＋)＋＋(＋)‎ ‎＝(－b－c)＋a＋(－a＋b)＝a－c.‎ 答案：a－c 已知e1，e2是不共线向量，a＝3e1＋4e2，b＝－3e1＋8e2，判断a与b是否共线．‎ 解：设a＝λb，‎ 即3e1＋4e2＝λ(－3e1＋8e2)＝－3λe1＋8λe2，‎ ‎∴⇒，‎ ‎∴不存在λ，使a＝λb，‎ 即a与b不共线．‎ ‎[B级　能力提升]‎ 下列条件使M与A、B、C一定共面的是(　　)‎ A.＝2 －＋ B.＋＋＋＝0‎ C.＝＋＋ D.＋＋＝0‎ 解析：选D.根据共面向量定理知A、B、C均错，只有D能使其一定共面．‎ 如图所示空间四边形ABCD，连接AC、BD，设M、G分别是BC、CD的中点，则－＋等于(　　)‎ A. B．3 C．3 D．2 解析：选B.－＋＝－(－)＝－＝＋＝＋2 ＝3 .‎ 有下列命题：‎ ‎①若∥，则A，B，C，D四点共线；‎ ‎②若∥，则A，B，C三点共线；‎ ‎③若e1，e2为不共线的非零向量，a＝4e1－e2，b＝－e1＋e2，则a∥b；‎ ‎④若向量e1，e2，e3是三个不共面的向量，且满足等式k1e1＋k2e2＋k3e3＝0，则k1＝k2＝k3＝0.其中是真命题的序号是__________(把所有真命题的序号都填上)．‎ 解析：根据共线向量的定义，若∥，则AB∥CD或A，B，C，D四点共线，故①错；∥且，有公共点A，所以②正确；由于a＝4e1－e2＝－4＝－4b，所以a∥b.故③正确；易知④也正确．‎ 答案：②③④‎ 对于任意空间四边形ABCD，E、F分别是AB、CD的中点，试判断：与、的关系．‎ 解：如图所示，空间四边形ABCD中，E、F分别是AB、CD的中点，利用多边形加法法则可得，‎ ＝＋＋　①‎ ＝＋＋　②‎ 又＝－，＝－　③‎ 将③代入①得＝－＋－　④‎ ‎②＋④得2 ＝＋，‎ 所以＝＋，‎ 即与、共面．‎ (创新题)如图，正方体ABCD－A1B‎1C1D1中，M为DD1的中点，N在AC上，且AN∶NC＝2∶1，求证：与、共面．‎ 证明：＝－，＝＋＝－，‎ ＝＝(＋)，‎ ‎∴＝－＝(＋)－ ‎＝(－)＋(－)‎ ‎＝＋.‎ ‎∴与、共面． ‎