高中数学选修2-2教学课件1_3_2 函数的极值与导数

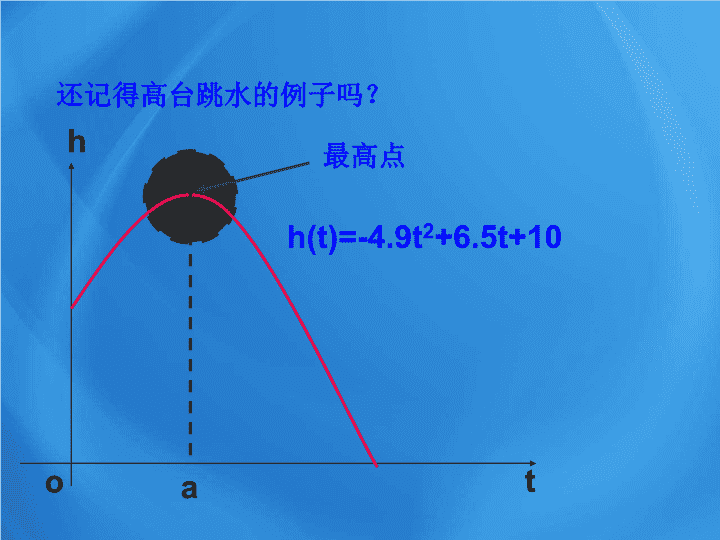
高中数学选修2-2教学课件1_3_2 函数的极值与导数

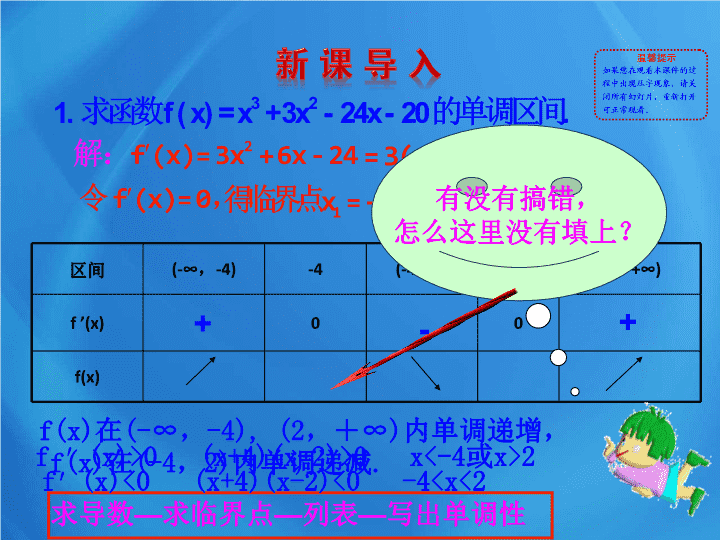
1.3.2 函数的极值与导数 区间 (-∞ ， -4) -4 (-4 ， 2) 2 (2 ， +∞) f ’(x) 0 0 f(x) f(x) 在 (-∞ ， -4), (2 ，＋∞ ) 内单调递增， 你记住了吗？ 有没有搞错， 怎么这里没有填上？ 求导数 — 求临界点 — 列表 — 写出单调性 + + - f ′ (x)>0 (x+4)(x-2)>0 x<-4 或 x>2 f(x) 在 (-4 ， 2) 内单调递减 . f ′ (x)<0 (x+4)(x-2)<0 -40 单调递减 h ´ (t)<0 h ´ (a) ＝ 0 2. 跳水运动员在最高处附近的情况： (1) 当 t=a 时运动员距水面高度最大， h(t) 在此点的导数是多少呢？ (2) 当 ta 时 h(t) 的单调性是怎样的呢？ 将最高点附近放大 t=a ta a t h o 最高点 导数的符号有什么变化规律？ 在 t=a 附近， h(t) 先增后减， h ′ (t) 先正后负， h ′ (t) 连续变化，于是有 h ′ (a)=0,f(a) 最大 . 那么下面图象的最高点 h （ a ）代表什么意义呢？ 这就是本节课研究的重点 —— 函数的极值 ＋ － h(t)=-4.9t 2 +6.5t+10 1. 探索并应用函数极值与导数的关系求函数 极值 . （重点） 2. 利用导数信息判断函数极值的情况 . （难点） 探究点 函数的极值与导数 求可导函数 f(x) 极值的步骤： (2) 求导数 f ′ (x) ； (3) 求方程 f ′ (x) =0 的根； (4) 把定义域划分为 部分区间，并列成表格 检查 f ′ (x) 在方程根左右的符号 —— 如果 左正右负 （ + ～ - ）， 那么 f(x) 在这个根处取得极 大 值； 如果 左负右正 （ - ～ + ）， 那么 f(x) 在这个根处取得极 小 值； (1) 确定函数的 定义域 ； 总结提升 1. 下面说法正确的是 . A. 可导函数必有极值 B. 可导函数在极值点的导数一定等于零 C. 函数的极小值一定小于极大值 （设极小值、极大值都存在） D. 函数的极小值（或极大值）不会多于一个 B 注意： 函数极值是在某一点附近的小区间内定义的，是局部性质 . 因此一个函数在其整个定义区间上可能 有多个极大值或极小值，并对同一个函数来说，在 某一点的极大值也可能小于另一点的极小值 . 2. 函数 y = f ( x ) 的导数 y ′ 与函数值和极值之间的关系 为 ( ) A. 导数 y ′ 由负变正 , 则函数 y 由减变为增 , 且有极大值 B. 导数 y ′ 由负变正 , 则函数 y 由增变为减 , 且有极大值 C. 导数 y ′ 由正变负 , 则函数 y 由增变为减 , 且有极小值 D. 导数 y ′ 由正变负 , 则函数 y 由增变为减 , 且有极大值 D 函数 在 时有极值 10 ，则 a ， b 的值为（ ） A. 或 B. 或 C. D. 以上都不对 C 3. 解 : 由题设条件得： 解之得 通过验证， a=3,b=3 时，不合题意 . 注意： f ′ (x 0 )=0 是函数取得极值的必要不充分条件 . 注意代入检验 . 解： (1) 由图象可知： (2) 注意数形结合 极值定义 2 个关键 ①可导函数 y=f(x) 在极值点处的 f ′ (x)=0 . ② 极值点左右两边的导数必须 异号 . 3 个步骤 ① 确定定义域 ② 求 f ′ (x)=0 的根 ③ 并列成表格 用方程 f ′ (x)=0 的根，顺次将函数的定义域 分成若干个开区间，并列成表格由 f ′ (x) 在方程 根左右的符号，来判断 f(x) 在这个根处取极值的情况 . 我以为挫折、磨难是锻炼意志、增强能力的好机会 . —— 邹韬奋