- 2021-06-23 发布 |
- 37.5 KB |
- 7页

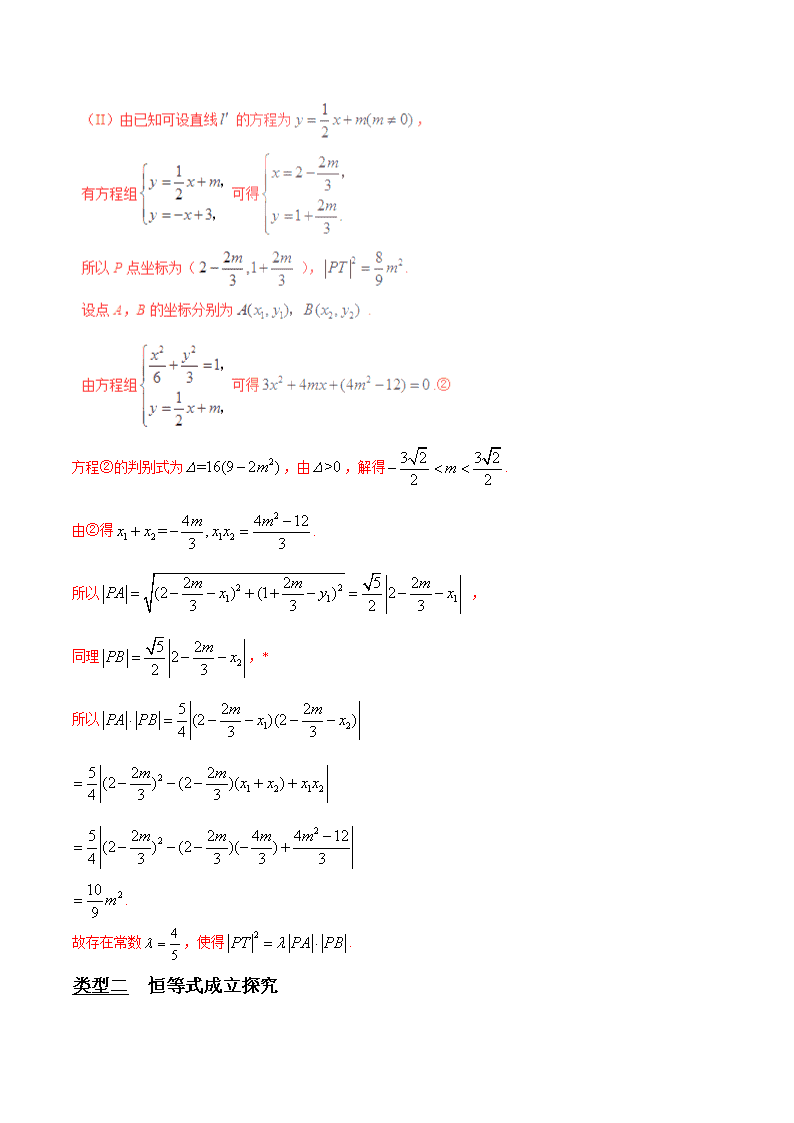

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届二轮复习探究代数表达式,函数方程来发力学案(全国通用)
【题型综述】 探究代数表达式包括以下若干类型:(1)参数值的探索,根据题中的条件将参数转化为关于直线与圆锥曲线的交点的坐标的方程或函数问题,若利用设而不求思想与韦达定理即可求出参数的值即存在,否则不存在 .(2)等式恒成立问题,根据题中条件和有关向量、距离公式、平面几何知识等方法,转化为关于直线与圆锥曲线的交点的坐标的方程或函数问题,若利用设而不求思想与韦达定理即可求出参数的值即存在。 【典例指引】 类型一 参数值的探究 例1 【2016年高考四川理数】(本小题满分13分) 已知椭圆E:的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线与椭圆E有且只有一个公共点T. (Ⅰ)求椭圆E的方程及点T的坐标; (Ⅱ)设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数,使得,并求的值. 方程②的判别式为,由,解得. 由②得. 所以 , 同理,* 所以 . 故存在常数,使得. 类型二 恒等式成立探究 例2. 【2015高考四川,理20】如图,椭圆E:的离心率是,过点P(0,1)的动直线与椭圆相交于A,B两点,当直线平行与轴时,直线被椭圆E截得的线段长为. (1)求椭圆E的方程; (2)在平面直角坐标系中,是否存在与点P不同的定点Q,使得恒成立?若存在,求出点Q的坐标;若不存在,请说明理由. (2)当直线与轴平行时,设直线与椭圆相交于C、D两点. 如果存在定点Q满足条件,则,即. 所以Q点在y轴上,可设Q点的坐标为. 当直线与轴垂直时,设直线与椭圆相交于M、N两点. 则, 由,有,解得或. 所以,若存在不同于点P的定点Q满足条件,则Q点的坐标只可能为. 下面证明:对任意的直线,均有.* 当直线的斜率不存在时,由上可知,结论成立. 当直线的斜率存在时,可设直线的方程为,A、B的坐标分别为. 联立得.* 其判别式,类型三 面积最小值存在性 例3【2015高考湖北,文22】一种画椭圆的工具如图1所示.是滑槽的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且,.当栓子D在滑槽AB内作往复运动时,带动N绕转动,M处的笔尖画出的椭圆记为C.以为原点,所在的直线为轴建立如图2所示的平面直角坐标系. (Ⅰ)求椭圆C的方程; (Ⅱ)设动直线与两定直线和分别交于两点.若直线总与椭圆有且只有一个公共点,试探究:的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由. x D O M N y 第22题图2 第22题图1 . ② 将①代入②得,. 当时,;当时,.因,则,,所以,当且仅当时取等号.所以当时,的最小值为8. * 综合(1)(2)可知,当直线与椭圆在四个顶点处相切时,的面积取得最小值8. 类型四 面积关系探究 例4.(2011湖南理21)如图7,椭圆的离心率为,轴被曲线截得的线段长等于的长半轴长. (Ⅰ)求的方程; (Ⅱ)设与轴的交点为,过坐标原点的直线与相交于点,直线分别与相交于点. (ⅰ)求证:; (ⅱ)记的面积分别为.问:是否存在直线,使得?请说明理由. 【扩展链接】 1. 为椭圆的其中一个焦点,若是椭圆上一点,则. 2. 为双曲线的右焦点,若是双曲线右支上一点,则,若是双曲线左支上一点,则,. 3. 为椭圆的左焦点,是过左焦点倾斜角为的弦,点在轴上方,则,,,. 4. 为抛物线的焦点,是过左焦点倾斜角为的弦,点在轴上方,则,,,.查看更多