高考数学专题复习:综合素能检测必修一
第一章综合素能检测 必修一
一、选择题
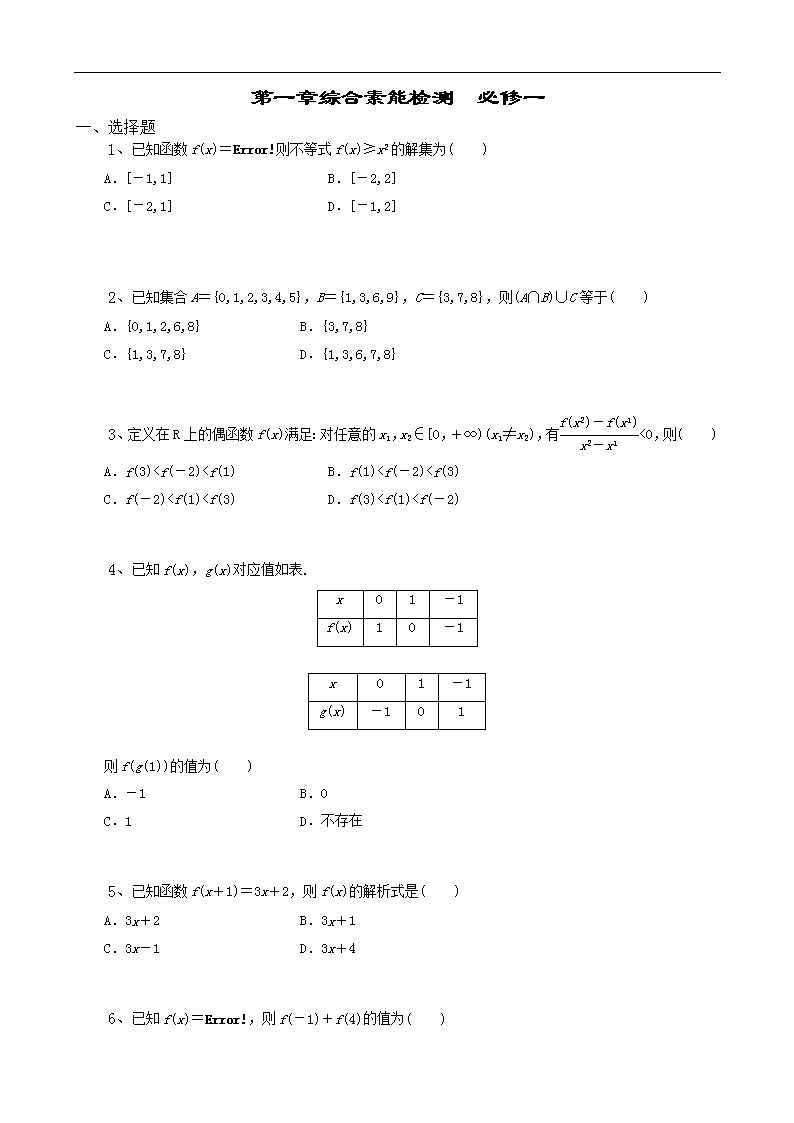
1、已知函数f(x)=则不等式f(x)≥x2的解集为( )
A.[-1,1] B.[-2,2]
C.[-2,1] D.[-1,2]
2、已知集合A={0,1,2,3,4,5},B={1,3,6,9},C={3,7,8},则(A∩B)∪C等于( )
A.{0,1,2,6,8} B.{3,7,8}
C.{1,3,7,8} D.{1,3,6,7,8}
3、定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有<0,则( )
A.f(3)
0).
18、(本题满分12分)设集合A={x|a≤x≤a+3},集合B={x|x<-1或x>5},分别就下列条件求实数a的取值范围:
(1)A∩B≠∅,(2)A∩B=A.
19、(本题满分12分)二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围.
20、(本题满分12分)图中给出了奇函数f(x)的局部图象,已知f(x)的定义域为[-5,5],试补全其图象,并比较f(1)与f(3)的大小.
21、(本题满分12分)一块形状为直角三角形的铁皮,直角边长分别为40cm与60cm现将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪法,才能使剩下的残料最少?
22、(本题满分12分)
(1)若a<0,讨论函数f(x)=x+,在其定义域上的单调性;
(2)若a>0,判断并证明f(x)=x+在(0,]上的单调性.
以下是答案
一、选择题
1、A[解析] 解法1:当x=2时,f(x)=0,f(x)≥x2不成立,排除B、D;当x=-2时,f(x)=0,也不满足f(x)≥x2,排除C,故选A.
解法2:不等式化为或,
解之得,-1≤x≤0或00,则f(x2)-f(x1)<0,
即f(x2)2>1,∴f(3)420,设稿费x元,x<4000,则(x-800)×14%=420,∴x=3800(元).
16、(0,2][解析] a<0时,f(x)在定义域上是增函数,不合题意,∴a>0.
由2-ax≥0得,x≤,∴f(x)在(-∞,]上是减函数,由条件≥1,∴0.
(2)F(x)=|x-a|-ax,∵0f(x2),∴f(x)在(0,]上单调减.
18、[解析] (1)因为A∩B≠∅,所以a<-1或a+3>5,即a<-1或a>2.
(2)因为A∩B=A,所以A⊆B,所以a>5或a+3<-1,即a>5或a<-4.
19、[解析] (1)∵f(x)为二次函数且f(0)=f(2),
∴对称轴为x=1.
又∵f(x)最小值为1,∴可设f(x)=a(x-1)2+1 (a>0)
∵f(0)=3,∴a=2,∴f(x)=2(x-1)2+1,
即f(x)=2x2-4x+3.
(2)由条件知2a<1f(1).
21、[解析] 如图,剪出的矩形为CDEF,设CD=x,CF=y,则AF=40-y.
∵△AFE∽△ACB.
∴=即∴=
∴y=40-x.剩下的残料面积为:
S=×60×40-x·y=x2-40x+1 200=(x-30)2+600
∵00,