2020届高三数学（文）“大题精练”5

2020届高三数学（文）“大题精练”5

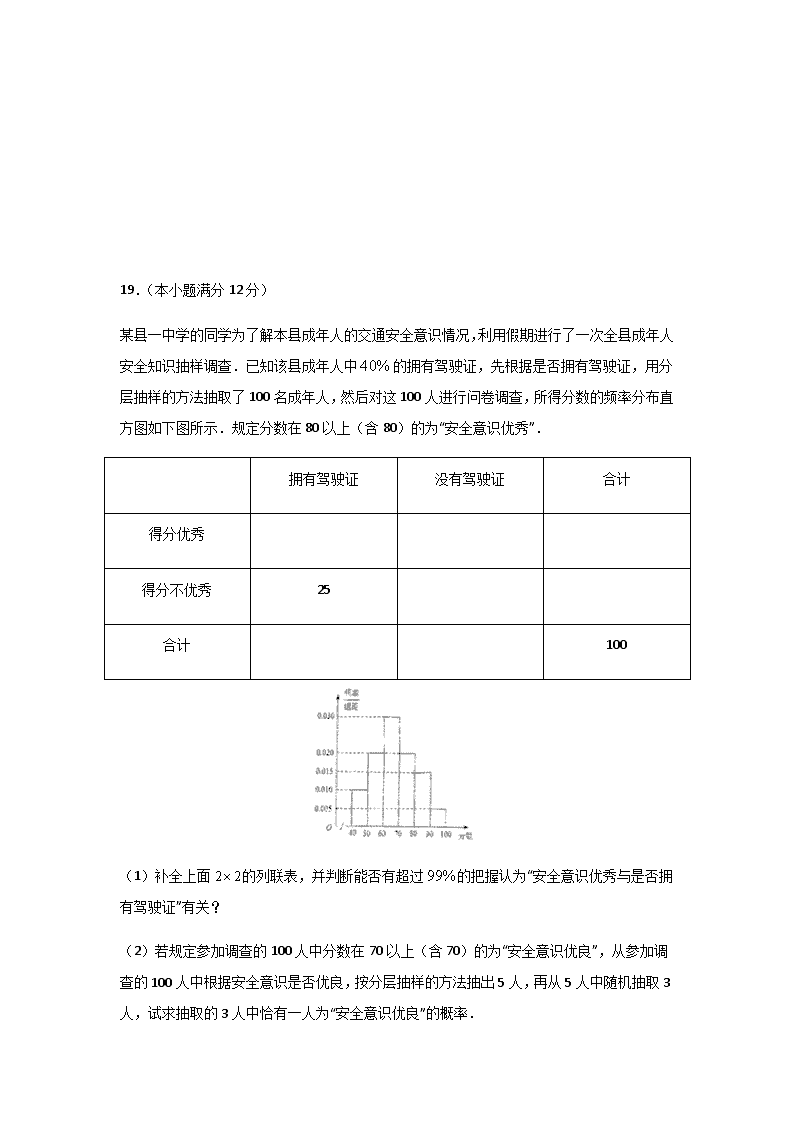
‎2020届高三数学（文）“大题精练”5‎ ‎17．（本小题满分12分）‎ 已知数列满足，，其中为的前项和，．‎ ‎（1）求；‎ ‎（2）若数列满足，求的值．‎ ‎18．（本小题满分12分）‎ 如图，在三棱柱中，是棱的中点．‎ ‎（1）证明：平面．‎ ‎（2）若是棱上的任意一点，且三棱柱的体积为，求三棱锥的体积．‎ ‎19．（本小题满分12分）‎ 某县一中学的同学为了解本县成年人的交通安全意识情况，利用假期进行了一次全县成年人安全知识抽样调查．已知该县成年人中的拥有驾驶证，先根据是否拥有驾驶证，用分层抽样的方法抽取了100名成年人，然后对这100人进行问卷调查，所得分数的频率分布直方图如下图所示．规定分数在80以上（含80）的为“安全意识优秀”．‎ 拥有驾驶证 没有驾驶证 合计 得分优秀 得分不优秀 ‎25‎ 合计 ‎100‎ ‎（1）补全上面的列联表，并判断能否有超过的把握认为“安全意识优秀与是否拥有驾驶证”有关？‎ ‎（2）若规定参加调查的100人中分数在70以上（含70）的为“安全意识优良”，从参加调查的100人中根据安全意识是否优良，按分层抽样的方法抽出5人，再从5人中随机抽取3人，试求抽取的3人中恰有一人为“安全意识优良”的概率．‎ 附表及公式：，其中．‎ ‎0．15‎ ‎0．10‎ ‎0．05‎ ‎0．025‎ ‎0．010‎ ‎0．005‎ ‎0．001‎ ‎2．072‎ ‎2．706‎ ‎3．841‎ ‎5．024‎ ‎6．635‎ ‎7．879‎ ‎10．828‎ ‎20．（本小题满分12分）‎ 已知椭圆：的左右顶点分别为，，点是椭圆上异于、的任意一点，设直线，的斜率分别为、，且，椭圆的焦距长为4．‎ ‎（1）求椭圆的离心率；‎ ‎（2）过右焦点且倾斜角为的直线交椭圆于、两点，分别记，的面积为、，求的值．‎ ‎21．（本小题满分12分）‎ 已知函数．‎ ‎（1）讨论的单调性．‎ ‎（2）试问是否存在，使得对恒成立？若存在，求的取值范围；若不存在，请说明理由．‎ 请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．选修4-4：坐标系与参数方程（本小题满分10分）‎ 已知曲线的极坐标方程是，以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程（为参数）．‎ ‎（1）写出直线的普通方程与曲线的直角坐标方程；‎ ‎（2）设曲线经过伸缩变换得到曲线，设曲线上任一点为，求点到直线距离的最大值．‎ ‎23．选修4-5：不等式选讲（本小题满分10分）‎ 已知关于x的不等式．‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若该不等式有实数解，求实数a的取值范围．‎ ‎2020届高三数学（文）“大题精练”5（答案解析）‎ ‎17．（本小题满分12分）‎ 已知数列满足，，其中为的前项和，．‎ ‎（1）求；‎ ‎（2）若数列满足，求的值．‎ ‎【解析】（1），，，两式相减得，‎ 注意到，，于是，所以．‎ ‎（2），于是，‎ 所以．‎ ‎18．（本小题满分12分）‎ 如图，在三棱柱中，是棱的中点．‎ ‎（1）证明：平面．‎ ‎（2）若是棱上的任意一点，且三棱柱的体积为，求三棱锥的体积．‎ ‎【解析】（1）连接交于点，连接．‎ 因为四边形是平行四边形，所以是的中点．‎ 因为是的中点，所以．‎ 又平面，平面，所以平面．‎ ‎（2）设三棱柱的高为，底面的面积为，‎ 则三棱柱的体积．‎ 又，，所以．‎ ‎19．（本小题满分12分）‎ 某县一中学的同学为了解本县成年人的交通安全意识情况，利用假期进行了一次全县成年人安全知识抽样调查．已知该县成年人中的拥有驾驶证，先根据是否拥有驾驶证，用分层抽样的方法抽取了100名成年人，然后对这100人进行问卷调查，所得分数的频率分布直方图如下图所示．规定分数在80以上（含80）的为“安全意识优秀”．‎ 拥有驾驶证 没有驾驶证 合计 得分优秀 得分不优秀 ‎25‎ 合计 ‎100‎ ‎（1）补全上面的列联表，并判断能否有超过的把握认为“安全意识优秀与是否拥有驾驶证”有关？‎ ‎（2）若规定参加调查的100人中分数在70以上（含70）的为“安全意识优良”，从参加调查的100人中根据安全意识是否优良，按分层抽样的方法抽出5人，再从5人中随机抽取3人，试求抽取的3人中恰有一人为“安全意识优良”的概率．‎ 附表及公式：，其中．‎ ‎0．15‎ ‎0．10‎ ‎0．05‎ ‎0．025‎ ‎0．010‎ ‎0．005‎ ‎0．001‎ ‎2．072‎ ‎2．706‎ ‎3．841‎ ‎5．024‎ ‎6．635‎ ‎7．879‎ ‎10．828‎ ‎【解析】（1）由题意可知拥有驾驶证的人数为：人，则拥有驾驶证且得分为优秀的人数为：人，由频率分布直方图知得分优秀的人数为：人，没有驾驶证且得分优秀的人数为：人，则没有驾驶证且得分不优秀的人数为：人，可得列联表如下：‎ 拥有驾驶证 没有驾驶证 合计 得分优秀 得分不优秀 合计 ‎，‎ 有超过的把握认为“安全意识优秀与是否拥有驾驶证”有关．‎ ‎（2）由频率分布直方图可求得以上（含）的人数为：，‎ 按分层抽样的方法抽出人时，“安全意识优良”的有人，记为；‎ 其余的人记为，从中随机抽取人，基本事件有：，，，，，，，，，共个，恰有一人为“安全意识优良”的事件有个，恰有一人为“安全意识优良”的概率为：，‎ ‎20．（本小题满分12分）‎ 已知椭圆：的左右顶点分别为，，点是椭圆上异于、的任意一点，设直线，的斜率分别为、，且，椭圆的焦距长为4．‎ ‎（1）求椭圆的离心率；‎ ‎（2）过右焦点且倾斜角为的直线交椭圆于、两点，分别记，‎ 的面积为、，求的值．‎ ‎【解析】（1）设点，则，①‎ ‎∵，②‎ ‎∴联立①②得，∴，∴，∴．‎ ‎（2）由题意知，，即，‎ 由（1）知，，∴，∴，，∴椭圆的方程为：．‎ 由已知得：，联立，可得．‎ 设，，根据韦达定理，得，‎ 于是．‎ ‎21．（本小题满分12分）‎ 已知函数．‎ ‎（1）讨论的单调性．‎ ‎（2）试问是否存在，使得对恒成立？若存在，求的取值范围；若不存在，请说明理由．‎ ‎【解析】（1），．‎ 当时，，在上单调递增；‎ 当时，，在上单调递减，在上单调递增；‎ 当时，在上单调递减，在，上单调递增； ‎ 当时，在上单调递减，在，上单调递增．‎ ‎（2）假设存在，使得对恒成立．‎ 则，即，‎ 设，则存在，使得，‎ 因为，所以在上单调递增，‎ 因为，所以时即．‎ 又因为对恒成立时，需，‎ 所以由（1）得：‎ 当时，在上单调递增，所以，‎ 且成立，从而满足题意；‎ 当时，在上单调递减，在，上单调递增，‎ 所以所以（*）．‎ 设，，则在上单调递增，‎ 因为，所以的零点小于2，从而不等式组（*）的解集为，所以即．‎ 综上，存在，使得对恒成立，且的取值范围为．‎ 请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．选修4-4：坐标系与参数方程（本小题满分10分）‎ 已知曲线的极坐标方程是，以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程（为参数）．‎ ‎（1）写出直线的普通方程与曲线的直角坐标方程；‎ ‎（2）设曲线经过伸缩变换得到曲线，设曲线上任一点为，求点到直线距离的最大值．‎ ‎【解析】（1）直线的普通方程：，曲线的直角坐标方程：．‎ ‎（2）曲线：，设，，其中为辅助角，当时，取最大值为．‎ ‎23．选修4-5：不等式选讲（本小题满分10分）‎ 已知关于x的不等式．‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若该不等式有实数解，求实数a的取值范围．‎ ‎【解析】（1）当时，令，‎ 当时，，解得；‎ 当时，，不等式恒成立；‎ 当时，，解得．‎ 综上所述，不等式的解集为．‎ ‎（2），所以，‎ 即，解得