数学理卷·2018届陕西省普通高等学校高三招生全国统一考试模拟试题（四）（2018

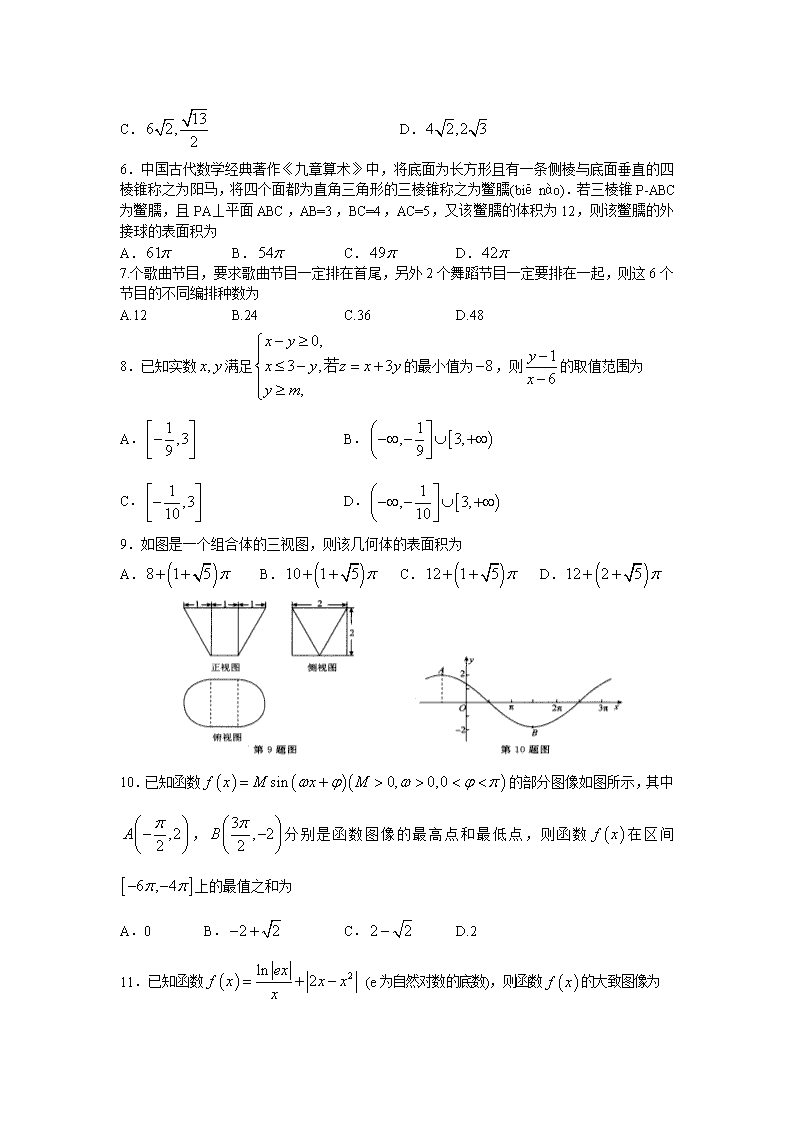
数学理卷·2018届陕西省普通高等学校高三招生全国统一考试模拟试题（四）（2018

‎2018届陕西省普通高等学校高三招生全国统一考试模拟试题 理科数学(四)‎ 本试卷满分150分，考试时间120分钟．‎ 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名、准考证号填写在答题纸上．‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题纸上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题纸上，写在本试卷上无效．‎ ‎3．考试结束后，将本试卷和答题纸一并交回．‎ 一、选择题：本题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知全集U=R，集合，‎ 则 A．[2，10) B．(2，10) C．(0，2) D．‎ ‎2．已知i为虚数单位，若复数为纯虚数，则的共轭复数在复平面内所对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．某品牌家电厂商为了扩大知名度，在一段时期内进行广告宣传．已知其广告费用x(单位：万元)与销售额y(单位：万元)具有线性关系，其前五个月的统计数据如下表：‎ 由上表可得线性回归方程，据此模型预估广告费用为8万元时的销售额是 A．108万元 B．115万元 ‎ C．118万元 D．123万元 ‎4．执行如图所示的程序框图，则输出S的值为 A．2 B．‎ C． D．‎ ‎5．与双曲线有共同的渐近线，且经过点的双曲线的虚轴长和离心率分别为 A． B．‎ C． D．‎ ‎6．中国古代数学经典著作《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑(biē nào)．若三棱锥P-ABC为鳖臑，且PA⊥平面ABC，AB=3，BC=4，AC=5，又该鳖臑的体积为12，则该鳖臑的外接球的表面积为 A． B． C． D．‎ ‎7.个歌曲节目，要求歌曲节目一定排在首尾，另外2个舞蹈节目一定要排在一起，则这6个节目的不同编排种数为 A.12 B.24 C.36 D.48‎ ‎8．已知实数满足的最小值为，则的取值范围为 A． B．‎ C． D．‎ ‎9．如图是一个组合体的三视图，则该几何体的表面积为 A． B． C． D．‎ ‎10．已知函数的部分图像如图所示，其中，分别是函数图像的最高点和最低点，则函数在区间上的最值之和为 A．0 B． C． D.2‎ ‎11．已知函数 (e为自然对数的底数)，则函数的大致图像为 ‎12．已知椭圆的离心率为e，点R(2，1)在椭圆内部，过点R作两条直线与椭圆C分别交于点M，P和点N，Q，且，则椭圆C的离心率为 A． B． C． D．‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13．已知的展开式中的常数项为4860，则展开式中所有项的系数之和为___________．‎ ‎14．把数列的各项依次排列，如图所示，则第11行的第15个数为_________．‎ ‎15．已知点为坐标原点，且上的投影为，则向量的夹角的余弦值为___________．‎ ‎16．已知在△ABC中，角A，B，C所对的边分别为 ‎，的面积为的周长为___________．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．‎ ‎(一)必考题：共60分．‎ ‎17．(12分)‎ 已知数列的前n项和满足 ‎.‎ ‎(1)求数列和的通项公式，‎ ‎(2)若，求数列的前n项和．‎ ‎18．(12分)‎ 近年来随着共享经济的发展以及商机的不断涌现，共享理念得到了广泛的普及，共享单车、共享篮球、共享充电宝等层出不穷．伴随着共享经济的不断扩大，国内企业纷纷跳入共享的大海，希望能够分一杯羹．某公司为了能够扩大经营，增加公司的年利润，复制其他公司成功的共享模式，特派遣该公司部分男女职工到国外对共享经济进行研究与学习，该公司为了解不同性别的职工对被外派工作的意愿，按分层抽样的方式从男职工和女职工中随机抽取200名职工进行调查，得到数据如下表：‎ ‎(1)在参加调查的200名职工中随机抽取1名，求抽到愿意被外派的职工的概率．‎ ‎(2)外派之前，公司考虑对3名职工进行额外的培训，且参加完培训后每名职工都必须参加结业考试．每个培训后的职工通过考试的概率为，若通过考试，则职工结业，否则进行补考，补考通过的概率为，若补考未通过，则职工此次培训不能结业．记每人参加培训的费用为1 000元，首次考试的费用为100元，补考的费用为200元，假设每名职工是否通过考试相互独立，记X为任意2名职工参加培训的总费用(总费用包括培训费用、首次考试费用以及补考费用)，若E(X)>2500元，则成本太高，不安排培训；若E(X)≤2500元，则可以安排培训．请通过计算说明是否对被派遣的3名职工进行额外的培训．‎ ‎19．(12分)‎ 已知四边形ABCD为等腰梯形，分别过点平面ABCD，连接相关线段，所得图形如图所示，其中AD=AB=BC=AE=CF=1，∠BAD=120°，G是线段EF上的点．‎ ‎(1)若点M在线段CD上，且CM=1，证明：平面ACFE．‎ ‎(2)试确定点G的位置，使得平面CGD与平面BEF所成角的余弦值为．‎ ‎【来源：全,品…中&高*考+网】‎ ‎20．(12分)‎ 已知在平面直角坐标系中，点P(1，0)，点Q在直线上，点M满足，记点M的轨迹为曲线E．‎ ‎(1)求曲线E的方程；‎ ‎(2)若直线与曲线E在x轴上方的部分交于A，D两点(A在D的左侧)，轴，垂足为轴，垂足为C，记的取值范围．‎ ‎21．(12分)‎ 已知函数．‎ ‎(1)若，求函数的极值；‎ ‎(2)若关于的不等式内恒成立，求实数m的取值范围.【来源：全,品…中&高*考+网】‎ ‎(二)选考题：共10分．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．[选修4-4：坐标系与参数方程](10分)‎ 在平面直角坐标系中，曲线的参数方程为(m为参数)，以坐标原点O为极点，轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎(1)求曲线的普通方程以及曲线的参数方程；【来源：全,品…中&高*考+网】‎ ‎(2)已知点，曲线，交于M，N两点，求的值．【来源：全,品…中&高*考+网】‎ ‎23．[选修4-5：不等式选讲](10分)‎ 已知函数．【来源：全,品…中&高*考+网】‎ ‎(1)若关于的不等式有解，求实数a的取值范围；‎ ‎(2)若关于的不等式的解集为，且正实数m，n满足的最小值．‎