2019高三数学(人教B版理)一轮:单元质检卷二+函数
单元质检卷二 函数
(时间:100分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知集合A={x|y=lg(2x+1)},B={x||x|<3},则A∩B=( )
A.-12,0 B.(0,3)
C.-12,3 D.-3,-12
2.(2017河南郑州、平顶山、濮阳二模,理2)若x=30.5,y=log32,z=cos 2,则( )
A.z
0,b>0,则“a>b”是“a+ln a>b+ln b”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.已知函数f(x)的定义域为R.当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>12时,fx+12=fx-12,则f(6)=( )
A.-2 B.-1
C.0 D.2
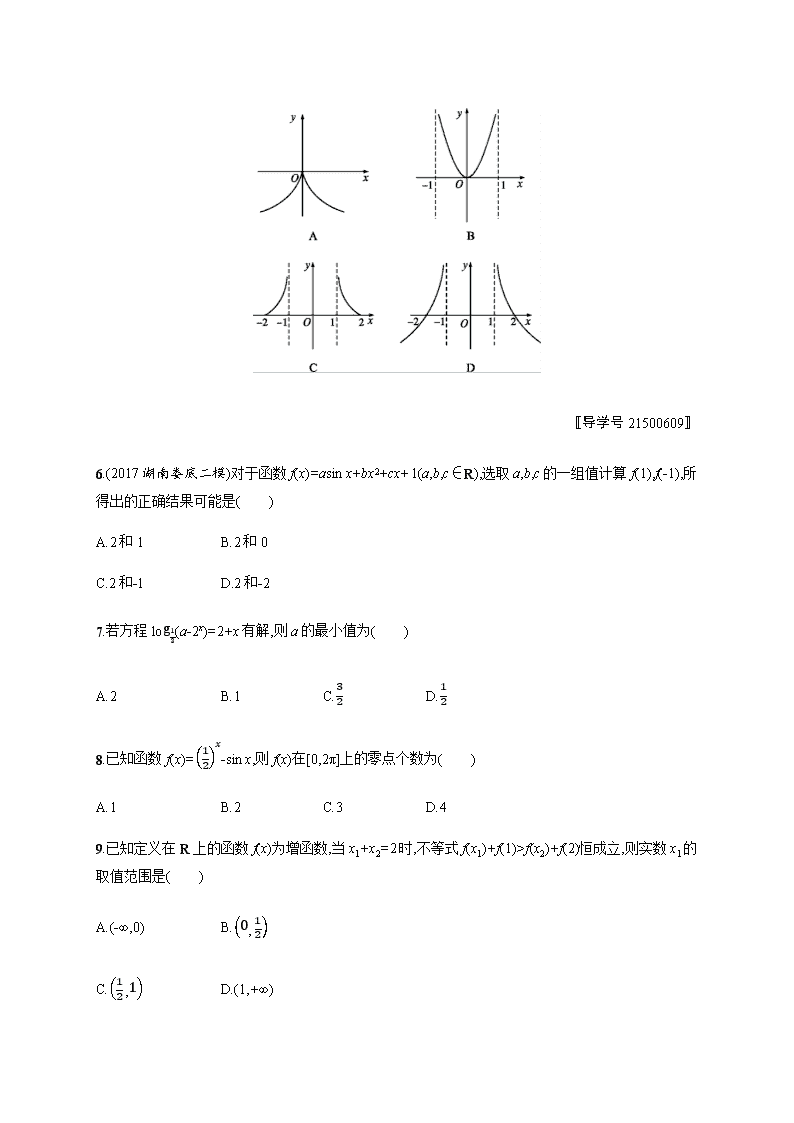
5.已知函数f(x)=logax(0f(x2)+f(2)恒成立,则实数x1的取值范围是( )
A.(-∞,0) B.0,12
C.12,1 D.(1,+∞)
10.(2017河南豫南九校考评,理11)若函数f(x)=|logax|-2-x(a>0,a≠1)的两个零点是m,n,则( )
A.mn=1 B.mn>1
C.mn<1 D.以上都不对
11.某公司租地建仓库,已知仓库每月占用费y1与仓库到车站的距离成反比,而每月车载货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
A.5千米处 B.4千米处
C.3千米处 D.2千米处
12.已知函数f(x)=|x|+2,x<1,x+2x,x≥1.设a∈R,若关于x的不等式f(x)≥x2+a在R上恒成立,则a的取值范围是( )
A.[-2,2] B.[-23,2]
C.[-2,23] D.[-23,23]〚导学号21500610〛
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知p:函数f(x)=|x+a|在(-∞,-1)内是单调函数,q:函数g(x)=loga(x+1)(a>0,且a≠1)在(-1,+∞)内是增函数,则¬p成立是q成立的 .(填“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)
14.已知函数f(x)=1+cosπx2,x>1,x2,00),若存在唯一的x0,使得h(x)=min{f(x),g(x)}的最小值为h(x0),则实数a的取值范围为 .
15.(2017江西五调,理15)已知函数f(x)(x∈R)满足f(-x)=4-f(x),函数g(x)=x-2x-1+xx+1,若曲线y=f(x)与y=g(x)的交点分别为(x1,y1),(x2,y2),…,(xm,ym),则∑i=1m(xi+yi)= .(结果用含有m的式子表示)〚导学号21500611〛
16.已知函数f(x)=9x-a3x的图象关于原点对称,g(x)=lg(10x+1)+bx是偶函数,则a+b= .
三、解答题(本大题共5小题,共70分)
17.(14分)已知函数f(x)=m+logax(a>0,且a≠1)的图象过点(8,2)和(1,-1).
(1)求函数f(x)的解析式;
(2)令g(x)=2f(x)-f(x-1),求g(x)的最小值及取得最小值时x的值.
18.(14分)已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)=g(x)x.
(1)求a,b的值;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]上有解,求实数k的取值范围.
19.(14分)某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=13x2+10x;当年产量不少于80千件时,C(x)=51x+10 000x-1 450.通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(单位:万元)关于年产量x(单位:千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
〚导学号21500612〛
20.(14分)已知二次函数y=f(x)在x=t+22处取得最小值-t24(t≠0),且f(1)=0.
(1)求y=f(x)的表达式;
(2)若函数y=f(x)在区间-1,12上的最小值为-5,求此时t的值.
21.(14分)已知函数f(x)=lgx+ax-2,其中x>0,a>0.
(1)求函数f(x)的定义域;
(2)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围.
〚导学号21500613〛
参考答案
单元质检卷二 函数
1.C 由2x+1>0,得x>-12,∴A=-12,+∞,B={x||x|<3}=(-3,3).∴A∩B=-12,3.故选C.
2.A ∵x=30.5=3>1,0=log31b,∴f(a)>f(b),∴a+ln a>b+ln b,故充分性成立,
∵a+ln a>b+ln b,∴f(a)>f(b),
∴a>b,故必要性成立,
故“a>b”是“a+ln a>b+ln b”的充要条件,故选C.
4.D 由题意可知,当-1≤x≤1时,f(x)为奇函数;
当x>12时,由fx+12=fx-12可得f(x+1)=f(x).
所以f(6)=f(5×1+1)=f(1).
而f(1)=-f(-1)=-[(-1)3-1]=2.
所以f(6)=2.故选D.
5.A 由题意知,当x=0时,y=f(1)=0,排除C,D.当x=1时,y=f(2)<0,排除B,故选A.
6.B g(x)=asin x+bx2+cx为定义域上的奇函数,所以g(1)+g(-1)=0,所以f(1)+f(-1)=g(1)+g(-1)+2=2,故选B.
7.B 若方程log12(a-2x)=2+x有解,则122+x=a-2x有解,即1412x+2x=a有解.
∵1412x+2x≥1,当且仅当1412x=2x,
即x=-1时,等号成立,故a的最小值为1,故选B.
8.B 函数f(x)=12x-sin x在[0,2π]上的零点个数为函数y=12x的图象与函数y=sin x的图象在[0,2π]上的交点个数.在同一坐标系内画出两个函数的部分图象如图所示,由图象可知,两个函数的图象在区间[0,2π]上有两个不同的交点,故选B.
9.D 由题意,得f(x1)-f(x2)>f(2)-f(1),∵x1+x2=2,则有f(x1)-f(2-x1)>f(2)-f(1),
又函数f(x)为增函数,∴f(x1)+f(1)>f(x2)+f(2)恒成立转化为x1>2,2-x1<1,
解得x1>1,即实数x1的取值范围是(1,+∞).
10.C 由f(x)=0,得|logax|=2-x,函数y=|logax|,y=2-x=12x的图象如图所示.
由图象可知,n>1,01,则有-logam=12m,logan=12n,两式两边分别相减得loga(mn)=12n-12m<0,
∴00.当x=10时,两项费用y1,y2分别是2万元和8万元,可得k1=20,k2=45,故y1+y2=20x+45x≥220x·45x=8,当且仅当20x=45x,即x=5时取等号,故选A.
12.A 由f(x)=|x|+2,x<1,x+2x,x≥1得f(x)>0在R上恒成立,
∵关于x的不等式f(x)≥x2+a在R上恒成立,
∴关于x的不等式-f(x)≤x2+a≤f(x)在R上恒成立,
即关于x的不等式-x2-f(x)≤a≤f(x)-x2在R上恒成立.
令p(x)=-x2-f(x),
则p(x)=x2-2,x<0,-32x-2,0≤x<1,-32x-2x,x≥1.
当x<0时,p(x)<-2,
当0≤x<1时,-722,当0≤x<1时,2≤t(x)<52,当x≥1时,t(x)≥2,当且仅当x=2时取等号.
综上所述,t(x)min=2.
∵关于x的不等式-x2-f(x)≤a≤f(x)-x2在R上恒成立,
∴-2≤a≤2.故选A.
13.充要条件 由p成立,得a≤1;由q成立,得a>1.故¬p成立时a>1,即¬p是q成立的充要条件.
14.(-∞,-2) 作出函数f(x)=1+cosπx2,x>1,x2,01).
因为x2x-1=(x-1)2+2(x-1)+1x-1
=(x-1)+1x-1+2≥2(x-1)·1x-1+2=4,
当且仅当x-1=1x-1,即x=2时,等号成立,而函数y=log2x在(0,+∞)内单调递增,所以log2x2x-1-1≥log24-1=1,故当x=2时,函数g(x)取得最小值1.
18.解 (1)g(x)=a(x-1)2+1+b-a,因为a>0,所以g(x)在区间[2,3]上是增函数,
故g(2)=1,g(3)=4,解得a=1,b=0.
(2)由已知可得f(x)=x+1x-2,所以f(2x)-k·2x≥0可化为2x+12x-2≥k·2x,
化为1+12x2-2·12x≥k,令t=12x,则k≤t2-2t+1,
因为x∈[-1,1],故t∈12,2,记h(t)=t2-2t+1,因为t∈12,2,故h(t)max=1.故k≤1.
19.解 (1)当0950.
综上所述,当x=100时,L(x)取得最大值1 000,
即年产量为100千件时,该厂在这一商品的生产中所获利润最大.
20.解 (1)设f(x)=ax-t+222-t24(a>0).
因为f(1)=0,所以t24(a-1)=0.
又因为t≠0,所以a=1,
所以f(x)=x-t+222-t24(t≠0).
(2)因为f(x)=x-t+222-t24(t≠0),
所以当t+22<-1,即t<-4时,
f(x)在-1,12上的最小值f(x)min=f(-1)=-1-t+222-t24=-5,所以t=-92;
当-1≤t+22≤12,即-4≤t≤-1时,f(x)在-1,12上的最小值f(x)min=ft+22=-t24=-5,所以t=±25(舍去);
当t+22>12,即t>-1时,f(x)在-1,12上的最小值f(x)min=f12=12-t+222-t24=-5,
所以t=-212(舍去).
综上所述,t=-92.
21.解 (1)由x+ax-2>0,得x2-2x+ax>0.
因为x>0,所以x2-2x+a>0.
当a>1时,x2-2x+a>0恒成立,函数f(x)的定义域为(0,+∞);
当a=1时,函数f(x)的定义域为{x|x>0,且x≠1};
当01+1-a}.
(2)对任意x∈[2,+∞)恒有f(x)>0,
即x+ax-2>1对x∈[2,+∞)恒成立,
故a>3x-x2对x∈[2,+∞)恒成立.
令h(x)=3x-x2,
h(x)=3x-x2=-x-322+94在[2,+∞)内是减函数,于是h(x)max=h(2)=2.
故a>2,即a的取值范围是{a|a>2}.