2016届高考数学（理）5年高考真题备考试题库：第7章 第2节 空间几何体的表面积与体积

2016届高考数学（理）5年高考真题备考试题库：第7章 第2节 空间几何体的表面积与体积

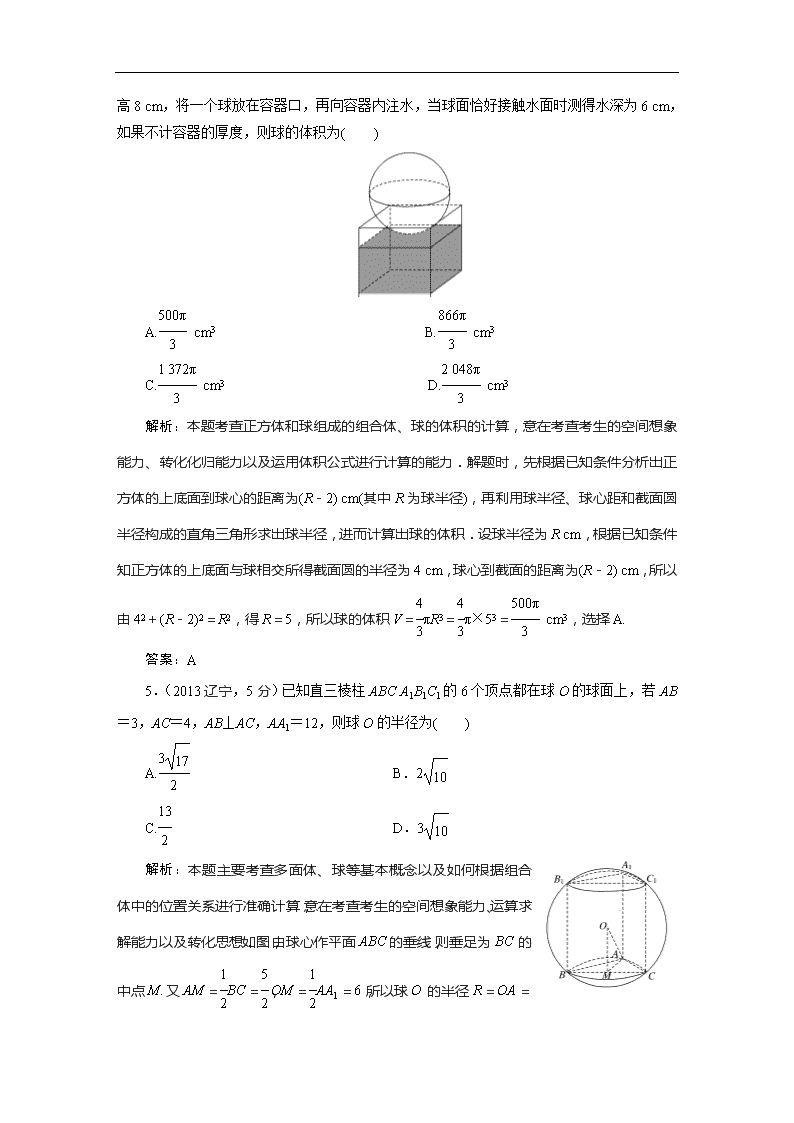
‎2010~2014年高考真题备选题库 第7章 立体几何 第2节 空间几何体的表面积与体积 ‎1．（2014陕西，5分）已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一个球面上，则该球的体积为(　　)‎ A. B．4π C．2π D. 解析：因为该正四棱柱的外接球的半径是四棱柱体对角线的一半，所以半径r＝＝1，所以V球＝×13＝.故选D.‎ 答案：D ‎2．（2014山东，5分）三棱锥P－ABC中，D，E分别为PB，PC的中点，记三棱锥D－ABE的体积为V1，P－ABC的体积为V2，则＝________.‎ 解析：如图，设点C到平面PAB的距离为h，三角形PAB的面积为S，则V2＝Sh，V1＝VE－ADB＝×S×h＝Sh，所以＝.‎ ‎3．（2014江苏，5分）设甲、乙两个圆柱的底面积分别为S1，S2，体积分别为V1，V2，若它们的侧面积相等，且＝，则的值是________．‎ 解析：设甲、乙两个圆柱的底面半径分别是r1，r2，母线长分别是l1，l2.则由＝可得＝.又两个圆柱的侧面积相等，即2πr‎1l1＝2πr‎2l2，则＝＝，所以＝＝×＝.‎ 答案： ‎4．（2013新课标全国Ⅰ，5分）如图，有一个水平放置的透明无盖的正方体容器，容器高‎8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为‎6 cm，如果不计容器的厚度，则球的体积为(　　)‎ A. cm3　　　　　　　　　　 B. cm3 ‎ C. cm3 D. cm3‎ 解析：本题考查正方体和球组成的组合体、球的体积的计算，意在考查考生的空间想象能力、转化化归能力以及运用体积公式进行计算的能力．解题时，先根据已知条件分析出正方体的上底面到球心的距离为(R－2) cm(其中R为球半径)，再利用球半径、球心距和截面圆半径构成的直角三角形求出球半径，进而计算出球的体积．设球半径为R cm，根据已知条件知正方体的上底面与球相交所得截面圆的半径为‎4 cm，球心到截面的距离为(R－2) cm，所以由42＋(R－2)2＝R2，得R＝5，所以球的体积V＝πR3＝π×53＝ cm3，选择A.‎ 答案：A ‎5．（2013辽宁，5分）已知直三棱柱ABCA1B‎1C1的6个顶点都在球O的球面上，若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为(　　)‎ A. B．2 C. D．3 解析：本题主要考查多面体、球等基本概念以及如何根据组合体中的位置关系进行准确计算，意在考查考生的空间想象能力、运算求解能力以及转化思想．如图，由球心作平面ABC的垂线，则垂足为BC的中点M.又AM＝BC＝，OM＝AA1＝6，所以球O的半径R＝OA＝ ＝.‎ 答案：C ‎6．（2012新课标全国，5分）已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为(　　)‎ A.　　　　　　　　　　 B. C. D. 解析：在直角三角形ASC中，AC＝1，∠SAC＝90°，SC＝2，所以SA＝＝；同理SB＝.过A点作SC的垂线交SC于D点，连接DB，因△SAC≌△SBC，故BD⊥SC，故SC⊥平面ABD，且平面ABD为等腰三角形，因∠ASC＝30°，故AD＝SA＝，则△ABD的面积为×1× ＝，则三棱锥的体积为××2＝.‎ 答案：A ‎7.（2012江西，5分）如右图，已知正四棱锥S－ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE＝x(0

查看更多