高中数学选修2-2课件1_1_3

高中数学选修2-2课件1_1_3

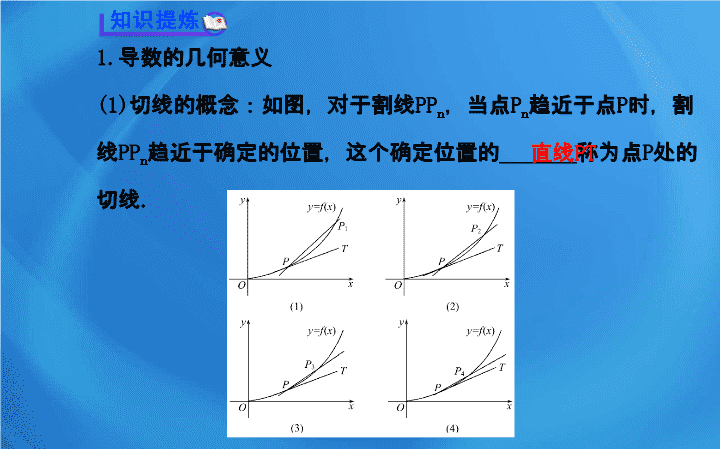
1.1.3 导数的几何意义 问题 引航 1. 导数的几何意义是什么 ? 2. 导函数的概念是什么 ? 怎样求导函数 ? 3. 怎么求过一点的曲线的切线方程 ? 1. 导数的几何意义 (1) 切线的概念：如图，对于割线 PP n ，当点 P n 趋近于点 P 时，割线 PP n 趋近于确定的位置，这个确定位置的 _______ 称为点 P 处的切线 . 直线 PT (2) 导数的几何意义：函数 f(x) 在 x=x 0 处的导数就是切线 PT 的斜率 k ，即 k= _______________=f′(x 0 ). 2. 导函数的概念 (1) 定义：当 x 变化时， _______ 便是 x 的一个函数，我们称它为 f(x) 的导函数 ( 简称导数 ). (2) 记法： f′(x) 或 y′ ，即 f′(x)=y′= _____________. f′(x) 1. 判一判 ( 正确的打 “ √ ” ，错误的打 “ × ” ) (1) 导函数 f′(x) 的定义域与函数 f(x) 的定义域相同 .( 　　 ) (2) 直线与曲线相切则直线与已知曲线只有一个公共点 .( 　　 ) (3) 函数 f(x)=0 没有导函数 .( 　　 ) 【 解析 】 (1) 错误 . 导函数 f′(x) 与原来的函数 f(x) 不一定有相同的定义域，如 y=lnx 的导数为 y′= (2) 错误 . 这条切线可能与已知曲线还有其他交点或切点 . (3) 错误 . 函数 f(x)=0 上每一点的导数都是 0 ，故函数 f(x)=0 的导函数是 f′(x)=0. 答案： (1)× 　　 (2)× 　　 (3)× 2. 做一做 ( 请把正确的答案写在横线上 ) (1) 已知函数 f(x) 在 x 0 处的导数为 f′(x 0 )=1 ，则函数 f(x) 在 x 0 处切线的倾斜角为 ________. (2) 若函数 f(x) 在点 A(1 ， 2) 处的导数是 -1 ，那么过点 A 的切线方程是 ________. (3) 函数 f(x)=x 2 的导数 f′(x)=________. 【 解析 】 (1) 由题意知，函数 f(x) 在 x 0 处的导数 f′(x 0 ) 就是函数 f(x) 在 x 0 处切线的斜率 k ，由 k=1 得，倾斜角为 45°. 答案： 45° (2) 因为函数 f(x) 在点 A(1 ， 2) 处的导数是 -1 ，所以过点 A 的切线方程为 y-2=-(x-1) ，即 x+y-3=0. 答案： x+y-3=0 (3) 可利用导数定义求 f(x)=x 2 在 x=x 0 处的导数，再把 x 0 换成 x 即可 . 答案： 2x 【 要点探究 】 知识点 1 导数的几何意义 1. 对切线的三点说明 (1) 与该点的位置有关 . (2) 曲线的切线是由割线绕一点转动，当另一点无限接近这一点时割线趋于的直线 . (3) 曲线的切线并不一定与曲线只有一个交点，可以有多个，甚至可以无穷多 . 与曲线只有一个公共点的直线也不一定是曲线的切线 . 2. 曲线上某点处的导数与切线的关系 (1) 函数 f(x) 在 x 0 处有导数，则在该点处函数 f(x) 表示的曲线必有切线，且导数值是该切线的斜率 . (2) 函数 f(x) 表示的曲线在点 (x 0 ， f(x 0 )) 处有切线，但函数 f(x) 在该点处不一定可导，如 f(x)= 在 x=0 处有切线，但不可导 . 【 知识拓展 】 导数中的极限思想 (1) 极限的理解：当一个变量逐次所取的值无限趋于一个定值，最终使变量的值和该定值之差要多小就多小，这个定值就叫做所有其他值的极限值，特别地，当一个变量的数值 ( 绝对值 ) 无限地减小使之收敛到极限 0 ，就说这个变量无穷小 . (2) 连续的理解：函数在某点连续的定义，是当自变量的增量趋于零时，函数值的增量趋于零 . (3) 导数的理解：函数在某点处导数的定义，是当自变量的增量趋于零时，函数值的增量与自变量的增量之比的极限 . 【 微思考 】 (1) 割线 PP n 的斜率 k n 与切线 PT 的斜率 k 有什么关系 ? 提示： 割线 PP n 的斜率是 k n = ，当点 P n 沿着曲线无限接近点 P 时， k n 无限趋近于切线 PT 的斜率 k. (2) 曲线 “ 在点 P 处的切线 ” 与 “ 过点 P 的切线 ” 的差异是什么 ? 提示： 在点 P 处的切线，点 P 必为切点，过点 P 的切线，点 P 不一定是切点，点 P 也不一定在曲线上 . 【 即时练 】 1. 如图所示，函数 y=f(x) 的图象在点 P 处的切线方程是 y=-x+ 8 ，则 f(5) 和 f′(5) 分别为 ( 　　 ) A.3 ， -1 　　　 B.9 ， -1 　　 C.-1 ， 3 　　　 D.-1 ， 9 2 ．曲线 y= x 3 -2 在点 (1 ， ) 处切线的倾斜角为 ( ) A.30° B.45° C.135° D.150° 【 解析 】 1. 选 A ．因为函数 f(x) 的图象在点 P 处的切线方程是 y=-x+8 ， 所以 f′(5)=-1 ， f(5)=3. 故选 A ． 2. 选 B.Δy= (1+Δx) 3 -2-( ×1-2) = (Δx) 3 +Δx+(Δx) 2 ， 设倾斜角为 α ，则 tan α=1 ， 又 0°≤α ＜ 180° ，所以 α=45°. 知识点 2 导函数的概念 “ 函数 f(x) 在点 x 0 处的导数 f′(x 0 ) ”“ 导函数 f′(x) ”“ 导数 ” 之间的区别与联系 (1) 函数在一点处的导数 f′(x 0 ) ，就是在该点处函数值的改变量与自变量的改变量之比的极限值，它是一个常数，不是变数 . (2) 函数的导数是对某一区间内任意点 x 而言的，就是函数 f(x) 的导函数 f′(x). (3) 函数 f(x) 在点 x 0 处的导数 f′(x 0 ) 就是导函数 f′(x) 在 x=x 0 处的函数值，即 f′(x 0 )= 这也是求函数在点 x 0 处的导数的方法之一 . 【 微思考 】 任何一个函数都有导函数吗 ? 提示： 不是 . 比如函数 y=2x ， x∈{1 ， 2 ， 3} 就没有导函数 . 【 即时练 】 若 f(x) 是在 (-1 ， 1) 内的可导奇函数，且 f′(x) 不恒为 0 ，则 f′(x)( 　　 ) A. 必为 (-1 ， 1) 内的奇函数 B. 必为 (-1 ， 1) 内的偶函数 C. 必为 (-1 ， 1) 内的非奇非偶函数 D. 可能为奇函数也可能为偶函数 【 解析 】 选 B. 因为 f(x) 在 (-1 ， 1) 内可导，所以对任意 x∈ (-1 ， 1) ， f′(-x)= 又因为 f(x) 为奇函数，所以 f ［ -(x-Δx) ］ =-f(x-Δx) ， f(-x)=-f(x) ， 于是 f′(-x)= 所以 f′(x) 是 (-1 ， 1) 内的偶函数．故选 B ． 【 题型示范 】 类型一 求过曲线上一点的切线的方程 【 典例 1】 (1) 抛物线 f(x)=x 2 -3x+1 在点 (1 ， -1) 处的切线方程 为 ( 　　 ) A.y=-x-1 B.y=x C.y=-x D.y=x+1 (2) 已知曲线 y= 和这条曲线上的一点 P(2 ， ) ，判断曲线 y= 在点 P 处是否有切线，如果有，求出切线方程 . 【 解题探究 】 1. 题 (1) 中求曲线上一点的切线方程的关键是什么 ? 2. 题 (2)① 曲线 y= 在 x=2 处的导数的意义是什么 ? ② 过点 P(x 0 ， y 0 ) ，斜率为 k 的切线方程是什么 ? 【 探究提示 】 1. 关键是求曲线上切点处切线的斜率，即求该点的导数 . 2.① 曲线 y= 在 x=2 处的导数就是该点切线的斜率 . ② 切线方程是 y-y 0 =k(x-x 0 ). 【 自主解答 】 (1) 选 C. 当 Δx 趋于 0 时，得切线斜率 k=-1 ，切线方程为 y+1=-(x-1) ，即 y=-x ，故选 C. (2) 在曲线 y= 上点 P 附近取一点 Q. 设 Q 点的横坐标为 2+Δx ，则点 Q 的纵坐标为 所以，函数的增量 所以，割线 PQ 的斜率 所以 这表明曲线 y= 在点 P 处有 切线，且切线的斜率是 ，由点斜式可得切线方程为 即 【 方法技巧 】 1. 过曲线上一点求切线方程的三个步骤 2. 求过曲线 y=f(x) 外一点 P(x 1 ， y 1 ) 的切线方程的六个步骤 (1) 设切点 (x 0 ， f(x 0 )). (2) 利用所设切点求斜率 k=f′(x 0 )= (3) 用 (x 0 ， f(x 0 )) ， P(x 1 ， y 1 ) 表示斜率 . (4) 根据斜率相等求得 x 0 ，然后求得斜率 k. (5) 根据点斜式写出切线方程 . (6) 将切线方程化为一般式 . 【 变式训练 】 求曲线 y=f(x)=x 2 +1 过点 P(1 ， 0) 的切线方程 . 【 解析 】 设切点为 Q(a ， a 2 +1) ， 当 Δx 趋于 0 时， (2a+Δx) 趋于 2a ，所以，所求切线的斜率为 2a. 因此， 解得 a=1± ，所求的切线方程为 或 y= 【 误区警示 】 应注意题目中所给的点是否在曲线上，不要误以为所给的点都在曲线上而造成错误 . 【 补偿训练 】 1. 已知函数 f(x) 在 R 上满足 f(x)=2f(2-x)-x 2 +8x-8 ，则曲线 y=f(x) 在点 (1 ， f(1)) 处的切线方程是 __________. 【 解析 】 因为 f(x)=2f(2-x)-x 2 +8x-8 ， 所以 f(2-x)=2f(x)-(2-x) 2 +8(2-x)-8 ， 所以 f(2-x)=2f(x)-x 2 +4x-4+16-8x-8. 将 f(2-x) 代入 f(x)=2f(2-x)-x 2 +8x-8 得 f(x)=4f(x)-2x 2 -8x+8-x 2 +8x-8. 所以 f(x)= x 2 ， f′(x)=2x ， 所以 y=f(x) 在 (1 ， f(1)) 处的切线斜率为 2. 所以函数 y=f(x) 在 (1 ， f(1)) 处的切线方程为 y-1=2(x-1) ，即 y=2x-1. 答案： y=2x-1 2. 求函数 f(x)= +1 在点 (-1 ， -1) 处的切线方程 . 【 解析 】 f′(-1)= 故切线方程为 y+1=-2(x+1) ，即 2x+y+3=0. 类型二 求切点的坐标 【 典例 2】 (1) 若抛物线 y=x 2 +1 的一条切线与直线 y=2x-1 平行，则切点坐标为 ( 　　 ) A.(1 ， 1) 　　　 B.(1 ， 2) 　　　 C.(2 ， 5) 　　　 D.(3 ， 10) (2)(2014· 启东高二检测 ) 已知曲线 的一条切线的斜率为 ，则切点的坐标为 _______. 【 解题探究 】 1. 题 (1) 中由切线与直线平行能得到什么 ? 2. 题 (2) 中曲线上一点切线的斜率与该点的导数有什么关系 ? 【 探究提示 】 1. 切线与直线平行说明直线的斜率就是切点的导数 . 2. 曲线上一点切线的斜率就是该点的导数 . 【 自主解答 】 (1) 选 B. 平均变化率 所以斜率 k=2x=2 ，得 x=1 ， y=2. 故选 B. (2) 因为 y= ，所以 令 得 x=1 ，所以切点的坐标为 (1 ， ). 答案： (1 ， ) 【 延伸探究 】 若把题 (2) 中的“一条切线的斜率为 ”变为“一条切线与直线 x-y=0 垂直”，结果如何 ? 【 解析 】 因为 ，所以 y′= 因为所求切线与直线 x-y=0 垂直，所以切线的斜率为 -1 ， 令 =-1 ，得 x=-2 ，所以切点的坐标为 (-2 ， 1). 答案： (-2 ， 1) 【 方法技巧 】 1. 求切点坐标的五个步骤 (1) 先设切点坐标 (x 0 ， y 0 ). (2) 求导函数 f′(x). (3) 求切线的斜率 f′(x 0 ). (4) 由斜率间的关系列出关于 x 0 的方程，解方程求 x 0 . (5) 点 (x 0 ， y 0 ) 在曲线 f(x) 上，将 (x 0 ， y 0 ) 代入求 y 0 ，得切点坐标 . 2. 切点问题的处理策略 (1) 借斜率先求横坐标：由条件得到直线的倾斜角或斜率，由这些信息得知函数在某点的导数，进而求出点的横坐标 . (2) 与几何知识相联系：解决这些问题要注意和解析几何的知识联系起来，如直线的倾斜角和斜率的关系，两直线平行或垂直与斜率的关系等 . 【 变式训练 】 曲线 y=x 2 +1 在点 P(x 0 ， y 0 ) 的切线斜率为 2 ，求点 P(x 0 ， y 0 ) 的坐标 . 【 解析 】 设 f(x)=x 2 +1 ，则 =Δx+2x 0 ， 当 Δx→0 时， 令 2x 0 =2 ，解得 x 0 =1. 所以点 P 的坐标为 (1 ， 2). 【 补偿训练 】 点 P 是曲线 y=x 2 上任意一点，则点 P 到直线 y=x-6 的最小距离为 ___________ ． 【 解析 】 y′=2x ，令 2x=1 ，得 x= ，故 P( ) ，所以点 P 到 直线 y=x-6 的最小距离为 答案： 类型三 导数几何意义的应用 【 典例 3】 (1) 曲线 y= 和 y=x 2 在它们交点处的两条切线与 x 轴所围成的三角形的面积是 ________. (2) 求抛物线 C 1 ： y=x 2 +2x 与抛物线 C 2 ： y=-x 2 - 的公切线方程 . 【 解题探究 】 1. 题 (1) 中已知曲线方程，如何求两条曲线的交点坐标 ? 2. 题 (2) 中由公切线的意义需要建立什么方程 ? 【 探究提示 】 1. 把两条曲线的方程联立，方程组的解就是交点的坐标 . 2. 设公切线与抛物线 C 1 ： y=x 2 +2x 的切点为 (x 0 ， y 0 ) ，与抛物线 C 2 ： y=-x 2 - 的切点为 (x 1 ， y 1 ) ，由公切线的意义，建立方程组求出一个切点坐标即可 . 【 自主解答 】 (1) 由 得 所以曲线 y= 和 y=x 2 的交点坐标是 (1 ， 1) ， y= 的导数为 所以 y′| x=1 =-1 ，切线的方程是 y=-x+2 ， y=x 2 的导数为 ， y′| x=1 =2 ，切线方程为 y=2x-1 ，两 条切线与 x 轴的交点坐标分别为 (2 ， 0) 和 ( ， 0) ，故它们与 x 轴所围成的三角形的面积 答案： (2) 对 y=x 2 +2x 求导，根据导数的定义可得， y′=2x+2 ，对 y= -x 2 - 求导，根据导数的定义可得， y′=-2x ，设公切线与抛物线 C 1 ： y=x 2 +2x 的切点为 (x 0 ， y 0 ) ，与抛物线 C 2 ： y=-x 2 - 的切点为 (x 1 ， y 1 ) ，依题意可得方程组 y 1 -y 0 =(2x 0 +2)(x 1 -x 0 ) ， x 1 =-x 0 -1 ， y 0 =x 0 2 +2x 0 ， y 1 =-x 1 2 - 解得 x 0 =- ， y 0 =- 所以公切线方程为 即 4x-4y-1=0. 【 方法技巧 】 利用导数的几何意义处理综合应用题的两种思路 (1) 与导数的几何意义相关的题目往往涉及解析几何的相关知识，如直线的方程、直线间的位置关系等，因此要综合应用所学知识解题 . (2) 与导数的几何意义相关的综合问题解题的关键是函数在某点处的导数，已知切点可以求斜率，已知斜率也可以求切点，切点的坐标是常设的未知量 . 【 变式训练 】 (2014· 天津高二检测 ) 设点 P 是曲线 上的任意一点， P 点处的切线倾斜角为 α ，则 α 的取值范围为 ____________. 【 解析 】 设 P(x 0 ， y 0 ) ， 因为 所以切线的斜率 所以 所以 答案： 【 补偿训练 】 点 A(x 1 ， y 1 ) ， B(x 2 ， y 2 ) 是抛物线 C ： x 2 =2y 上的不同两点，过 A ， B 分别作抛物线 C 的切线，两条切线交于点 P(x 0 ， y 0 ) ． 求证： x 0 是 x 1 与 x 2 的等差中项 . 【 证明 】 对 y= x 2 求导，根据导数的定义可得 y′=x ， 所以直线 PA ： y=x 1 (x-x 1 )+y 1 ，即 y=x 1 x- x 1 2 ， 同理，直线 PB ： y=x 2 x- x 2 2 ， 因为两条切线交于点 P(x 0 ， y 0 ) ， 所以令 x 1 x- x 1 2 =x 2 x- x 2 2 ， 解得 x 0 = 所以 x 0 是 x 1 与 x 2 的等差中项 . 【 规范解答 】 用导数的定义求切线的方程 【 典例 】 (12 分 )(2014 · 郑州高二检测 ) 已知函数 f(x)=x 3 -3x 及 y=f(x) 上一点 P(1 ， -2) ，求过点 P 与曲线 y=f(x) 相切的直线方程 . 【 审题 】 抓信息，找思路 【 解题 】 明步骤，得高分 【 点题 】 警误区，促提升 失分点 1 ：若不能正确地求出①处的导数，弄错切线的斜率，会导致本例不得分 . 失分点 2 ：若漏掉②处，误认为点 (1 ， -2) 为切点，造成解题思路错误，从而仅求得一条切线，本例最多得 5 分 . 失分点 3 ：若不能正确地得到③式，即没能正确地写出过点 (x 0 ， x 0 3 -3x 0 ) 的直线方程，则不能求出 x 0 的两个值，此种情况最多得 4 分 【 悟题 】 提措施，导方向 1. 记清常用的公式 利用导数的定义求曲线上某一点的导数，要记清导数的表达式，化简后求极限时的式子要有意义，如本例中求得 y′=3x 2 -3. 2. 理清切点的实质 在求切线方程的过程中，关键是寻找两个条件：一是切点，二是切线的斜率 . 其中切点又是关键，需要找清切点，如本例中点 P(1 ， -2) 不一定是切点，做题时要高度关注 . 【 类题试解 】 求抛物线 y=x 2 过点 ( ， -6) 的切线方程 . 【 解析 】 由于点 ( ， -6) 不在抛物线上，可设切点为 (x 0 ， x 0 2 ) ， 所以切线的斜率为 2x 0 ， 又因为此切线过点 ( ， -6) 和点 (x 0 ， x 0 2 ) ， 所以 即 x 0 2 +5x 0 -6=0. 解得 x 0 =-6 或 x 0 =1. 因此过点 (-6 ， 36) ， (1 ， 1) 的切线方程分别为 y-36=-12(x+6) 和 y-1=2(x-1) ，即 12x+y+36=0 和 2x-y-1=0.