专题1-7 排列组合二项式定理（讲）-2018年高考数学（理）二轮复习讲练测

专题1-7 排列组合二项式定理（讲）-2018年高考数学（理）二轮复习讲练测

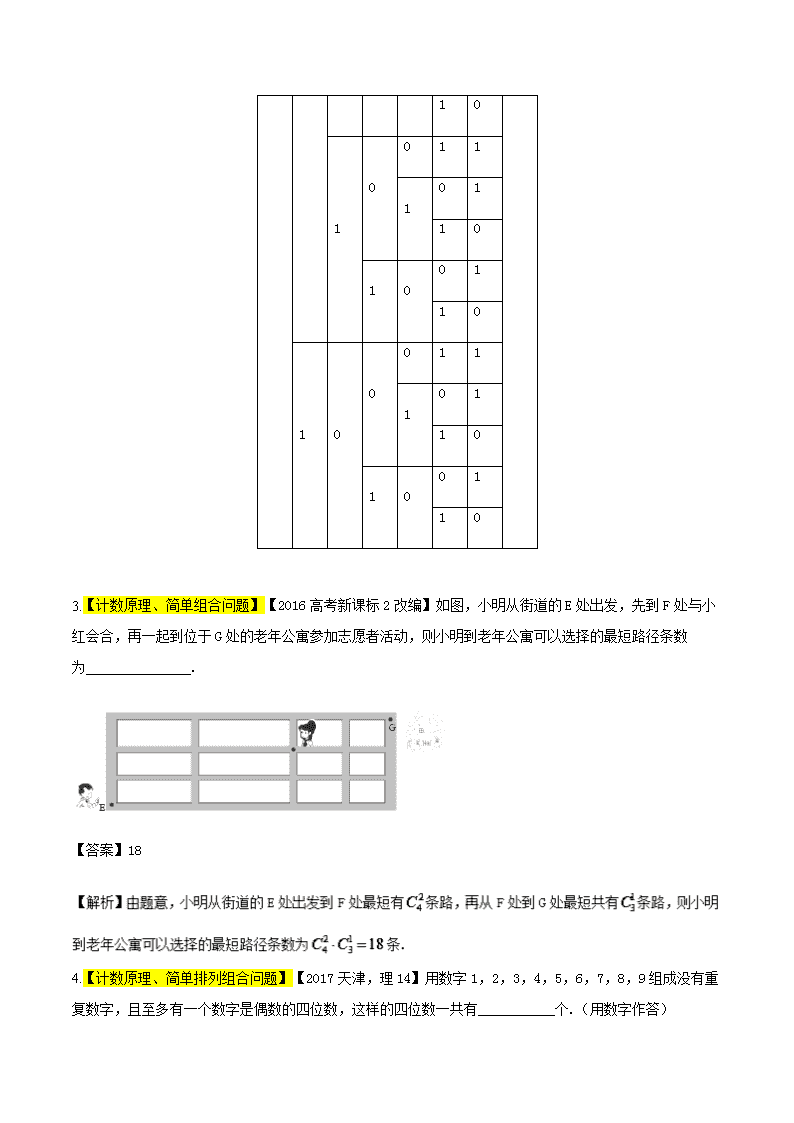
‎2018年高三二轮复习讲练测之讲案【新课标版理科数学】‎ 讲---高效整合 专题七 排列组合二项式定理 考向一 两个计数原理、排列组合的综合应用 ‎【高考改编☆回顾基础】‎ ‎1.【计数原理、简单排列组合问题】【2017课标II改编】安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有 .‎ ‎【答案】36‎ ‎2.【两个计数原理】【2016高考新课标3改编】定义“规范01数列”如下：共有项，其中项为0，项为1，且对任意，中0的个数不少于1的个数.若，则不同的“规范01数列”共有 .‎ ‎【答案】14‎ ‎【解析】由题意，得必有，，则具体的排法列表如下：‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎3.【计数原理、简单组合问题】【2016高考新课标2改编】如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为 .‎ ‎【答案】18‎ ‎4.【计数原理、简单排列组合问题】【2017天津，理14】用数字1，2，3，4，5，6，7，8，9组成没有重复数字，且至多有一个数字是偶数的四位数，这样的四位数一共有___________个.（用数字作答）‎ ‎【答案】 ‎ ‎【解析】.‎ ‎【命题预测☆看准方向】‎ 从近五年高考试题来看,高考命题对排列组合注重基础知识和基本解题方法、规律的考查以及运算能力的考查.题目的难度基本都为中等或中等以下.考查的重点重点，一是利用计数原理、排列、组合知识进行计数；二是与概率问题的综合等.‎ ‎【典例分析☆提升能力】‎ ‎【例1】【2018届山东省师大附中高三第三次模拟】将编号的小球放入编号为盒子中,要求不允许有空盒子,且球与盒子的编号不能相同,则不同的放球方法有（ ）‎ A. 种 B. 种 C. 种 D. 种 ‎【答案】C ‎【解析】由题意可知,这四个小球有两个小球放在一个盒子中,当四个小球分组为如下情况时,放球方法有:‎ 当1与2号球放在同一盒子中时,有2种不同的放法;‎ 当1与3号球放在同一盒子中时,有2种不同的放法;‎ 当1与4号球放在同一盒子中时,有2种不同的放法;‎ 当2与3号球放在同一盒子中时,有2种不同的放法;‎ 当2与4号球放在同一盒子中时,有2种不同的放法;‎ 当3与4号球放在同一盒子中时,有2种不同的放法;‎ 因此,不同的放球方法有12种.‎ 故选：C ‎【趁热打铁】【2018届辽宁省沈阳市郊联体高三上学期期末】‎ 高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践，但去何工厂可自由选择，甲工厂必须有班级要去，则不同的分配方案有（ ）‎ A. 16种 B. 18种 C. 37种 D. 48种 ‎【答案】C ‎【例2】【2018届北京市西城区高三期末】把件不同的产品摆成一排．若其中的产品与产品都摆在产品的左侧，则不同的摆法有____种．（用数字作答）‎ ‎【答案】8‎ ‎【解析】当 在最右边位置时，由 种排法符合条件；当在从右数第二个位置时，由种排法符合条件，把件不同的产品摆成一排．若其中的产品与产品都摆在产品的左侧，则不同的摆法有种，故答案为.‎ ‎【趁热打铁】【2018届湖南师范大学附属中学高三上学期月考（五）】某班上午有五节课，分别安排语文，数学，英语，物理，化学各一节课．要求语文与化学相邻，数学与物理不相邻，且数学课不排第一节，则不同排课法的种数是（ ）‎ A. 16 B. 24 C. 8 D. 12‎ ‎【答案】A ‎【例3】【2017年12月浙江省重点中学期末热身联考】甲，乙，丙，丁四名同学做传递手帕游戏（每位同学传递到另一位同学记传递1次），手帕从甲手中开始传递，经过5次传递后手帕回到甲手中，则共有__________种不同的传递方法．（用数字作答）‎ ‎【答案】种 ‎【解析】根据题意分3种情况 ‎①当甲第一次传给其余3人，有种情况，第二次将手帕传给了甲，第三次甲再传给其余3人，有种情况，第四次传给了除甲以外的2人，有种情况，第五次传给甲，此时有种情况；‎ ‎②当甲第一次传给其余3人，有种情况，第二次将手帕传给了除甲以外的2人，有种情况，第三次传给了甲，第四次传给了其余3人，有种情况， 第五次传给甲，此时有种情况；‎ ‎③当甲第一次传给其余3人，有种情况，第二次将手帕传给了除甲以外的2人，有种情况，第三次再传给了除甲以外的2人，有种情况，第四次仍然传给了除甲以外的2人，有种情况，第五次传给甲，此时有种情况 综上，共有种不同的传递方法 故答案为60.‎ ‎【趁热打铁】8人排成一排照相，分别求下列条件下的不同照相方式的种数.‎ ‎（1）其中甲、乙相邻，丙、丁相邻；‎ ‎（2）其中甲、乙不相邻，丙、丁不相邻；‎ ‎（要求写出解答过程，并用数字作答）‎ ‎【答案】(1)2880(2)23040‎ ‎【解析】试题分析：（1）相邻问题用捆绑法：即将甲、乙看作一个元素，丙、丁相邻看作一个元素，这样六个元素全排列，再分别乘以甲、乙排列数以及丙、丁排列数（2）不相邻问题用插空法：先排剩下六人全排列，再插空排甲、乙得甲、乙不相邻的排法总数，最后减去甲、乙不相邻时但丙、丁相邻的情况即得结果 试题解析：（1）捆绑法，共有种不同排法.‎ ‎（2）间接法，先求出甲、乙不相邻的排法总数，再减去甲、乙不相邻时但丙、丁相邻的情况，此时有种，故共有种.‎ ‎【方法总结☆全面提升】‎ ‎1.在分类加法计数原理中,每一种方法都能完成这件事情,类与类之间是相互独立的,不能重复.即分类的标准是“不重不漏,一步完成”.‎ ‎2.在分步乘法计数原理中,各个步骤相互依存,在各个步骤中任取一种方法,即是完成这个步骤的一种方法.‎ ‎3.应用两种原理解题要注意分清要完成的事情是什么,完成该事情是分类完成还是分步完成.分类的就应用分类加法计数原理,分步的就应用分步乘法计数原理;在综合应用两个原理时,一般先分类再分步,在每一步当中又可能用到分类加法计数原理.‎ ‎4.解决排列组合问题的基本方法有: 解决排列问题的主要方法 ‎(1)解决“在”与“不在”的有限制条件的排列问题，既可以从元素入手，也可以从位置入手，原则是谁“特殊”谁优先．不管是从元素考虑还是从位置考虑，都要贯彻到底，不能既考虑元素又考虑位置．‎ ‎(2)解决相邻问题的方法是“捆绑法”，即把相邻元素看做一个整体和其他元素一起排列，同时要注意捆绑元素的内部排列．‎ ‎(3)解决不相邻问题的方法是“插空法”，即先考虑不受限制的元素的排列，再将不相邻的元素插在前面元素排列的空当中．‎ ‎(4)对于定序问题，可先不考虑顺序限制，排列后，再除以定序元素的全排列．‎ ‎(5)若某些问题从正面考虑比较复杂，可从其反面入手，即采用“间接法”．‎ ‎【规范示例☆避免陷阱】‎ ‎【典例】要从12人中选出5人去参加一项活动，按下列要求，有多少种不同选法？‎ ‎(1)A，B，C,3人都参加；‎ ‎(2)A，B，C,3人都不参加；‎ ‎(3)A，B，C,3人中只有一个参加．‎ ‎【规范解答】(1)只需再从A，B，C之外的9人中选择2人，‎ 所以有方法＝36(种)．‎ ‎(2)由于A，B，C三人都不能入选，所以只能从余下的9人中选择5人，即有选法＝126(种)．‎ ‎(3)可分两步：先从A，B，C三人中选出一人，有种选法；再从其余的9人中选择4人，有种选法．‎ 所以共有选法 (种)．‎ ‎【反思提高】解排列、组合的应用题，通常有以下途径：‎ ‎(1)以元素为主体，即先满足特殊元素的要求，再考虑其他元素．‎ ‎(2)以位置为主体，即先满足特殊位置的要求，再考虑其他位置．‎ ‎(3)先不考虑附加条件，计算出排列或组合数，再减去不符合要求的排列或组合数．‎ ‎【误区警示】‎ 解答排列组合应用题要从“分析”“分辨”“分类”“分步”的角度入手.‎ ‎(1)“分析”就是找出题目的条件、结论,哪些是“元素”,哪些是“位置”;‎ ‎(2)“分辨”就是辨别是排列还是组合,对某些元素的位置有无限制等;‎ ‎(3)“分类”就是首先对于较复杂问题中的元素分成互斥的几类,然后逐类解决;‎ ‎(4)“分步”就是首先把问题化成几个互相联系的步骤,而每一步都是简单的排列组合问题,然后逐步解决.考向二 二项式定理 ‎【高考改编☆回顾基础】‎ ‎1.【二项式定理求指定项系数】【新课标1，改编】展开式中的系数为 .‎ ‎【答案】30 ‎ ‎2．【二项式定理由指定项系数求n】【2017山东，理11】已知的展开式中含有项的系数是，则 .‎ ‎【答案】‎ ‎【解析】试题分析：由二项式定理的通项公式，令得：，解得．‎ ‎3. 【虚数单位、二项式定理求指定项】【2016年高考四川改编】设i为虚数单位，则的展开式中含x4的项为 .‎ ‎【答案】－15x4‎ ‎【解析】二项式展开的通项，令，得，则展开式中含的项为.‎ ‎4. 【二项式定理由指定项系数求参数值】【2016高考山东理数】若（ax2+）5的展开式中x5的系数是—80，则实数a=_______.‎ ‎【答案】-2‎ ‎【解析】因为，所以由，因此 ‎【命题预测☆看准方向】‎ 从近五年高考试题来看,高考命题对排二项式定理注重基础知识和基本解题方法、规律的考查以及运算能力的考查.题目的难度基本都为中等或中等以下.考查的重点重点是求二项展开式中的某一项的二项式系数、指定项、各项系数和、n的值、参数的值等.‎ ‎【典例分析☆提升能力】‎ ‎【例1】【2018届黑龙江省七台河市高三上期末】已知展开式的所有项系数之和为81，则的常数项为__________．‎ ‎【答案】-2‎ ‎【解析】因为展开式的所有项系数之和为81，所以，解得，所以中的常数项为，故填.‎ ‎【趁热打铁】【2018届四川省成都市龙泉中学高三12月月考】的展开式中的常数项为___________.（用数字作答）‎ ‎【答案】‎ ‎【例2】【2018届河北省鸡泽县第一中学高三上学期第四次月考】展开式中含项的系数为_______.（用数字表示）‎ ‎【答案】0‎ ‎【解析】∵（x+1）（x﹣1）5 ‎ ‎=（x+1）（ x5+++++），‎ 故展开式中含x3 的项的系数为﹣+=0，‎ 故答案为 0．‎ ‎【趁热打铁】【2018届辽宁省凌源市高三上期末】的展开式中，含的项的系数为__________．‎ ‎【答案】‎ ‎【解析】通项为 令，解得： ，故含的项的系数为.‎ 故答案为： ‎ ‎【例3】【2018届安徽省皖南八校高三12月联考】若， 展开式中， 的系数为-20，则等于 A. -1 B. C. -2 D. ‎ ‎【答案】A ‎【解析】由，可得将选项中的数值代入验证可得， 符合题意，故选A.‎ ‎【趁热打铁】在的展开式中，若存在常数项，则n的最小值是(　　)‎ A. 3 B. 5 C. 8 D. 10‎ ‎【答案】B ‎【方法总结☆全面提升】‎ ‎1. 求二项展开式中的指定项,一般是利用通项公式进行化简,令字母的指数符合要求(求常数项时,指数为零;求有理项时,指数为整数等),解出项数r+1,代回通项公式即可. ‎ ‎2. 二项式定理给出的是一个恒等式,对于a,b的一切值都成立.因此,可将a,b设定为一些特殊的值.在使用赋值法,令a,b等于多少时,应视具体情况而定,一般取“1,-1或0”,有时也取其他值.‎ ‎ 3. 一般地,若f(x)=a0+a1x+a2x2+…+anxn ‎,则f(x)的展开式中各项系数之和为f(1),奇数项系数之和为a0+a2+a4+…=,偶数项系数之和为a1+a3+a5+…=.‎ ‎【规范示例☆避免陷阱】‎ ‎【典例】设,若a1+a2+…+an=63,则展开式中系数最大的项是(　　)‎ A.15x2 B.20x3 C.21x3 D.35x3‎ ‎【反思提升】二项展开式系数最大的项的求法:‎ 求(a+bx)n(a,b∈R)的展开式系数最大的项,一般是采用待定系数法,设展开式中各项系数分别为A1,A2,…,An+1,且第r项系数最大,应用 解出r,即得展开式系数最大的项.要特别注意二项式系数与二项展开式系数的区别.‎ ‎【误区警示】应用通项公式要注意五点:‎ ‎(1)它表示二项展开式的任意项,只要n与r确定,该项就随之确定;‎ ‎(2)Tr+1是展开式中的第(r+1)项,而不是第r项;‎ ‎(3)公式中a,b的指数和为n,且a,b不能随便颠倒位置;‎ ‎(4)要将通项中的系数和字母分离开,以便于解决问题;‎ ‎(5)对二项式(a-b)n展开式的通项公式要特别注意符号问题.‎