2019届二轮复习常考题型答题技巧变量间的相关关系学案（全国通用）

2019届二轮复习常考题型答题技巧变量间的相关关系学案（全国通用）

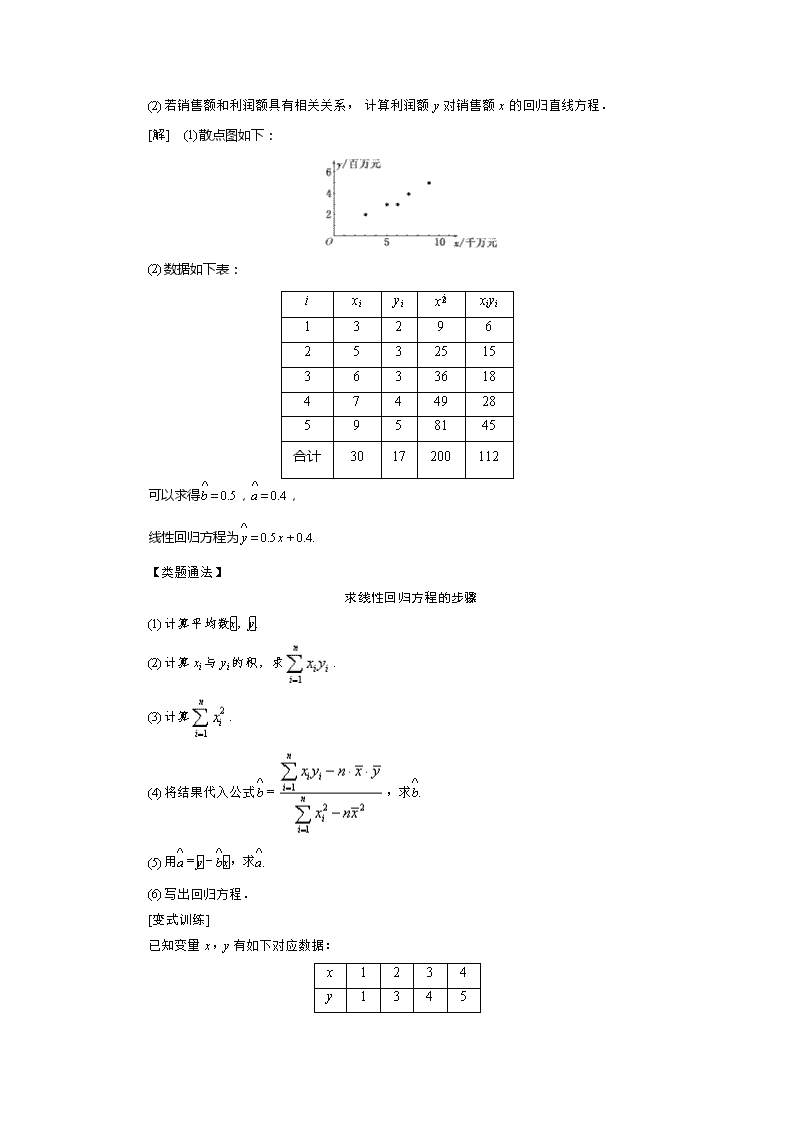
‎2019届二轮复习 常考题型答题技巧 变量间的相关关系 学案 （全国通用）‎ ‎【知识梳理】‎ ‎1．相关关系 如果两个变量中一个变量的取值一定时，另一个变量的取值带有一定的随机性，那么这两个变量之间的关系叫做相关关系．‎ ‎2．散点图 将各数据在平面直角坐标系中的对应点画出来，得到表示两个变量的一组数据的图形，这样的图形叫做散点图，利用散点图，可以判断两个变量是否相关，相关时是正相关还是负相关．‎ ‎3．正相关和负相关 ‎(1)正相关：散点图中的点散布在从左下角到右上角的区域．‎ ‎(2)负相关：散点图中的点散布在从左上角到右下角的区域．‎ ‎4．回归直线方程 ‎(1)回归直线：如果散点图中点的分布从整体上看大致在一条直线附近，就称这两个变量之间具有线性相关关系，这条直线叫做回归直线．‎ ‎(2)回归方程：回归直线的方程，简称回归方程．‎ ‎(3)回归方程的推导过程：‎ ‎①假设已经得到两个具有线性相关关系的变量的一组数据(x1，y1)，(x2，y2)，…，(xn，yn)．‎ ‎②设所求回归方程为＝x＋，其中，是待定参数．‎ ‎③由最小二乘法得 ‎　　. ]‎ 其中：是回归方程的斜率，是截距．‎ ‎【常考题型】‎ 题型一、相关关系的判断 ‎【例1】　(1)下列关系中，属于相关关系的是 ‎ ‎①正方形的边长与面积之间的关系；‎ ‎②农作物的产量与施肥量之间的关系；‎ ‎③人的身高与年龄之间的关系；‎ ‎④降雪量与交通事故的发生率之间的关系．‎ ‎(2)某个男孩的年龄与身高的统计数据如下表所示.‎ 年龄(岁)x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 身高(cm)y ‎78‎ ‎87‎ ‎98‎ ‎108‎ ‎115‎ ‎120‎ ‎①画出散点图；‎ ‎②判断y与x是否具有线性相关关系．‎ ‎[解析]　(1)在①中，正方形的边长与面积之间的关系是函数关系；在②中，农作物的产量与施肥量之间不具有严格的函数关系，但具有相关关系；在③中，人的身高与年龄之间的关系既不是函数关系，也不是相关关系，因为人的年龄达到一定时期身高就不发生明显变化了，因而它们不具有相关关系；在④中，降雪量与交通事故的发生率之间具有相关关系．‎ ‎[答案]　(1)②④‎ ‎(2)①散点图如图所示．‎ ‎②由图知，所有数据点接近一条直线排列，因此，认为y与x有线性相关关系．‎ ‎【类题通法】‎ 两个变量是否相关的两种判断方法 ‎(1)根据实际经验：借助积累的经验进行分析判断．‎ ‎(2)利用散点图：通过散点图，观察它们的分布是否存在一定的规律，直观地进行判断．‎ ‎【对点训练】‎ 如图所示的两个变量不具有相关关系的有 ．‎ 解析：①是确定的函数关系；②中的点大都分布在一条曲线周围；③中的点大都分布在一条直线周围；④中点的分布没有任何规律可言，x，y不具有相关关系．‎ 答案：①④‎ 题型二、求回归方程 ‎【例2】　某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表：‎ 商店名称 A B C D E 销售额(x)/千万元 ‎3‎ ‎5‎ ‎6‎ ‎7‎ ‎9‎ 利润额(y)/百万元 ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎(1)画出销售额和利润额的散点图；‎ ‎(2)若销售额和利润额具有相关关系，计算利润额y对销售额x的回归直线方程．‎ ‎[解]　(1)散点图如下：‎ ‎(2)数据如下表：‎ i xi yi x xiyi ‎1‎ ‎3‎ ‎2‎ ‎9‎ ‎6‎ ‎2‎ ‎5‎ ‎3‎ ‎25‎ ‎15‎ ‎3‎ ‎6‎ ‎3‎ ‎36‎ ‎18‎ ‎4‎ ‎7‎ ‎4‎ ‎49‎ ‎28‎ ‎5‎ ‎9‎ ‎5‎ ‎81‎ ‎45‎ 合计 ‎30‎ ‎17‎ ‎200‎ ‎112‎ 可以求得＝0.5，＝0.4，‎ 线性回归方程为＝0.5x＋0.4.‎ ‎【类题通法】‎ 求线性回归方程的步骤 ‎(1)计算平均数，.‎ ‎(2)计算xi与yi的积，求.‎ ‎(3)计算.‎ ‎(4)将结果代入公式＝，求.‎ ‎(5)用＝－，求.‎ ‎(6)写出回归方程．‎ ‎[变式训练]‎ 已知变量x，y有如下对应数据：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ y ‎1‎ ‎3‎ ‎4‎ ‎5‎ ‎(1)作出散点图；‎ ‎(2)用最小二乘法求关于x，y的回归直线方程．‎ 解：(1)散点图如图所示．‎ ‎(2)＝＝，‎ ＝＝， ]‎ yi＝1＋6＋12＋20＝39.‎ ‎＝1＋4＋9＋16＝30，‎ ＝＝，‎ ＝－×＝0，‎ 所以＝x为所求回归直线方程.‎ 题型三、利用线性回归方程对总体进行估计 ‎【例3】　一台机器由于使用时间较长，但还可以使用，它按不同的转速生产出来的某机器零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，下表是抽样试验结果：‎ 转速x(转/秒)(x∈N )‎ ‎16 ‎ ‎14‎ ‎12‎ ‎8‎ 每小时生产有缺点的零件数y(件)‎ ‎11‎ ‎9‎ ‎8‎ ‎5‎ ‎(1)如果y与x具有线性相关关系，求回归方程；‎ ‎(2)若实际生产中，允许每小时的产品中有缺点的零件数最多为10个，那么机器的转速应该控制在什么范围内？‎ ‎[解]　(1)由题意，可得＝12.5，＝8.25，yi＝438，＝660，则＝≈0.728 6，＝－＝－0.857 5.‎ 所以回归直线的方程为＝0.728 6x－0.857 5.‎ ‎(2)要使y≤10，则0.728 6x－0.857 5≤10，‎ 解得x≤14.90.所以机器的转速应该控制在15转/秒以下．‎ ‎【类题通法】‎ 回归分析的三个步骤 ‎(1)进行相关性检验，若两变量无线性相关关系，则所求的线性回归方程毫无意义．‎ ‎(2)求回归直线方程，其关键是正确地求得，.‎ ‎(3)根据直线方程进行预测．‎ ‎【对点训练】‎ 假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)，有如下的统计资料：‎ 使用年限x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 维修费用y ‎2.2‎ ‎3.8‎ ‎5.5‎ ‎6.5‎ ‎7. 0‎ 由资料可知y与x具有相关关系．‎ ‎(1)求回归方程＝x＋的回归系数，；‎ ‎(2)估计使用年限为10年时维修费用是多少．‎ 解：(1)先把数据列成表.‎ 序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎  xi ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎20‎ yi ‎2.2‎ ‎3.8‎ ‎5.5‎ ‎6.5‎ ‎7.0‎ ‎25‎ xiyi ‎4.4‎ ‎11.4‎ ‎22.0‎ ‎32.5‎ ‎42.0‎ ‎112.3‎ x ‎4‎ ‎9‎ ‎16‎ ‎25‎ ‎36‎ ‎90‎ 由表可知＝4，＝5，由公式可得：‎ ＝＝＝1.23，‎ ＝－＝5－1.23×4＝0.08.‎ ‎(2)由(1)可知回归方程是＝1.23x＋0.08，‎ ‎∴当x＝10时，＝1.23×10＋0.08＝12.3＋0.08＝12.38(万元)．‎ 故估计使用年限为10年时，维修费用是12.38万元．‎ ‎【练习反馈】‎ ‎1．下列命题正确的是(　　) ]‎ ‎①任何两个变量都具有相关关系；‎ ‎②圆的周长与该圆的半径具有相关关系；‎ ‎③某商品的需求量与该商品的价格是一种非确定性关系；‎ ‎④根据散点图求得的回归直线方程可能是没有意义的；‎ ‎⑤两个变量间的相关关系可以通过回归直线，把非确定性问题转化为确定性问题进行研究．‎ A．①③④　　　　　　　　 　B．②③④‎ C．③④⑤ D．②④⑤‎ 解析：选C　①显然不对，②是函数关系，③④⑤正确．‎ ‎2．对变量x，y有观测数据(xi，yi)(i＝1,2，…，10)，得散点图图1；对变量u，v有观测数据(ui，vi)(i＝1,2，…，10)，得散点图图2.由这两个散点图可以判断(　　)‎ A．变量x与y正相关，u与v正相关 B．变量x与y正相关，u与v负相关 C．变量x与y负相关，u与v正相关 D．变量x与y负相关，u与v负相关 解析：选C　由这两个散点图可以判断，变量x与y负相关，u与v正相关．‎ ‎3．若施肥量x(kg)与水稻产量y(kg)的线性回归方程为＝5x＋250，当施肥量为‎80 kg时，预计水稻产量约为 kg.‎ 解析：把x＝‎80 kg代入回归方程可得其预测值＝5×80＋250＝650(kg)．‎ 答案：650‎ ‎4．对具有线性相关关系的变量x和y，测得一组数据如下表所示.‎ x ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ 若已求得它们的回归直线的斜率为6.5，这条回归直线的方程为 ．‎ 解析：由题意可知＝＝5，‎ ＝＝50.‎ 即样本中心为(5,50)‎ 设回归直线方程为＝6.5x＋，‎ ‎∵回归直线过样本中心(，)，‎ ‎∴50＝6.5×5＋，即＝17.5，‎ ‎∴回归直线方程为＝6.5x＋17.5‎ 答案：＝6.5x＋17.5‎ ‎5．2013年元旦前夕，某市统计局统计了该市2012年10户家庭的年收入和年饮食支出的统计资料如下表：‎ 年收入 x(万元)‎ ‎2‎ ‎4‎ ‎4‎ ‎6‎ ‎6‎ ‎6‎ ‎7‎ ‎7‎ ‎8‎ ‎10‎ 年饮食支 出y(万元)‎ ‎0.9‎ ‎1.4‎ ‎1.6‎ ‎2.0‎ ‎2.1‎ ‎1.9‎ ‎1.8 , ,k ]‎ ‎2.1‎ ‎2.2‎ ‎2.3‎ ‎(1)如果已知y与x是线性相关的，求回归方程；‎ ‎(2)若某家庭年收入为9万元，预测其年饮食支出．‎ ‎(参考数据：＝117.7，＝406)‎ 解：依题意可计算得：‎ ＝6，＝1.83，2＝36， ＝10.98，‎ 又∵＝117.7，＝406，‎ ‎∴＝≈0.17，‎ ＝－＝0.81，‎ ‎∴＝0.17x＋0.81.‎ ‎∴所求的回归方程为＝0.17x＋0.81.‎ ‎(2)当x＝9时，＝0.17×9＋0.81＝2.34(万元)．‎ 可估计大多数年收入为9万元的家庭每年饮食支出约为2.34万元．‎