数学理卷·2018届山西省太原市第五中学高三下学期4月阶段性练习（一模）（2018

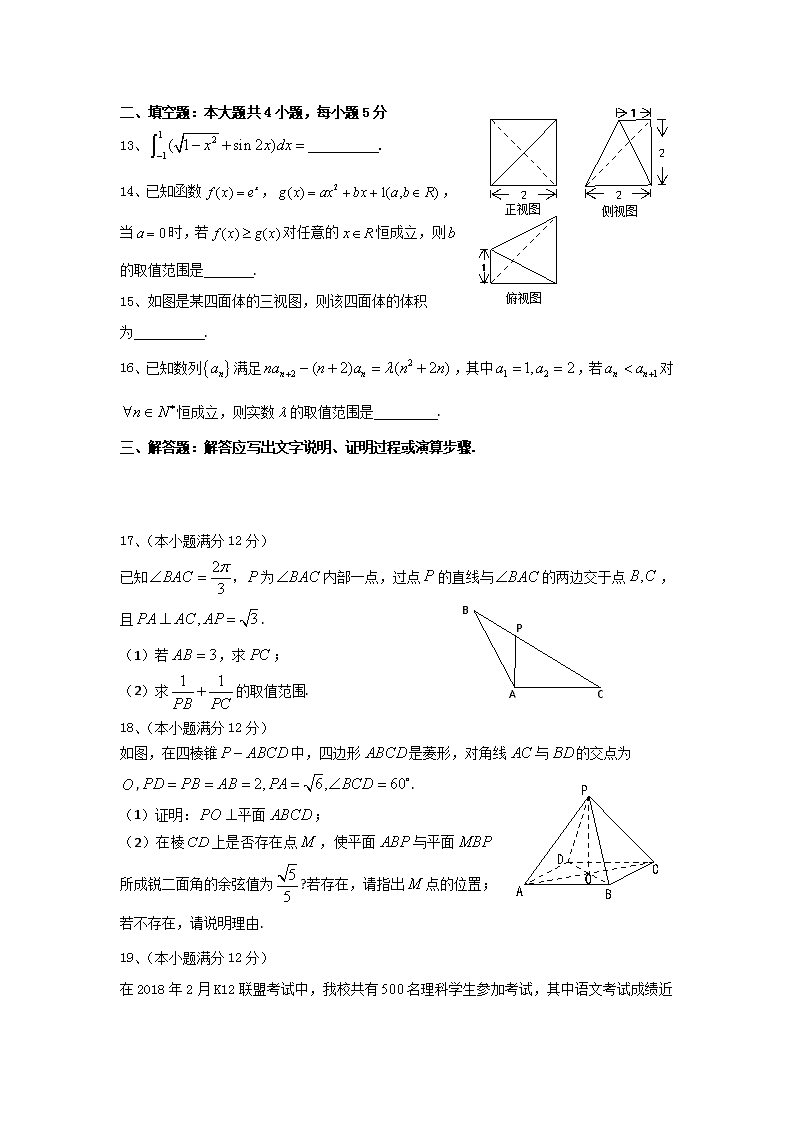
数学理卷·2018届山西省太原市第五中学高三下学期4月阶段性练习（一模）（2018

太原五中2017-2018学年度第二学期阶段性检测 高 三 数 学（理）‎ 出题人、校对人：刘晓瑜、郭舒平、董亚萍、刘锦屏、凌河、闫晓婷（2018.4.2）‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1、已知,则（ ）‎ ‎ ‎ ‎2、已知复数为虚数单位在复平面内对应的点在第三象限，则实数的取值范围是（ ）‎ ‎ ‎ ‎3、在中，角所对的边分别是，若直线与平行，则一定是（ ）‎ 锐角三角形 等腰三角形 直角三角形 等腰或直角三角形 ‎4、在区间随机地取一个数，则方程表示焦点在轴上的椭圆的概率是（ ）‎ ‎ ‎ ‎5、若的展开式中的二项式系数和为，则（ ）‎ ‎ ‎ ‎6、《算法统宗》是中国古代数学名著，由明代数学家程大位所著，该著作完善了珠算口诀，确立了算盘用法，完成了由筹算到珠算的彻底转变，对我国民间普及珠算和数学知识起到了很大的作用．如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题，执行该程序框图，若输出的的值为，则输入的的值为（ ）‎ ‎ ‎ ‎7、已知等比数列的前项和是，则下列说法一定成立的是（ ） ‎ 若，则 若，则 ‎ 若，则 若，则 ‎8、已知，点是直线与圆的公共点，则的最大值为（ ）‎ ‎ ‎ ‎9、若不等式组，所表示的平面区域存在点，使成立，则实数的取值范围是（ ）‎ ‎ ‎ ‎10、平行四边形中，，点在边上，则的最大值为（ ）‎ ‎ ‎ ‎11、已知是双曲线的左、右焦点，过的直线与双 曲线的左支交于点，与右支交于点，若，，则 ‎（ 　）‎ ‎ ‎ ‎12、不等式有且只有一个整数解，则的取值范围为（ ）‎ ‎ ‎ ‎ ‎ 第Ⅱ卷 本卷包括必考题和选考题两部分.第13题—第21题为必考题，每个试题考生都必须作答.第22题—第23题为选考题，考生根据要求作答.‎ 正视图 侧视图 俯视图 ‎1‎ ‎2‎ ‎2‎ ‎1‎ ‎2‎ 二、填空题：本大题共4小题，每小题5分 ‎13、 .‎ ‎14、已知函数，，当时，若对任意的恒成立，则的取值范围是 .‎ ‎15、如图是某四面体的三视图，则该四面体的体积为　　　　　.‎ ‎16、已知数列满足，其中，若对恒成立，则实数的取值范围是 .‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤.‎ ‎17、（本小题满分12分）‎ A C P B 已知为内部一点，过点的直线与的两边交于点，且.‎ ‎（1）若，求；‎ ‎（2）求的取值范围.‎ ‎18、（本小题满分12分）‎ 如图，在四棱锥中，四边形是菱形，对角线与的交点为 A P B C D O ‎,. ‎ ‎（1）证明：平面；‎ ‎（2）在棱上是否存在点，使平面与平面所成锐二面角的余弦值为?若存在，请指出点的位置；若不存在，请说明理由. ‎ ‎19、（本小题满分12分）‎ 在2018年2月K12联盟考试中，我校共有名理科学生参加考试 ‎，其中语文考试成绩近似服从正态分布，数学成绩的频率分布直方图如图：‎ ‎（1）如果成绩大于的为特别优秀，这名学生中本次考试语文、数学成绩特别优秀的大约各多少人？‎ ‎（2）如果语文和数学两科都特别优秀的共有人，从（1）中的这些同学中随机抽取人，设三人中两科都特别优秀的有人，求的分布列和数学期望．‎ ‎（3）根据以上数据，是否有以上的把握认为语文特别优秀的同学，数学也特别优秀？‎ ‎①若~，‎ 则 ‎②‎ ‎③‎ ‎0.50‎ ‎0.40‎ ‎…‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎0.455‎ ‎0.708‎ ‎…‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 数学成绩 ‎ ‎50 ‎ ‎70 ‎ ‎150 ‎ ‎130 ‎ ‎110 ‎ ‎90 ‎ ‎0.0012 ‎ ‎0.008‎ ‎0.0088 ‎ ‎0.024 ‎ 频率/组距 ‎20、（本小题满分12分）‎ 已知椭圆，为左焦点，为上顶点，为右顶点，‎ 若，抛物线的顶点在坐标原点，焦点为.‎ ‎（1）求的标准方程；‎ ‎（2）是否存在过点的直线，与和交点分别是，和，，使得 ‎？如果存在，求出直线的方程；如果不存在，请说明理由.‎ ‎21、（本小题满分12分）‎ 已知函数.‎ ‎（1）当时，讨论的极值情况；‎ ‎（2）若，求的值.‎ 请考生从第22、23 题中任选一题作答，并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所选涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分.‎ ‎22、（本小题满分10分）【选修4——4：坐标系与参数方程】‎ 在平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，并使得它与直角坐标系有相同的长度单位，曲线的极坐标方程为，曲线的极坐标方程为.‎ ‎（1）求曲线的普通方程和的直角坐标方程；‎ ‎（2）设分别交、于点、，求的面积.‎ ‎23、（本小题满分10分）【选修4——5：不等式选讲】‎ 已知函数.‎ ‎（1）当时，解不等式； ‎ ‎（2）若，且当时，不等式恒成立，求实数的取值范围．‎ 理科数学 参考答案 ‎1.B ‎2.C ‎3.C【解析】由两直线平行可得，由正弦定理可得，即，又，所以或，即或，当时，，此时两直线重合，不符合题意，舍去.则是直角三角形.‎ ‎4. B ‎5. B ‎6.C ‎7.C【解析】等比数列的公比，若，则，所以A错误；若，则，所以B错误；若，则时，，时，与同号），所以C一定成立；易知D不成立.‎ ‎8.B【解析】由题意得：，且，解得.，所以：当时，取到最大值.‎ ‎9. A【解析】由线性区域可得，由题意得，表示与两点连线的斜率，由线性规划可得，所以，.‎ ‎10.B ‎11.B ‎12.D 【解析】由得，‎ 所以当时，满足只有一个整数解或当时，满足只有一个整数解.‎ 令，所以，‎ 令，得，所以在单调递增，单调递减，所以，又，‎ ‎，所以存在，使，‎ 所以在，单调递减，在，单调递增，‎ 所以当时，，当时，，又 ‎，‎ 且，所以有且只有一个整数解的解为或，所以或，即或 ‎13. ‎ ‎14. ‎ ‎15. ‎ ‎16. ‎ ‎17. 【解析】（1），在中，由余弦定理知，得，则 ‎.在直角中，.‎ ‎（2）设，则，在直角中，，在中，由正弦定理知.所以，由题意知，所以的取值范围是.‎ ‎18.【解析】（Ⅰ）证明：∵　PD＝PB，且O为BD中点，∴　PO⊥BD.‎ 在菱形ABCD中，∵　∠BCD＝600，AB＝2，∴　OA＝，OB＝1.‎ 又PB＝2，　∴　PO＝.　　‎ ‎∵　PA＝，∴　PA2＝PO2＋OA2，PO⊥OA.‎ ‎∵　 BD∩AO＝O，∴　PO⊥平面ABCD；‎ ‎（Ⅱ）建立如图所示坐标系，则 A(，0，0)，B(0，1，0)，C(－，0，0)，D(0，－1，0)，P(0，0，).‎ z A P B C D O x y M ‎∴　＝(－，1，0)，＝(0，－1，)，＝(－，－1，0)，＝(，-1，0)，‎ 设平面ABP的一个法向量为n1，由得n1＝(1，，1)‎ 设＝λ，则＝＋＝＋λ＝((λ-1)，－(λ+1)，0).‎ 设平面BPM的一个法向量为n2，由得n2＝(λ+1，(λ－1)，λ－1)‎ 由　|cos< n1，n2>|＝ ＝得　5λ2－6λ＋1＝0，∴　λ＝1或λ＝.‎ 即，当点M与点D重合或||＝||时，锐二面角的余弦值为.‎ ‎19.【解析】解：（1）∵语文成绩服从正态分布， ‎ ‎∴语文成绩特别优秀的概率为， ‎ 数学成绩特别优秀的概率为，‎ ‎∴语文特别优秀的同学有人，‎ 数学特别优秀的同学有人．‎ ‎（2）语文数学两科都优秀的有人，单科优秀的有人，‎ 的所有可能取值为，‎ ‎ ‎ ‎∴的分布列为：‎ ‎.‎ ‎（3）2×2列联表：‎ 语文特别优秀 语文不特别优秀 合计 数学特别优秀 ‎6‎ ‎6‎ ‎12‎ 数学不特别优秀 ‎4‎ ‎484‎ ‎488‎ 合计 ‎10‎ ‎490‎ ‎500‎ ‎∴‎ ‎∴有以上的把握认为语文特别优秀的同学，数学也特别优秀．‎ ‎20. 【解析】（Ⅰ）依题意可知，即，由右顶点为，‎ 得，解得，所以的标准方程为.‎ ‎（Ⅱ）依题意可知的方程为，假设存在符合题意的直线，‎ 设直线方程为，，，，,‎ 联立方程组，得，‎ 由韦达定理得，，则，‎ 联立方程组，得，由韦达定理得，，所以，若，则，即，解得，‎ 所以存在符合题意的直线方程为或.‎ ‎21.【解析】（1）‎ 已知 因为，由得或.‎ ① 当时，，单调递增，故无极值；‎ ② 当时，，则 ‎+‎ ‎-‎ ‎+‎ 递增 极大值 递减 极小值 递增 所以：有极大值，极小值 ‎③时，，则 ‎+‎ ‎-‎ ‎+‎ 递增 极大值 递减 极小值 递增 所以：有极大值，极小值 综上所述：时，有极大值，极小值；‎ 时，无极值；‎ 时，有极大值，极小值；‎ ‎（2）令，则，‎ 且 ‎①时，，所以当时，，单调递减，所以，此时，不满足题意；‎ ① 由于与由相同的单调性，由（1）知 a.当时，在上单增，且，所以时，，时，，‎ 所以当时，恒有，满足题意；‎ b.当时，在上单减，所以时，，此时 ‎，不满足题意；‎ c.当时，在递减，所以当时，，此时 ‎，不满足题意；‎ 综上：.‎ ‎22.【解析】（1）曲线的普通方程：，即.‎ 所以的极坐标方程为，即.‎ 曲线的直角坐标方程：，...........5分 ‎（2）依题意，设点、的极坐标分别为.‎ 将代入，得，‎ 将代入，得，‎ 所以，依题意得，点到曲线的距离为.所以. ......10分 ‎23. 【解析】（1）当时，，则，‎ 由解得或，即原不等式的解集为.‎ ‎.......5分 ‎（2），即，又且，‎ 所以且 所以.即.‎ 令，则，‎ 所以时，，‎ 所以，解得，‎ 所以实数的取值范围是. ......10分 ‎