2017-2018学年黑龙江省哈尔滨师范大学青冈实验中学校（师大附中分校）高二4月月考数学（理）试题 Word版

2017-2018学年黑龙江省哈尔滨师范大学青冈实验中学校（师大附中分校）高二4月月考数学（理）试题 Word版

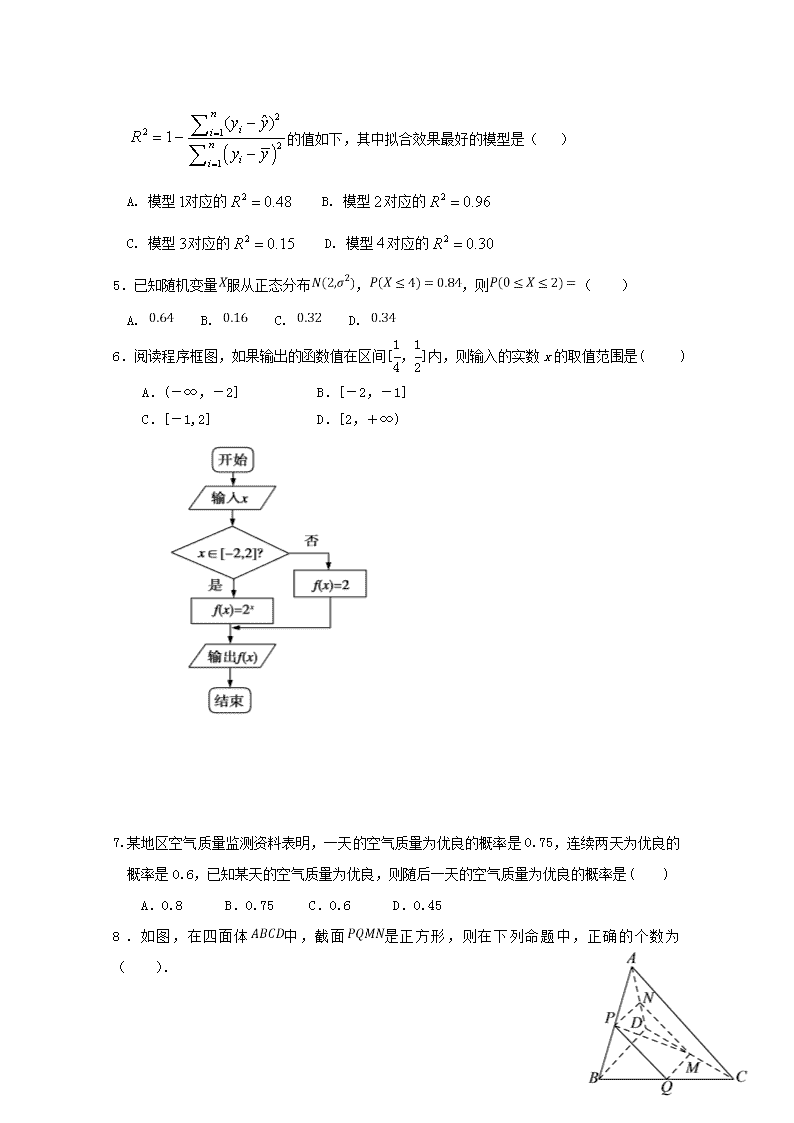
哈师大青冈实验中学2017--2018学年度第二学期4月份考试 高二学年数学（理科）试卷 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试时间120分钟，满分150分。‎ 注意事项：‎ ‎1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上。‎ ‎2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎3．考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。‎ ‎4．保持卡面清洁，不折叠，不破损。‎ 第I卷 选择题 一、选择题：（本大题共12小题，每小题5分，共60分）‎ ‎1．2018年元旦晚会上，某同学从《远走高飞》，《非你莫属》，《两只老虎》，《超越梦想》四首歌中选出两首歌进行表演，则《两只老虎》未选取的概率为( )‎ A. B. C. D. ‎ ‎2．下列随机变量X不是离散型随机变量的是 (　　)‎ A. 某机场候机室中一天的游客数量为X B. 某寻呼台一天内收到的寻呼次数为X C. 某水文站观察到一天中长江的水位为X D. 某立交桥一天经过的车辆数为X ‎3．某企业在甲、乙、丙、丁四个城市分别有150个，120个，190个，140个销售点．为了调查产品的质量，需从这600个销售点中抽取一个容量为100的样本，记这项调查为①；在丙城市有20个特大型销售点，要从中抽取8个调查，记这项调查为②，则完成①，②这两项调查宜采用的抽样方法依次为(　　)‎ A. 分层抽样法、系统抽样法 B. 分层抽样法、简单随机抽样法 C. 系统抽样法、分层抽样法 D. 简单随机抽样法、分层抽样法 ‎4．两个变量与的回归模型中，分别选择了个不同模型，它们对应的 的值如下，其中拟合效果最好的模型是（ ）‎ A. 模型对应的 B. 模型对应的 C. 模型对应的 D. 模型对应的 ‎5．已知随机变量服从正态分布，，则（ ）‎ A. B. C. D. ‎ ‎6．阅读程序框图，如果输出的函数值在区间[，]内，则输入的实数x的取值范围是( )‎ A．(－∞，－2] B．[－2，－1] ‎ C．[－1,2] D．[2，＋∞)‎ ‎7.某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是(　　)‎ A．0.8 B．0.75 C．0.6 D．0.45‎ ‎8．如图，在四面体中，截面是正方形，则在下列命题中，正确的个数为（ ）．‎ ‎（） （） 截面 ‎ ‎（） （）异面直线与所成的角为 A. B. C. D. ‎ ‎9．已知函数是的导函数，则函数的一个单调递减区间是（ ）‎ A. B. C. D. ‎ ‎10．2017年，北京召开“一带一路”国际高峰论坛，组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行互动提问，要求这三个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数为（ ）‎ A. 198 B. 268 C. 306 D. 378‎ ‎11．为直观判断两个分类变量和之间是否有关系，若它们的取值分别为和，通过抽样得到频数表为：‎ 则下列哪两个比值相差越大，可判断两个分类变量之间的关系应该越强（ ）‎ A. 与 B. 与 C. 与 D. 与 ‎12．一个射箭运动员在练习时只记射中环和环的成绩，未击中环或环就以环记．该远动员在练习时击中环的概率为，击中环的概率为，既未击中环也未击中环的概率为（，，），如果已知该运动员一次射箭击中环数的期望为环，则当取最小值 时，的值为（ ）‎ A． B． C． D． ‎ 第II卷 非选择题 二、填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13．的展开式中， 的系数为15，则a=________.(用数字填写答案)‎ ‎14．空气质量指数（，简称）是定量描述空气质量状况的指数，空气质量按照大小分为六级，0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；大于300为严重污染．某环保人士从当地某年的记录数据中，随机抽取10天的数据，用茎叶图记录如下．根据该统计数据，估计此地该年大于100的天数约为__________．（该年为365天）‎ ‎15．“勾股定理”在西方被称为“毕达哥拉斯定理”，三国时期吴国的数学家赵爽创制了一幅“勾股圆 方图”，用数形结合的方法给出了勾股定理的详细证明．如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是__________．‎ ‎16．设曲线y＝ex在点(0，1)处的切线与曲线y ＝ (x＞0)上点P处的切线垂直，则P的坐标为________.‎ 三、解答题：（本大题共6小题，其中17题10分，其余每题12分，共70分）‎ ‎17．加工某种零件需要经过三道工序，设第一、二、三道工序的合格率分别为 ‎，且各道工序互不影响.‎ ‎(1)求该种零件的合格率；‎ ‎(2)从该种零件中任取3件，求恰好取到一件合格品的概率和至少取到一件合格品的概率.‎ ‎18．随着生活水平的提高，人们的休闲方式也发生了变化．某机构随机调查了n个人，其中男性占调查人数的.已知男性中有一半的人的休闲方式是运动，而女性只有的人的休闲方式是运动．‎ ‎(1)完成下列2×2列联表：‎ 运动 非运动 总计 男性 女性 总计 n ‎(2)若在犯错误的概率不超过0.05的前提下，可认为“性别与休闲方式有关”，那么本次被调查的人数至少有多少？‎ ‎(3)根据(2)的结论，本次被调查的人中，至少有多少人的休闲方式是运动？‎ 参考公式：K2＝，其中n＝a＋b＋c＋d.‎ 参考数据：‎ P(K2≥k0)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎19．2014年8月22日是邓小平同志110周年诞辰，为纪念邓小平同志110周年诞辰，促进广安乃至四川旅游业进一步发展，国家旅游局把2014年“5.19”中国旅游日主会场放在四川广安．为迎接旅游日的到来，某旅行社组织了14人参加“四川旅游常识”知识竞赛，每人回答3个问题，答对题目个数及对应人数统计结果见下表：‎ 答对题目个数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 人数 ‎3‎ ‎2‎ ‎5‎ ‎4‎ 根据上表信息解答以下问题：‎ ‎(1)从14人中任选3人，求3人答对题目个数之和为6的概率；‎ ‎ (2)从14人中任选2人，用X 表示这2人答对题目个数之和，求随机变量X的分布列．‎ ‎20．如图，在直三棱柱中，，，是的中点．‎ ‎（1）求证：平面；‎ ‎（2）求二面角的余弦值；‎ ‎（3）试问线段上是否存在点，使异面直线与的夹角为.若存在，确定点位置，若不存在，说明理由． ‎ ‎21．某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上年度的出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 保费 ‎0.85‎ ‎1.25‎ ‎1.5‎ ‎1.75‎ ‎2‎ 设该险种一续保人一年内出险次数与相应概率如下：‎ 一年内出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 概率 ‎0.30‎ ‎0.15‎ ‎0.20‎ ‎0.20‎ ‎0.10‎ ‎0.05‎ ‎（1）求一续保人本年度的保费高于基本保费的概率；‎ ‎（2）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；‎ ‎（3）求续保人本年度的平均保费与基本保费的比值．‎ ‎22．为回馈顾客，某商场拟通过摸球兑奖的方式对1000位顾客进行奖励，规定：每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球，球上所标的面值之和为该顾客所获的奖励额.‎ ‎（1）若袋中所装的4个球中有1个所标的面值为50元，其余3个均为10元，求 ‎ ①顾客所获的奖励额为60元的概率；‎ ‎②顾客所获的奖励额的分布列及数学期望;‎ ‎（2）商场对奖励总额的预算是60000元，并规定袋中的4个球只能由标有面值10元和 ‎50元的两种球组成，或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡，请对袋中的4个球的面值给出一个合适的设计，并说明理由.‎ 高二理数月考答案 BCBBD BACCA AD ‎ 146 　(1，1)‎ ‎17．（1） (这种零件合格) _______________4分 ‎（2）（恰好取到一件合格品）----6分 ‎（至少取到一件合格品）----10分 ‎18．解：(1)依题意，被调查的男性人数为，其中有人的休闲方式是运动；被调查的女性人数为，其中有人的休闲方式是运动，则2×2列联表如下：‎ 运动 非运动 总计 男性 女性 总计 n ‎(4分)‎ ‎(2)由表中数据，得K2＝＝，要使在犯错误的概率不超过0.05的前提下，认为“性别与休闲方式有关”，则K2≥3.841，所以≥3.841，解得n≥138.276.又n∈N*且∈N*，所以n≥140，‎ 即本次被调查的人数至少是140.(9分)‎ ‎(3)由(2)可知：140×＝56，即本次被调查的人中，至少有56人的休闲方式是运动．(12分)‎ ‎19．‎ ‎----4分 ‎(2)依题意可知X的所有可能取值为0,1,2,3,4,5,6.-------5分 则P(X＝0)＝＝＝，P(X＝1)＝＝＝，‎ P(X＝2)＝＝＝，P(X＝3)＝＝＝，‎ P(X＝4)＝＝＝，P(X＝5)＝＝＝，‎ P(X＝6)＝＝＝.------------------------10分 从而X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P ‎--------12分 ‎20．【解析】（1）证明：连结，交于点，连结.‎ 由是直三棱柱，‎ 得 四边形为矩形，为的中点.‎ 又为中点，所以为中位线，‎ 所以，‎ 因为 平面，平面， ‎ 所以平面. ---------4分 ‎（2）解：由是直三棱柱，且，故两两垂直.‎ 如图建立空间直角坐标系. ‎ 则，，，，.‎ 所以，. ‎ 设平面的法向量为，则有，‎ 所以 ， 取，得. ‎ 易知平面的法向量为. ‎ 由二面角是锐角，得.‎ 所以二面角的余弦值为.------------8分 ‎----12分 ‎21．试题解析：（Ⅰ）设表示事件：“一续保人本年度的保费高于基本保费”，则事件发生当且仅当一年内出险次数大于1，故------2分 ‎（Ⅱ）设表示事件：“一续保人本年度的保费比基本保费高出”，则事件发生当且仅当一年内出险次数大于3，故 又，故 因此所求概率为----------7分 ‎ （Ⅲ）记续保人本年度的保费为，则的分布列为 因此续保人本年度的平均保费与基本保费的比值为。--------12分 ‎22．‎ ‎---------5分 ‎(2)根据商场的预算，每个顾客的平均奖励额为60元，所以，先寻找期望为60元的可能方案.‎ 对于面值由10元和50元组成的情况.如果选择的方案，因为60元是面值之和的最大值.所以期望不可能为60元；如果选择的方案，因为60元是面值之和的最小值，所以期望也不可能为60元，因此可能的方案是，记为方案1.‎ 对于面值由20元和40元组成的情况，同理可排除和 的方案，所以可能的方案是，记为方案2--------7分 以下是对两个方案的分析：‎ 对于方案1，即方案，设顾客所获的奖励额为，则的分布列为 ‎20‎ ‎60‎ ‎100‎ 的期望为，‎ 的方差为------9分 对于方案2，即方案，设顾客所获的奖励额为，则的分布列为 ‎20‎ ‎60‎ ‎80‎ 的期望为，‎ 的方差为.------11分 由于两种方案的奖励额的期望都符合要求，但方案2奖励额的方差比方案1小，所以应该选择方案2.--------12分