2019-2020学年河南省天一大联考高二上学期阶段性测试（一）（全国版A卷） 数学（理） （Word版）

2019-2020学年河南省天一大联考高二上学期阶段性测试（一）（全国版A卷） 数学（理） （Word版）

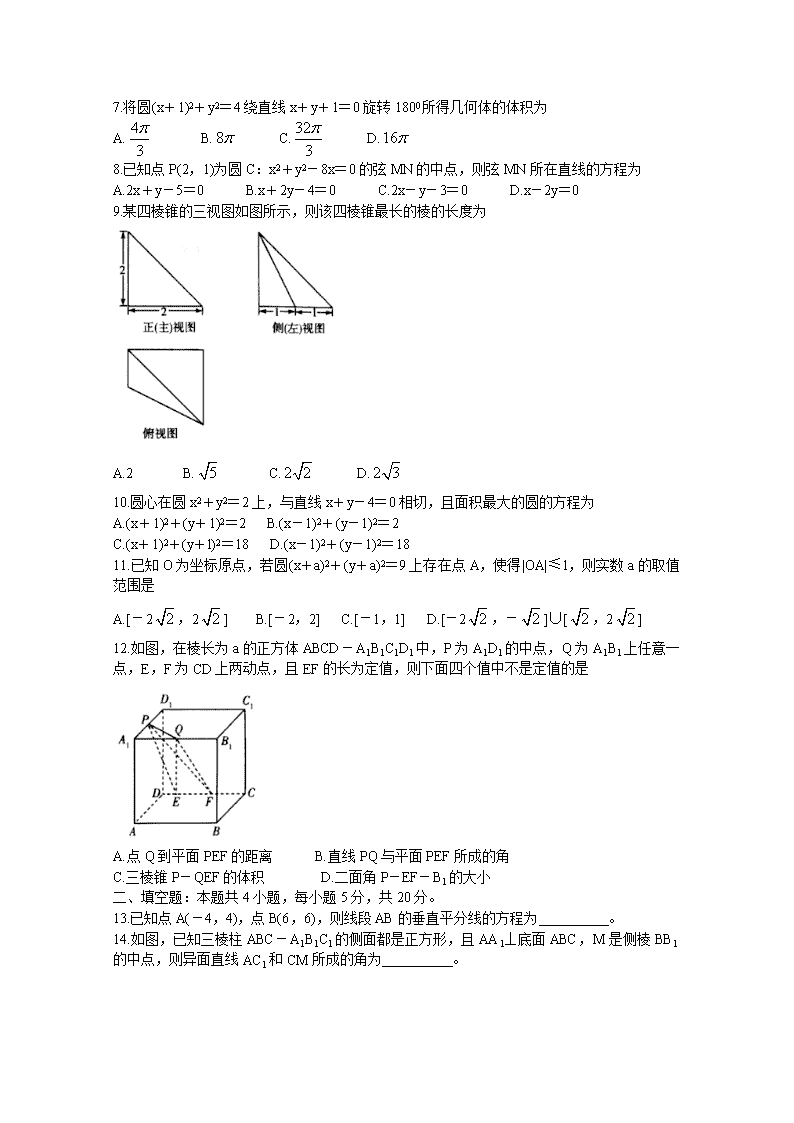
绝密★启用前 试卷类型：全国版A卷 天一大联考 ‎2019－2020学年高二年级阶段性测试(一)‎ 理科数学 考生注意：‎ ‎1.答题前，考生务必将自己的姓名、考生号填写在试卷和答题卡上，并将考生号条形码粘贴在答题卡上的指定位置。‎ ‎2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ ‎3.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.直线：x＋y－＝0的倾斜角为 A.300 B.450 C.600 D.1350‎ ‎2.下列命题中正确的是 A.垂直于同一平面的两个平面平行 B.存在两条异面直线同时平行于同一个平面 C.若一个平面中有无数条直线与另一个平面平行，则这两个平面平行 D.三点确定一个平面 ‎3.已知两条直线l1：(a－1)x＋2y＋1＝0，l2：x＋ay＋l＝0平行，则a＝‎ A.－1 B.2 C.0或－2 D.－1或2‎ ‎4.在空间直角坐标系Oxyz中，点(1，－2，4)关于y轴对称的点为 A.(－1，－2，－4) B.(－1，－2，4) C.(1，2，－4) D.(1，2，4)‎ ‎5.如图，球O内切于圆柱O1O2，记圆柱O1O2的侧面积为S1，球O的表面积为S2，则 A. B.S1＝S2 C.S1＝2S2 D. ‎ ‎6.若直线l：ax－y＋a＝0被圆C：x2＋(y－1)2＝4所截得的弦长为2，则a＝‎ A.3 B.2 C.1 D.0‎ ‎7.将圆(x＋1)2＋y2＝4绕直线x＋y＋1＝0旋转1800所得几何体的体积为 A. B. C. D. ‎ ‎8.已知点P(2，1)为圆C：x2＋y2－8x＝0的弦MN的中点，则弦MN所在直线的方程为 A.2x＋y－5＝0 B.x＋2y－4＝0 C.2x－y－3＝0 D.x－2y＝0‎ ‎9.某四棱锥的三视图如图所示，则该四棱锥最长的棱的长度为 A.2 B. C. D. ‎ ‎10.圆心在圆x2＋y2＝2上，与直线x＋y－4＝0相切，且面积最大的圆的方程为 A.(x＋1)2＋(y＋1)2＝2 B.(x－1)2＋(y－1)2＝2 ‎ C.(x＋1)2＋(y＋l)2＝18 D.(x－1)2＋(y－1)2＝18‎ ‎11.已知O为坐标原点，若圆(x＋a)2＋(y＋a)2＝9上存在点A，使得|OA|≤1，则实数a的取值范围是 A.[－2，2] B.[－2，2] C.[－1，1] D.[－2，－]∪[，2]‎ ‎12.如图，在棱长为a的正方体ABCD－A1B1C1D1中，P为A1D1的中点，Q为A1B1上任意一点，E，F为CD上两动点，且EF的长为定值，则下面四个值中不是定值的是 A.点Q到平面PEF的距离 B.直线PQ与平面PEF所成的角 C.三棱锥P－QEF的体积 D.二面角P－EF－B1的大小 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.已知点A(－4，4)，点B(6，6)，则线段AB的垂直平分线的方程为 。‎ ‎14.如图，已知三棱柱ABC－A1B1C1的侧面都是正方形，且AA1⊥底面ABC，M是侧棱BB1的中点，则异面直线AC1和CM所成的角为 。‎ ‎15.若A(－3，y0)是直线l：x－y－a＝0(a<0)上的点，直线l与圆C：x2＋y2－2x＋4y－5＝0相交于M，N两点。若△MCN为等边三角形，过点A作圆C的切线，切点为P，则|AP|＝ 。‎ ‎16.已知矩形ABCD中，AB＝2，BC＝3，点E，F分别在边AD，BC上，且，。现沿EF将图形折起，形成二面角A－EF－D为600的一个空间几何体，则该空间几何体的外接球的表面积为 。‎ 三、解答题：共70分。解答应写出文字说明，证明过程或演算步骤。‎ ‎17.(10分)‎ 已知直线l过点P(2，－1)。‎ ‎(I)若原点O到直线l的距离为2，求直线l的方程；‎ ‎(II)当原点O到直线l的距离最大时，求直线l的方程。‎ ‎18.(12分)‎ 如图，在三棱锥P－ABC中，PA＝PB＝PC＝AC＝BC＝，AB＝2，D是PB的中点。‎ ‎(I)求证：AB⊥PC；‎ ‎(II)求点D到平面PAC的距离。‎ ‎19.(12分)‎ 已知点A(2，a)，圆C：(x－1)2＋y2＝5。‎ ‎(I)若过点A只能作一条圆C的切线，求实数a的值及切线方程；‎ ‎(II)设直线l过点A但不过原点，且在两坐标轴上的截距相等，若直线l被圆C截得的弦长为2，求实数a的值。‎ ‎20(12分)‎ 如图，在四棱锥P－ABCD中，四边形ABCD是平行四边形，且∠BAD＝600，平面PAB⊥平面，ABCD，E、F分别为AD、PB的中点。‎ ‎(I)求证：EF//平面PCD；‎ ‎(II)若PA＝PB＝AD＝1，∠APB＝900，求三棱锥P－CEF的体积。‎ ‎21.(12分)‎ 如图，在三棱柱ABC－A1B1C1中，各棱长相等，侧棱垂直于底面ABC，E，F分别是BC，A1C1的中点。‎ ‎(I)求证：平面AEF⊥平面B1BCC1；‎ ‎(II)求证：C1E//平面ABF；‎ ‎(III)求AC1与平面BB1C1C所成角的正弦值。‎ ‎22.(12分)‎ 如图，在平面直角坐标系xOy，过点P(0，1)且互相垂直的两条直线分别与圆O：x2＋y2＝4交于点A，B，与圆M：(x－2)2＋(y－1)2＝1交于点C，D。‎ ‎(I)若直线AB的斜率为3，求△ABM的面积；‎ ‎(II)若，求CD的长；‎ ‎(III)若CD的中点为E，求△ABE面积的取值范围。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎