高中数学第五章 1_2 复数的有关概念 课件

高中数学第五章 1_2 复数的有关概念 课件

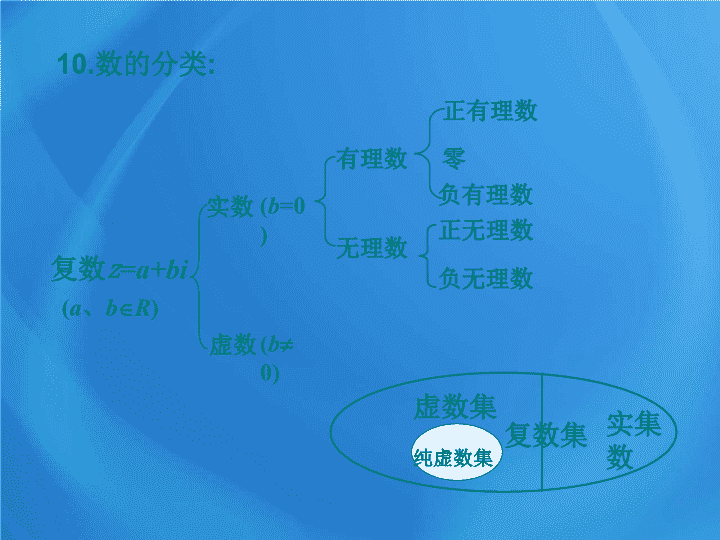
第五章 数系的扩充与复数的引入 1.2 复数的有关概念 知识回顾 : 1. 复数的概念 : 形如 a+bi(a,b∈R) 的数叫做复数 . 2. 虚数单位 : i 3. 全体复数组成的的集合叫 : 复数集 , 用 C 表示 . 4. 复数的代数形式 : Z=a+bi 5. 复数的实部与虚部分别是 : a,b 6.a + bi 是实数 b =0 7. a + bi 是 虚数 b ≠0 8.a + bi 为纯虚数 a =0 且 b ≠0 9. 两个复数能比较大小吗 ? 不能 复数 z = a+bi ( a 、 b  R ) 实数 ( b =0) 有理数 无理数 正有理数 负有理数 零 虚数 ( b  0) 10. 数的分类 : 复数集 实集数 虚数集 纯虚数集 正无理数 负无理数 如果两个复数的 实部 和 虚部 分别相等，那么我们就说这两个 复数相等 ． 特别地， 例 1 已知 ，其中 求 解：根据复数相等的定义，得方程组 解得 在几何上，我们用什么来表示实 数 ? 想一想？ 实数的几何意义 类比 实数的表示，可以用什么来表示复数？ 实数可以用 数轴 上的点来表示。 实数 数轴 上的点 ( 形 ) ( 数 ) 一一对应 复数 z=a+bi 有序实数对 (a,b) 直角坐标系中的点 Z(a,b) x y o b a Z(a,b) 建立了平面直角坐标系来表示复数的平面 x 轴 ------ 实轴 y 轴 ------ 虚轴 （数） （形） ------ 复数平面 ( 简称 复平面 ) 一一对应 z=a+bi 复数的几何意义（一） 注 : 实轴上的点表示实数 , 虚轴上的点 ( 除原点 ) 都表示纯虚数 ) (A) 在复平面内，对应于实数的点都在实轴上； (B) 在复平面内，对应于纯虚数的点都在虚轴上； (C) 在复平面内，实轴上的点所对应的复数都是实数； (D) 在复平面内，虚轴上的点所对应的复数都是纯虚数。 例 2. (1) 下列命题中的假命题是（ ） D 例 3 : 已知复数 z=(m 2 +m-6)+(m 2 +m-2)i 在复平面内所对应的点位于第二象限，求实数 m 的取值范围。 一种重要的数学思想： 数形结合思想 练习 1 ： 已知复数 z=(m 2 +m-6)+(m 2 +m-2)i 在复平面内所对应的点在 直线 x-2y+4=0 上，求实数 m 的值。 解：∵ 复数 z=(m 2 +m-6)+(m 2 +m-2)i 在复平面内所对应的点是（ m 2 +m-6 ， m 2 +m-2 ）， ∴ (m 2 +m-6)-2(m 2 +m-2)+4=0 ， ∴ m=1 或 m=-2 。 复数 z=a+bi 直角坐标系中的点 Z(a,b) 一一对应 平面向量 一一对应 一一对应 复数的几何意义（二） x y o b a Z(a,b) z=a+bi 注意 : 相等的向量表示同一个复数 . x O z = a + b i y 复数的绝对值 ( 复数的模 ) 的 几何意义 : Z ( a , b ) 对应平面向量 的模 | | ， 即 复数 z=a+bi 在复平面上对应的点 Z( a , b ) 到原点的距离。 | z | = 例 4: 求下列复数的模： (1)z 1 =-5i (2)z 2 =-3+4i (3)z 3 =5-5i (4)z 4 =1+mi(m∈R) (5)z 5 =4a-3ai(a<0) ( 5 ) ( 5 ) ( － 5a ) 小结 : 1. 复数 z=a+bi 直角坐标系中的点 Z(a,b) 一一对应 2. 建立了平面直角坐标系来表示复数的平面 x 轴 ------ 实轴 y 轴 ------ 虚轴 ------ 复数平面 ( 简称 复平面 ) 3. 复数 z=a+bi 平面向量 一一对应 | z | = 4. 复数的模 :