2017-2018学年内蒙古杭锦后旗奋斗中学高二下学期第一次月考数学（文）试题 Word版

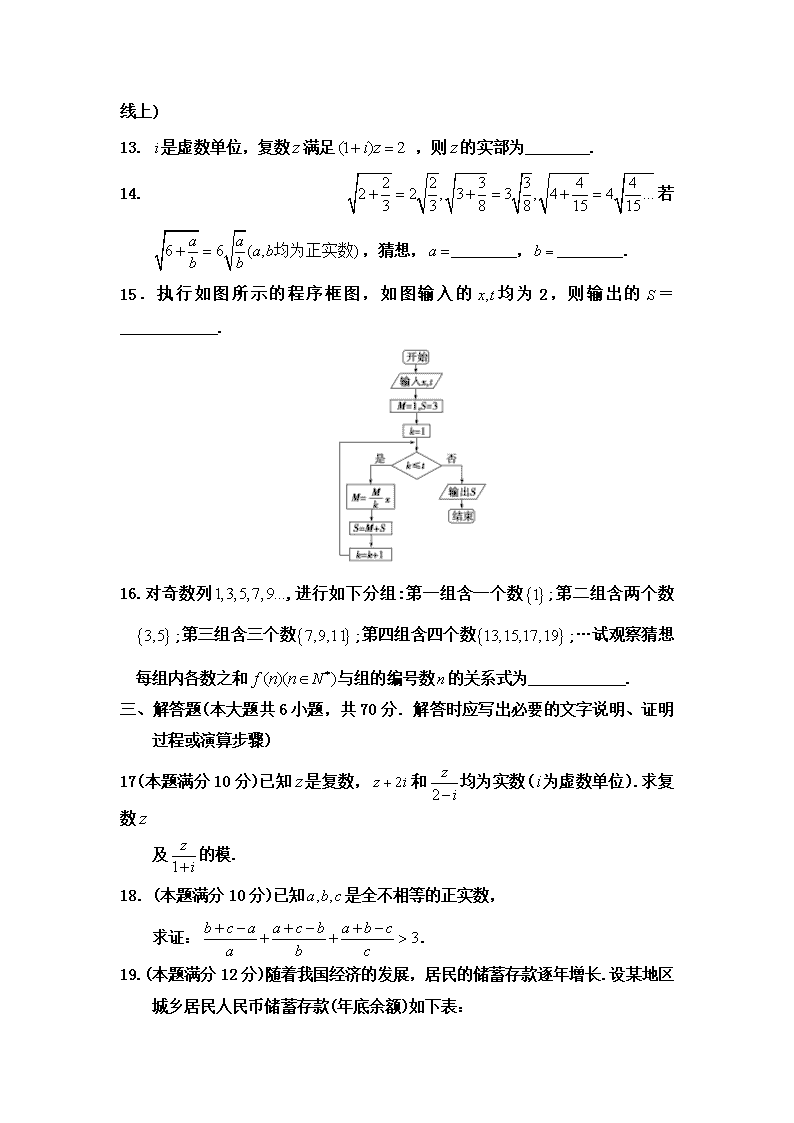
2017-2018学年内蒙古杭锦后旗奋斗中学高二下学期第一次月考数学（文）试题 Word版

奋斗中学2017—2018年第二学期第一次月考试题 高二数学（文）‎ ‎(时间：120分钟　满分：150分)‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1. 为虚数单位，=(　　)‎ ‎ A.　　　　B.-　　　　 C.1　　　 　D.-1‎ ‎2．若，，则的大小关系为(　　)‎ A． B． C． D．由的取值确定 ‎3.下面是关于复数的四个命题：，， 的共轭复数为，的虚部为1，其中真命题为(　　)‎ A. B. C. D. ‎ ‎4．某考察团对全国10大城市进行职工人均工资水平(千元)与居民人均消费水平(千元)统计调查发现，与具有相关关系，回归方程为.若某城市居民人均消费水平为7.675(千元)，估计该城市人均消费额占人均工资收入的百分比约为(　　)‎ A．83% B．72% C．67% D．66%‎ ‎5.某成品的组装工序流程图如图所示，箭头上的数字表示组装过程中所需要的时间(小时)，不同车间可同时工作，同一车间不能同时做两种或两种以上的工作，则组装该产品所需要的最短时间是(　　)‎ A.11小时 B.13小时 C.15小时 D.17小时 ‎6．在复平面内，复数, 对应的点分别为.若为线段 的中点，则点对应的复数是（ ） ‎ ‎ A. B. C. D. ‎ ‎7．根据如图所示的框图，对大于2的整数N，输出的数列的通项公式是(　　)‎ A． B． C． D．‎ ‎8．为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下：‎ 父亲身高 ‎174‎ ‎176‎ ‎176‎ ‎176‎ ‎178‎ 儿子身高 ‎175‎ ‎175‎ ‎176‎ ‎177‎ ‎177‎ 则对的线性回归方程为(　　)‎ A． B． C． D．‎ ‎9．观察下列各式：，，，，，…，则(　　)‎ A．28 B．76 C．123 D．199‎ ‎10.经统计，某地的财政收入与支出满足的线性回归模型是(单位：亿元).其中为随机误差，如果今年该地财政收入为10亿元，则今年支出预计不超出(　　)‎ A.10亿元 B.11亿元 C. 11.5亿元 D.12亿元 ‎11.如果对象和对象都具有相同的属性等，此外已知对象还有一个属性，而对象还有一个未知的属性，由此类比推理，可以得出下列哪个结论可能成立(　　)‎ A. 就是 B.就是 C.就是 D.就是 ‎12.观察下列各式：的不同整数解 的个数为4，的不同整数解 的个数为8，的不同整数解 的个数为12，…，则的不同整数解 的个数为(　　)‎ A.76 B.80 C.86 D.92‎ 二、填空题(本大题共4小题，每小题5分，共20分.请把正确答案填在题中横线上)‎ ‎13. 是虚数单位，复数满足 ，则的实部为________.‎ ‎14. 若，猜想，________，________．‎ ‎15．执行如图所示的程序框图，如图输入的均为2，则输出的＝____________.‎ ‎16.对奇数列,进行如下分组:第一组含一个数;第二组含两个数;第三组含三个数;第四组含四个数;…试观察猜想每组内各数之和与组的编号数的关系式为____________.‎ 三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17(本题满分10分)已知是复数，和均为实数(为虚数单位).求复数 及的模.‎ 18． ‎(本题满分10分)已知是全不相等的正实数，‎ 求证：. ‎ ‎19.( 本题满分12分)随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 时间代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款(千亿元)‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎(1)求关于的回归方程 ‎(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.‎ 附：回归方程中，‎ ‎20．（本题满分12分）已知的三边长分别为，且其中任意两边长均不相等，若成等差数列．‎ ‎(1)比较与的大小，并证明你的结论；‎ ‎(2)求证：角不可能是钝角．‎ ‎21.( 本题满分14分)某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的质量(单位：克)，质量值落在(495，510]的产品为合格品，否则为不合格品.如表是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图.‎ 产品质量/克 频数 ‎(490，495]‎ ‎6‎ ‎ (495，500]‎ ‎8‎ ‎(500，505]‎ ‎14‎ ‎(505，510]‎ ‎8‎ ‎(510，515]‎ ‎4‎ 甲流水线样本频数分布表 ‎(1)根据上表数据作出甲流水线样本的频率分布直方图.‎ ‎(2)若以频率作为概率，试估计从乙流水线任取1件产品，该产品恰好是合格品的概率.‎ ‎(3)由以上统计数据完成下面2×2列联表，能否在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关？‎ 甲流水线 乙流水线 总计 合格品 不合格品 总计 附表：‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7. 879‎ ‎10.828‎ ‎（参考公式：）‎ 22、 ‎（本题满分12分）‎ ‎（1）已知，证明：；‎ ‎（2）已知 ，求证：‎ 答案：‎ ‎ ‎ 13. ‎1；14. 6,35；15. 7；16. ‎ ‎17. 解：‎ ‎18.证明：全不相等，全不相等，‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎19.解：（1）‎ ‎（2）当时，（千元）‎ ‎20（1）证明：由题知 ‎，则 （2） 证明：，，‎ 角不可能是钝角．‎ ‎21（1）根据所给的每一组的频数和样本容量做出每一组的频率，在平面直角坐标系中做出频率分步直方图， 甲流水线样本的频率分布直方图如下： ‎ ‎（2）由图1知，乙样本中合格品数为（0.06+0.09+0.03）×5×40=36， 故合格品的频率为36/40=0.9据此可估计从乙流水线上任取一件产品该产品为合 格品的概率P=0.9，‎ ‎（3）‎ 甲流水线 乙流水线 总计 合格品 ‎30‎ ‎36‎ ‎66‎ 不合格品 ‎10‎ ‎4‎ ‎14‎ 总计 ‎40‎ ‎40‎ ‎80‎ 能在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关.‎ ‎22.解：略