数学卷·2018届河北省保定市高碑店一中高二上学期第一次月考数学试卷（理科） （解析版）

数学卷·2018届河北省保定市高碑店一中高二上学期第一次月考数学试卷（理科） （解析版）

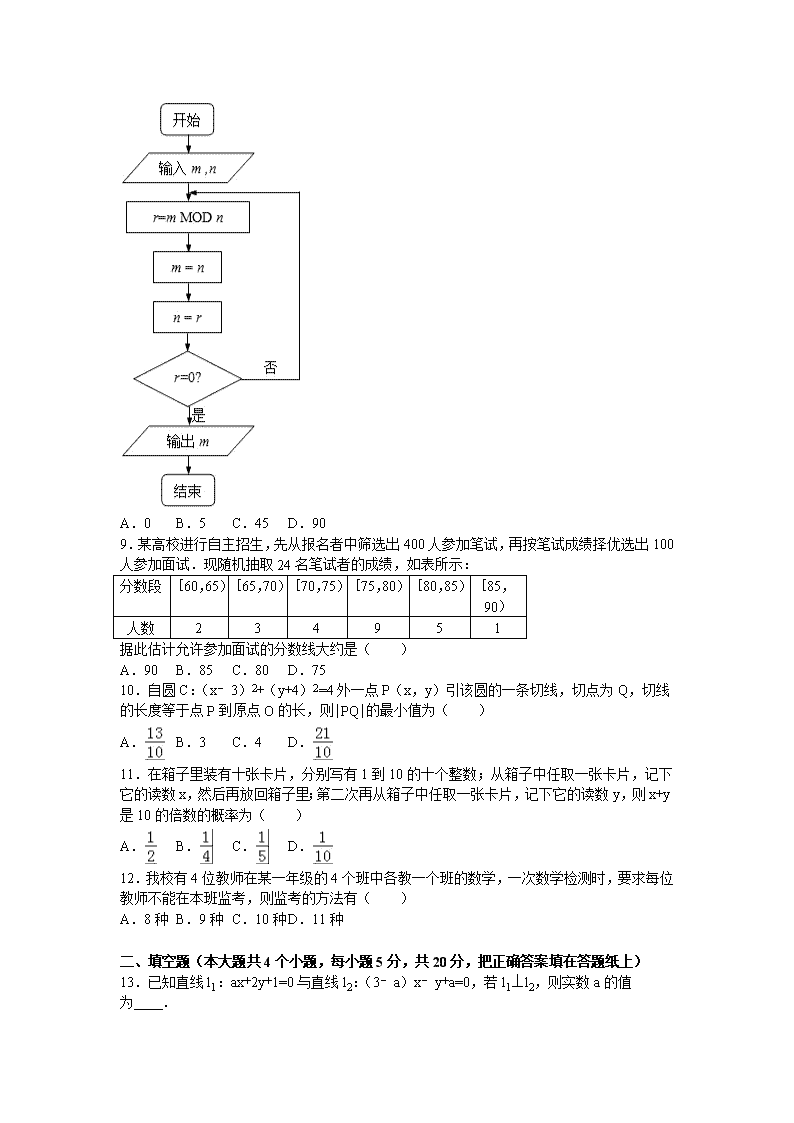
‎2016-2017学年河北省保定市高碑店一中高二（上）第一次月考数学试卷（理科）‎ ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．对于任意实数a，b，c，d，以下四个命题中 ‎①ac2＞bc2，则a＞b； ‎ ‎②若a＞b，c＞d，则a+c＞b+d；‎ ‎③若a＞b，c＞d，则ac＞bd； ‎ ‎④a＞b，则＞．‎ 其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎2．若不等式ax2+2ax﹣4＜2x2+4x对任意实数x均成立，则实数a的取值范围是（　　）‎ A．（﹣2，2） B．（﹣2，2] C．（﹣∞，﹣2）∪[2，∞） D．（∞，2]‎ ‎3．直线l与两直线y=1和x﹣y﹣7=0分别交于A，B两点，若线段AB的中点为M（1，﹣1），则直线l的斜率为（　　）‎ A． B． C． D．‎ ‎4．若x，y满足，则z=y﹣2|x|的最大值为（　　）‎ A．﹣8 B．﹣4 C．1 D．2‎ ‎5．直线ax﹣y+2a=0与圆x2+y2=9的位置关系是（　　）‎ A．相离 B．相交 C．相切 D．不确定 ‎6．圆x2+y2=50与圆x2+y2﹣12x﹣6y+40=0的公共弦长为（　　）‎ A． B． C．2 D．2‎ ‎7．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9．抽到的32人中，编号落入区间[1，450]的人做问卷A，编号落入区间[451，750]的人做问卷B，其余的人做问卷C．则抽到的人中，做问卷B的人数为（　　）‎ A．7 B．9 C．10 D．15‎ ‎8．如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“m MOD n”表示m除以n的余数），若输入的m，n分别为495，135，则输出的m=（　　）‎ A．0 B．5 C．45 D．90‎ ‎9．某高校进行自主招生，先从报名者中筛选出400人参加笔试，再按笔试成绩择优选出100人参加面试．现随机抽取24名笔试者的成绩，如表所示：‎ 分数段 ‎[60，65）‎ ‎[65，70）‎ ‎[70，75）‎ ‎[75，80）‎ ‎[80，85）‎ ‎[85，90）‎ 人数 ‎2‎ ‎3‎ ‎4‎ ‎9‎ ‎5‎ ‎1‎ 据此估计允许参加面试的分数线大约是（　　）‎ A．90 B．85 C．80 D．75‎ ‎10．自圆C：（x﹣3）2+（y+4）2=4外一点P（x，y）引该圆的一条切线，切点为Q，切线的长度等于点P到原点O的长，则|PQ|的最小值为（　　）‎ A． B．3 C．4 D．‎ ‎11．在箱子里装有十张卡片，分别写有1到10的十个整数；从箱子中任取一张卡片，记下它的读数x，然后再放回箱子里；第二次再从箱子中任取一张卡片，记下它的读数y，则x+y是10的倍数的概率为（　　）‎ A． B． C． D．‎ ‎12．我校有4位教师在某一年级的4个班中各教一个班的数学，一次数学检测时，要求每位教师不能在本班监考，则监考的方法有（　　）‎ A．8种 B．9种 C．10种 D．11种 ‎　‎ 二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在答题纸上）‎ ‎13．已知直线l1：ax+2y+1=0与直线l2：（3﹣a）x﹣y+a=0，若l1⊥l2，则实数a的值为　　．‎ ‎14．如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆．在扇形OAB内随机取一点，则此点取自阴影部分的概率是　　．‎ ‎15．正实数x，y满足： +=1，则x2+y2﹣10xy的最小值为　　．‎ ‎16．在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}．‎ ‎（1）求实数a，b的值；‎ ‎（2）解关于x的不等式：＞0（c为常数）．‎ ‎18．彭山二中决定在新校区附近修建教师宿舍，学校行政办公室用100万元从政府购得一块廉价土地，该土地可以建造每层1000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高20元．已知建筑第5层楼房时，每平方米建筑费用为800元．‎ ‎（1）若建筑第x层楼时，该楼房综合费用为y万元（综合费用是建筑费用与购地费用之和），写出y=f（x）的表达式．‎ ‎（2）为了使该楼房每平方米的平均综合费用最低，学校应把楼层建成几层？此时平均综合费用为每平方米多少元？‎ ‎19．过原点且斜率为的直线l1与直线l2：2x+3y﹣1=0交于A点，求过点A且圆心在直线y=﹣2x上，并与直线x+y﹣1=0相切的圆的方程．‎ ‎20．已知直线x﹣y+1=0与圆C：x2+y2﹣4x﹣2y+m=0交于A，B两点；‎ ‎（1）求线段AB的垂直平分线的方程；‎ ‎（2）若|AB|=2，求m的值；‎ ‎（3）在（2）的条件下，求过点P（4，4）的圆C的切线方程．‎ ‎21．为了比较两种治疗失眠症的药（分别成为A药，B药）的疗效，随机地选取20位患者服用A药，20位患者服用B药，这40位患者服用一段时间后，记录他们日平均增加的睡眠时间（单位：h）实验的观测结果如下：‎ 服用A药的20位患者日平均增加的睡眠时间：‎ ‎0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5‎ ‎2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4‎ 服用B药的20位患者日平均增加的睡眠时间：‎ ‎3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4‎ ‎1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5‎ ‎（Ⅰ）分别计算两种药的平均数，从计算结果看，哪种药的疗效更好？‎ ‎（Ⅱ）根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？‎ ‎22．从某学校高三年级共800名男生中随机抽取50人测量身高．据测量，被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…；第八组[190，195]．如图是按上述分组方法得到的频率分布直方图的一部分．已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．‎ ‎（1）估计这所学校高三年级全体男生身高在180cm以上（含180cm）的人数及平均身高；‎ ‎（2）求第六组、第七组的频率并补充完整频率分布直方图；‎ ‎（3）若从身高属于第六组和第八组的所有男生中随机抽取两人，记他们的身高分别为x、y，求满足“|x﹣y|≤5”的事件的概率．‎ ‎　‎ ‎2016-2017学年河北省保定市高碑店一中高二（上）第一次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．对于任意实数a，b，c，d，以下四个命题中 ‎①ac2＞bc2，则a＞b； ‎ ‎②若a＞b，c＞d，则a+c＞b+d；‎ ‎③若a＞b，c＞d，则ac＞bd； ‎ ‎④a＞b，则＞．‎ 其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】不等式的基本性质．‎ ‎【分析】由不等式的性质，逐个选项验证可得．‎ ‎【解答】解：选项①ac2＞bc2，则a＞b正确，由不等式的性质可得； ‎ 选项②若a＞b，c＞d，则a+c＞b+d正确，由不等式的可加性可得；‎ 选项③若a＞b，c＞d，则ac＞bd错误，需满足abcd均为正数才可以； ‎ 选项④a＞b，则＞错误，比如﹣1＞﹣2，但＜．‎ 故选：B ‎　‎ ‎2．若不等式ax2+2ax﹣4＜2x2+4x对任意实数x均成立，则实数a的取值范围是（　　）‎ A．（﹣2，2） B．（﹣2，2] C．（﹣∞，﹣2）∪[2，∞） D．（∞，2]‎ ‎【考点】函数恒成立问题．‎ ‎【分析】将原不等式整理成关于x的二次不等式，结合二次函数的图象与性质解决即可，注意对二次项系数分类讨论 ‎【解答】解：不等式ax2+2ax﹣4＜2x2+4x，可化为（a﹣2）x2+2（a﹣2）x﹣4＜0，‎ 当a﹣2=0，即a=2时，恒成立，合题意．‎ 当a﹣2≠0时，要使不等式恒成立，需，解得﹣2＜a＜2．‎ 所以a的取值范围为（﹣2，2]．‎ 故选B．‎ ‎　‎ ‎3．直线l与两直线y=1和x﹣y﹣7=0分别交于A，B两点，若线段AB的中点为M（1，﹣1），则直线l的斜率为（　　）‎ A． B． C． D．‎ ‎【考点】中点坐标公式．‎ ‎【分析】设出直线l的斜率为k，又直线l过M点，写出直线l的方程，然后分别联立直线l与已知的两方程，分别表示出A和B的坐标，根据中点坐标公式表示出M的横坐标，让表示的横坐标等于1列出关于k的方程，求出方程的解即可得到k的值即为直线的斜率．‎ ‎【解答】解：设直线l的斜率为k，又直线l过M（1，﹣1），则直线l的方程为y+1=k（x﹣1），‎ 联立直线l与y=1，得到，解得x=，所以A（，1）；‎ 联立直线l与x﹣y﹣7=0，得到，解得x=，y=，所以B（，），‎ 又线段AB的中点M（1，﹣1），所以+=2，解得k=﹣．‎ 故选D．‎ ‎　‎ ‎4．若x，y满足，则z=y﹣2|x|的最大值为（　　）‎ A．﹣8 B．﹣4 C．1 D．2‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，分类化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 当x≥0时，可行域为四边形OACD及其内部区域，A点是目标函数取得最大值的点；‎ 当x≤0时，可行域为三角形OAB及其内部区域，A点是目标函数取得最大值的点．‎ ‎∴z=y﹣2|x|的最大值为2．‎ 故选：D．‎ ‎　‎ ‎5．直线ax﹣y+2a=0与圆x2+y2=9的位置关系是（　　）‎ A．相离 B．相交 C．相切 D．不确定 ‎【考点】直线与圆的位置关系．‎ ‎【分析】求出直线恒过的定点，判断定点与圆的位置关系．‎ ‎【解答】解：直线ax﹣y+2a=0恒过定点（﹣2，0），而（﹣2，0）满足22+02＜9，所以直线与圆相交．‎ 故选B．‎ ‎　‎ ‎6．圆x2+y2=50与圆x2+y2﹣12x﹣6y+40=0的公共弦长为（　　）‎ A． B． C．2 D．2‎ ‎【考点】圆与圆的位置关系及其判定．‎ ‎【分析】利用圆系方程直接求出相交弦所在直线方程，通过半弦长，半径，弦心距的直角三角形，求出半弦长，即可得到公共弦长．‎ ‎【解答】解：x2+y2=50，①；x2+y2﹣12x﹣6y+40=0②；‎ ‎②﹣①得：2x+y﹣15=0为公共弦所在直线的方程，‎ 原点到相交弦直线的距离为：，弦长的一半为，公共弦长为：‎ 故选C．‎ ‎　‎ ‎7．采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9．抽到的32人中，编号落入区间[1，450]的人做问卷A，编号落入区间[451，750]的人做问卷B，其余的人做问卷C．则抽到的人中，做问卷B的人数为（　　）‎ A．7 B．9 C．10 D．15‎ ‎【考点】系统抽样方法．‎ ‎【分析】由题意可得抽到的号码构成以9为首项、以30为公差的等差数列，求得此等差数列的通项公式为an=9+（n﹣1）30=30n﹣21，由451≤30n﹣21≤750 求得正整数n的个数．‎ ‎【解答】解：960÷32=30，故由题意可得抽到的号码构成以9为首项、以30为公差的等差数列，且此等差数列的通项公式为an=9+（n﹣1）30=30n﹣21．‎ 由 451≤30n﹣21≤750 解得 15.7≤n≤25.7．‎ 再由n为正整数可得 16≤n≤25，且 n∈z，故做问卷B的人数为10，‎ 故选：C．‎ ‎　‎ ‎8．如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“m MOD n”表示m除以n的余数），若输入的m，n分别为495，135，则输出的m=（　　）‎ A．0 B．5 C．45 D．90‎ ‎【考点】程序框图．‎ ‎【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量m的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．‎ ‎【解答】解：第一次执行循环体，r=90，m=135，n=90，不满足退出循环的条件；‎ 第二次执行循环体，r=0，m=45，n=0，满足退出循环的条件；‎ 故输出的m值为45，‎ 故选：C ‎　‎ ‎9．某高校进行自主招生，先从报名者中筛选出400人参加笔试，再按笔试成绩择优选出100人参加面试．现随机抽取24名笔试者的成绩，如表所示：‎ 分数段 ‎[60，65）‎ ‎[65，70）‎ ‎[70，75）‎ ‎[75，80）‎ ‎[80，85）‎ ‎[85，90）‎ 人数 ‎2‎ ‎3‎ ‎4‎ ‎9‎ ‎5‎ ‎1‎ 据此估计允许参加面试的分数线大约是（　　）‎ A．90 B．85 C．80 D．75‎ ‎【考点】频率分布表．‎ ‎【分析】根据题意，求出参加面试的频率，再计算对应频率的分数段，即可得出分数线大约是多少．‎ ‎【解答】解：参加面试的频率为=0.25，‎ 样本中[80，90）的频率为=0.25，‎ 由样本估计总体知，分数线大约为80分．‎ 故选：C．‎ ‎　‎ ‎10．自圆C：（x﹣3）2+（y+4）2=4外一点P（x，y）引该圆的一条切线，切点为Q，切线的长度等于点P到原点O的长，则|PQ|的最小值为（　　）‎ A． B．3 C．4 D．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】由题意画出图象，根据条件和圆的切线性质列出方程化简，求出点P的轨迹方程，结合条件和两点之间、点到直线的距离公式求出|PQ|的最小值．‎ ‎【解答】解：由题意得，圆心C（3，﹣4），半径r=2，如图：‎ 因为|PQ|=|PO|，且PQ⊥CQ，所以|PO|2+r2=|PC|2，‎ 所以x2+y2+4=（x﹣3）2+（y+4）2，‎ 即6x+8y﹣21=0，所以点P在直线6x+8y﹣21=0上，‎ 要使|PQ|最小，只要|PO|最小即可，‎ 当直线PO垂直于直线6x+8y﹣21=0时，|PQ|最小，‎ 此时|PQ|最小值是=，‎ 故选：D．‎ ‎　‎ ‎11．在箱子里装有十张卡片，分别写有1到10的十个整数；从箱子中任取一张卡片，记下它的读数x，然后再放回箱子里；第二次再从箱子中任取一张卡片，记下它的读数y，则x+y是10的倍数的概率为（　　）‎ A． B． C． D．‎ ‎【考点】相互独立事件的概率乘法公式．‎ ‎【分析】所有的读数（x，y）共有10×10=100个，其中满足x+y是10的倍数的用列举法求得共计10个，从而求得x+y是10的倍数的概率．‎ ‎【解答】解：所有的读数（x，y）共有10×10=100个，其中满足x+y是10的倍数的有（1，9）、（2，8）、（3，7）、（4，6）、（5，5），‎ ‎（9，1）、（8，2）、（7，3）、（6，4）、（10，10），共计10个，‎ 故x+y是10的倍数的概率为=，‎ 故选：D．‎ ‎　‎ ‎12．我校有4位教师在某一年级的4个班中各教一个班的数学，一次数学检测时，要求每位教师不能在本班监考，则监考的方法有（　　）‎ A．8种 B．9种 C．10种 D．11种 ‎【考点】排列、组合及简单计数问题．‎ ‎【分析】首先分析可得当教师监考不受限制时，安排监考的方法有24种，再计算其中有人在本班监考的情况数目，分“有1人在本班监考”、“有2人在本班监考”、“有3人在本班监考”三种情况讨论，易得不符合题意的安排方法数目，进而由事件间的关系可得答案．‎ ‎【解答】解：当教师监考不受限制时，安排监考的方法有4×3×2×1=24种，‎ 其中有1人在本班监考的有C41•2=8种，‎ 有2人在本班监考的有C42=6种，‎ ‎4人全在本班监考的有1种，‎ 则不符合题意的安排方法有8+6+1=15种；‎ 故符合题意的监考方法有24﹣15=9种；‎ 故选B．‎ ‎　‎ 二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在答题纸上）‎ ‎13．已知直线l1：ax+2y+1=0与直线l2：（3﹣a）x﹣y+a=0，若l1⊥l2，则实数a的值为　1或2　．‎ ‎【考点】直线的一般式方程与直线的垂直关系．‎ ‎【分析】利用平面中的直线垂直的条件A1A2+B1B2=0，求出a的值．‎ ‎【解答】解：∵l1：ax+2y+1=0，‎ l2：（3﹣a）x﹣y+a=0，且l1⊥l2，‎ ‎∴a（3﹣a）+2×（﹣1）=0，‎ 即a2﹣3a+2=0，‎ 解得a=1，或a=2；‎ 故答案为：1或2．‎ ‎　‎ ‎14．如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆．在扇形OAB内随机取一点，则此点取自阴影部分的概率是　　．‎ ‎【考点】几何概型．‎ ‎【分析】以面积为测度，计算出阴影的面积，扇形的面积，可求概率．‎ ‎【解答】解：如图，设两个半圆的交点为C，且以AO为直径的半圆以D为圆心，连结OC、CD 设OA=OB=2，则弓形OMC的面积为 S弓形OMC=S扇形OCD﹣SRt△DCO=•π•12﹣×1×1=﹣‎ 所以空白部分面积为S空白=2（S半圆AO﹣2S弓形OMC）=2[•π•12﹣（﹣1）]=2‎ 因此，两块阴影部分面积之和为S阴影=S扇形OAB﹣S空白=π•22﹣2=π﹣2‎ 可得在扇形OAB内随机取一点，此点取自阴影部分的概率为P===．‎ 故答案为：．‎ ‎　‎ ‎15．正实数x，y满足： +=1，则x2+y2﹣10xy的最小值为　﹣36　．‎ ‎【考点】一元二次不等式的解法．‎ ‎【分析】由+=1得x+y=xy，则x2+y2﹣10xy=（xy﹣6）2﹣36，根据二次函数的性质即可求出．‎ ‎【解答】解：由+=1得x+y=xy，‎ 平方得x2+y2+2xy=（xy）2，‎ 即x2+y2=﹣2xy+（xy）2，‎ 则x2+y2﹣10xy=（xy）2﹣2xy﹣10xy=（xy）2﹣12xy=（xy﹣6）2﹣36，‎ 当xy=6时，有最小值，即最小值为﹣36，‎ 故答案为：﹣36．‎ ‎　‎ ‎16．在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是　　．‎ ‎【考点】圆与圆的位置关系及其判定；直线与圆的位置关系．‎ ‎【分析】由于圆C的方程为（x﹣4）2+y2=1，由题意可知，只需（x﹣4）2+y2=1与直线y=kx﹣2有公共点即可．‎ ‎【解答】解：∵圆C的方程为x2+y2﹣8x+15=0，整理得：（x﹣4）2+y2=1，即圆C是以（4，0）为圆心，1为半径的圆；‎ 又直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，‎ ‎∴只需圆C′：（x﹣4）2+y2=1与直线y=kx﹣2有公共点即可．‎ 设圆心C（4，0）到直线y=kx﹣2的距离为d，‎ 则d=≤2，即3k2﹣4k≤0，‎ ‎∴0≤k≤．‎ ‎∴k的最大值是．‎ 故答案为：．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}．‎ ‎（1）求实数a，b的值；‎ ‎（2）解关于x的不等式：＞0（c为常数）．‎ ‎【考点】一元二次不等式的解法．‎ ‎【分析】（1）由题意知1，b为关于x的方程ax2﹣3x+2=0的两根，由韦达定理可得方程组，解出即可；‎ ‎（2）不等式等价于（x﹣c）（x﹣2）＞0，按照对应方程的根2、c的大小关系分三种情况讨论可得；‎ ‎【解答】解：（1）由题意知1，b为关于x的方程ax2﹣3x+2=0的两根，‎ 则，∴a=1，b=2．‎ ‎（2）不等式等价于（x﹣c）（x﹣2）＞0，‎ 所以：当c＞2时解集为{x|x＞c或x＜2}；‎ 当c=2时解集为{x|x≠2，x∈R}；‎ 当c＜2时解集为{x|x＞2或x＜c}．‎ ‎　‎ ‎18．彭山二中决定在新校区附近修建教师宿舍，学校行政办公室用100万元从政府购得一块廉价土地，该土地可以建造每层1000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高20元．已知建筑第5层楼房时，每平方米建筑费用为800元．‎ ‎（1）若建筑第x层楼时，该楼房综合费用为y万元（综合费用是建筑费用与购地费用之和），写出y=f（x）的表达式．‎ ‎（2）为了使该楼房每平方米的平均综合费用最低，学校应把楼层建成几层？此时平均综合费用为每平方米多少元？‎ ‎【考点】函数模型的选择与应用．‎ ‎【分析】（1）第1层楼房每平方米建筑费用为720元，第1层楼房建筑费用为720×1000=720000（元）=72（万元）；‎ 楼房每升高一层，整层楼建筑费用提高20×1000=20000（元）=2（万元）；第x层楼房建筑费用为72+（x﹣1）×2=2x+70（万元）；建筑第x层楼时，楼房综合费用=建筑总费用（等差数列前n项和）+购地费用，由此可得y=f（x）；‎ ‎（2）楼房每平方米的平均综合费用为g（x），则（元），代入（1）中f（x）整理，求出最小值即可．‎ ‎【解答】解：（1）由题意知，建筑第1层楼房每平方米建筑费用为：720元．‎ 建筑第1层楼房建筑费用为：720×1000=720000（元）=72（万元）‎ 楼房每升高一层，整层楼建筑费用提高：20×1000=20000（元）=2（万元）‎ 建筑第x层楼房建筑费用为：72+（x﹣1）×2=2x+70（万元）‎ 建筑第x层楼时，该楼房综合费用为：‎ 所以，y=f（x）=x2+71x+100（x≥1，x∈Z）‎ ‎（2）设该楼房每平方米的平均综合费用为g（x），则：‎ ‎==910，‎ 当且仅当，即x=10时，等号成立；‎ 所以，学校应把楼层建成10层．此时平均综合费用为每平方米910元．‎ ‎　‎ ‎19．过原点且斜率为的直线l1与直线l2：2x+3y﹣1=0交于A点，求过点A且圆心在直线y=﹣2x上，并与直线x+y﹣1=0相切的圆的方程．‎ ‎【考点】圆的切线方程．‎ ‎【分析】求出过原点且斜率为的直线l1的方程与2x+3y﹣1=0联立得A（2，﹣1），设圆方程为（x﹣a）2+（y﹣b）2=r2，圆心（a，b），则﹣2a=b， =r，（2﹣a）2+（﹣1﹣b）2=r2，求出a，b，r，即可求出圆的方程．‎ ‎【解答】解：过原点且斜率为的直线l1的方程为x+2y=0．‎ x+2y=0与2x+3y﹣1=0联立得A（2，﹣1），‎ 设圆方程为（x﹣a）2+（y﹣b）2=r2，圆心（a，b），‎ 则﹣2a=b， =r，（2﹣a）2+（﹣1﹣b）2=r2，‎ 解得a=1 b=﹣2 r=，‎ 所以圆的方程为（x﹣1）2+（y+2）2=2．‎ ‎　‎ ‎20．已知直线x﹣y+1=0与圆C：x2+y2﹣4x﹣2y+m=0交于A，B两点；‎ ‎（1）求线段AB的垂直平分线的方程；‎ ‎（2）若|AB|=2，求m的值；‎ ‎（3）在（2）的条件下，求过点P（4，4）的圆C的切线方程．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】（1）由题意，线段AB的垂直平分线经过圆的圆心（2，1），斜率为﹣1，可得线段AB的垂直平分线的方程．‎ ‎（2）利用|AB|=2，求出圆心到直线的距离，利用点到直线的距离公式求出圆心到直线的距离，从而可求m的值．‎ ‎（3）分类讨论，利用圆心到直线的距离等于半径，即可得出结论．‎ ‎【解答】解：（1）由题意，线段AB的垂直平分线经过圆的圆心（2，1），斜率为﹣1，‎ ‎∴方程为y﹣1=﹣（x﹣2），即x+y﹣3=0；‎ ‎（2）圆x2+y2﹣4x﹣2y+m=0可化为（x﹣2）2+（y﹣1）2=﹣m+5，‎ ‎∵|AB|=2，∴圆心到直线的距离为，‎ ‎∵圆心到直线的距离为d==，∴，∴m=1‎ ‎（3）由题意，知点P（4，4）不在圆上．‎ ‎①当所求切线的斜率存在时，设切线方程为y﹣4=k（x﹣4），即kx﹣y﹣4k+4=0．由圆心到切线的距离等于半径，得=2，‎ 解得k=，所以所求切线的方程为5x﹣12y+28=0‎ ‎②当所求切线的斜率不存在时，切线方程为x=4‎ 综上，所求切线的方程为x=4或5x﹣12y+28=0．‎ ‎　‎ ‎21．为了比较两种治疗失眠症的药（分别成为A药，B药）的疗效，随机地选取20位患者服用A药，20位患者服用B药，这40位患者服用一段时间后，记录他们日平均增加的睡眠时间（单位：h）实验的观测结果如下：‎ 服用A药的20位患者日平均增加的睡眠时间：‎ ‎0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5‎ ‎2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4‎ 服用B药的20位患者日平均增加的睡眠时间：‎ ‎3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4‎ ‎1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5‎ ‎（Ⅰ）分别计算两种药的平均数，从计算结果看，哪种药的疗效更好？‎ ‎（Ⅱ）根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？‎ ‎【考点】众数、中位数、平均数；茎叶图．‎ ‎【分析】（Ⅰ）利用平均数的计算公式即可得出，据此即可判断出结论；‎ ‎（Ⅱ）利用已知数据和茎叶图的结构即可完成．‎ ‎【解答】解：（Ⅰ）设A药观测数据的平均数据的平均数为，设B药观测数据的平均数据的平均数为，‎ 则=×（0.6+1.2+2.7+1.5+2.8+1.8+2.2+2.3+3.2+3.5+2.5+2.6+1.2+2.7+1.5+2.9+3.0+3.1+2.3+2.4）=2.3．‎ ‎×（3.2+1.7+1.9+0.8+0.9+2.4+1.2+2.6+1.3+1.4+1.6+0.5+1.8+0.6+2.1+1.1+2.5+1.2+2.7+0.5）=1.6．‎ 由以上计算结果可知：．由此可看出A药的效果更好．‎ ‎（Ⅱ）根据两组数据得到下面茎叶图：‎ 从以上茎叶图可以看出，A药疗效的试验结果有的叶集中在2，3上．而B药疗效的试验结果由的叶集中在0，1上．由此可看出A药的疗效更好．‎ ‎　‎ ‎22．从某学校高三年级共800名男生中随机抽取50人测量身高．据测量，被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…；第八组[190，195]．如图是按上述分组方法得到的频率分布直方图的一部分．已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．‎ ‎（1）估计这所学校高三年级全体男生身高在180cm以上（含180cm）的人数及平均身高；‎ ‎（2）求第六组、第七组的频率并补充完整频率分布直方图；‎ ‎（3）若从身高属于第六组和第八组的所有男生中随机抽取两人，记他们的身高分别为x、y，求满足“|x﹣y|≤5”的事件的概率．‎ ‎【考点】概率的应用；频率分布直方图；列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）由频率分布直方图可得前五组频率，进而可得后三组频率和人数，又可得后三组的人数，可得平均身高；‎ ‎（2）易得后三组的，可得频率分布直方图；‎ ‎（3）身高在[180，185）内的人数为4，设为a、b、c、d，身高在[190，195]内的人数为2，设为A、B，列举可得总的基本事件共15种情况，事件“|x﹣y|≤5”所包含的基本事件个数有6+1=7，由概率公式可得．‎ ‎【解答】解：（1）由频率分布直方图得前五组频率为（0.008+0.016+0.04+0.04+0.06）×5=0.82，‎ 后三组频率为1﹣0.82=0.18，人数为0.18×50=9，‎ ‎∴学校高三年级全体男生身高在180 cm以上（含180 cm）的人数为800×0.18=144，‎ 由频率分布直方图得第八组频率为0.008×5=0.04，人数为0.04×50=2，‎ 设第六组人数为m，则第七组人数为9﹣2﹣m=7﹣m，‎ 又由等差数列可得m+2=2（7﹣m），解得m=4，‎ ‎∴第六组人数为4，第七组人数为3，‎ ‎∴平均身高为≈186.4‎ ‎（2）由（1）可得第八组频率为0.008×5=0.04，人数为0.04×50=2，‎ 第六组人数为4，第七组人数为3，频率分别等于0.08，0.06．‎ 分别等于0.016，0.012．其完整的频率分布直方图如图．‎ ‎（3）由（2）知身高在[180，185）内的人数为4，设为a、b、c、d，‎ 身高在[190，195]内的人数为2，设为A、B，‎ 若x，y∈[180，185）时，有ab、ac、ad、bc、bd、cd共6种情况；‎ 若x，y∈[190，195]时，有AB共1种情况；‎ 若x，y分别在[180，185）和[190，195]内时，有aA、bA、cA、dA、aB、bB、cB、dB，共8种情况．‎ ‎∴基本事件总数为6+1+8=15，事件“|x﹣y|≤5”所包含的基本事件个数有6+1=7，‎ ‎∴P（|x﹣y|≤5）=．‎