2019-2020学年山西省芮城市高二3月月考数学（文） word版

2019-2020学年山西省芮城市高二3月月考数学（文） word版

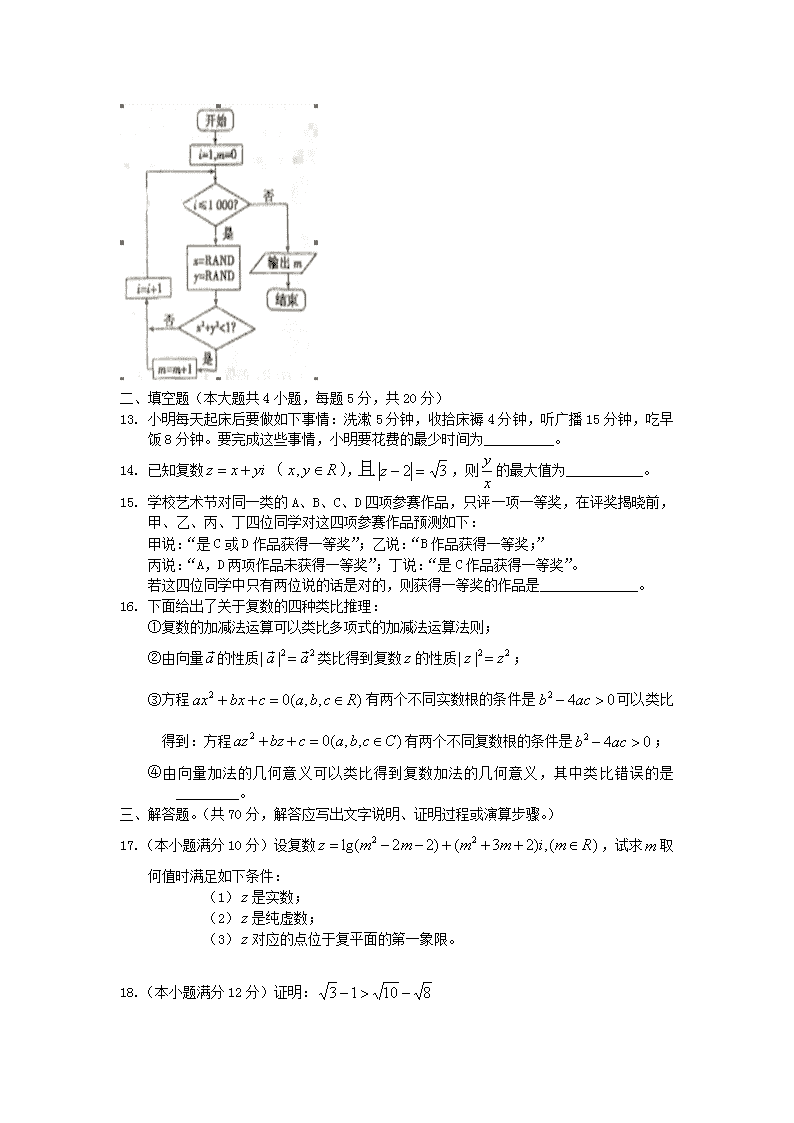
山西省芮城市2019-2020学年高二3月月考数学试题（文科）‎ ‎（考试范围：选修1—2）‎ ‎2020.4‎ 一、 选择题（本大题共12小题，每题5分，共60分）‎ 1. 下列结论正确的是（ ）‎ ‎①函数关系是一种确定性关系。‎ ‎②相关关系是一种非确定性关系。‎ ‎③回归分析是对具有函数关系的两个变量进行统计分析的一种方法。‎ ‎④回归分析是对具有相关关系的两个变量进行统计分析的一种方法。‎ A.①② B.①②③ C.①②④ D.①②③④‎ ‎2. 复数的共轭复数是（ ）‎ ‎ A. B. C. D. ‎ ‎3. 学校教职成员、教师、后勤人员、理科教师、文科教师的结构图正确的是（ ）‎ ‎4. 用反证法证明命题：“三角形三个内角至少有一个不大于60º”时，应假设（ ）‎ ‎ A. 三个内角都不大于60º B. 三个内角都大于60º ‎ C. 三个内角至多有一个大于60º D. 三个内角至多有两个大于60º ‎5. 下面用“三段论”形式写出的演绎推理：因为指数函数且在上是增函数，是指数函数，所以在上是增函数，该结论显然是错误的，其原因是（ ）‎ ‎ ‎ ‎ A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 以上都可能 ‎6.下列表述正确的是（ ）‎ ‎①归纳推理是由特殊到一般的推理； ②演绎推理是由一般到特殊的推理；‎ ‎③类比推理是由特殊到一般的推理； ④分析法是一种间接证明法；‎ ‎ A.②④ B. ①③ C. ①④ D. ①②‎ ‎7.已知、的取值如下表所示：‎ ‎0‎ ‎1‎ ‎3‎ ‎4‎ ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ ‎ 若从散点图分析，与线性相关，且，则的值等于（ ）‎ A.2.6 B. 6.3 C. 2 D. 4.5‎ ‎8.分析法证明不等式的推理过程是寻求使不等式成立的（ ）‎ A.必要条件 B. 充分条件 C. 充要条件 D. 必要条件或充分条件 ‎ ‎9.如图，5个数据，去掉D（3，10）后，‎ 下列说法错误的是（ ）‎ ‎ A. 相关系数r变大 ‎ B. 残差平方和变大 ‎ ‎ C. 相关指数R2变大 ‎ D. 解释变量与预报变量的相关性变强 ‎10. 下列说法正确的是（ ）‎ ‎ A. 在统计学中，回归分析是检验两个分类变量是否有关系的一种统计方法 B. 线性回归方程对应的直线至少经过其样本数据点，‎ ‎ 中的一个点 C.在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高 D.在回归分析中，相关指数为0.98的模型比相关指数为0.80的模型拟合的效果差 ‎11、已知下表： ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎…‎ 则的位置是（ ）‎ A. 第13行第2个数 B. 第14行第3个数 B. 第13行第3个数 D. 第17行第2个数 12. 我们可以用随机数法估计的值，如图所示的程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0,1）内的任何一个实数）.若输出的结果为781，则由此可估计的近似值为（ ）‎ ‎ A.3.119 B.3.124 C.3.132 D.3.151‎ ‎ ‎ 二、填空题（本大题共4小题，每题5分，共20分）‎ ‎13. 小明每天起床后要做如下事情：洗漱5分钟，收拾床褥4分钟，听广播15分钟，吃早饭8分钟。要完成这些事情，小明要花费的最少时间为__________。‎ ‎14. 已知复数（),且，则的最大值为___________。 ‎ ‎15. 学校艺术节对同一类的A、B、C、D四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：‎ 甲说：“是C或D作品获得一等奖”；乙说：“B作品获得一等奖；”‎ 丙说：“A，D两项作品未获得一等奖”；丁说：“是C作品获得一等奖”。‎ 若这四位同学中只有两位说的话是对的，则获得一等奖的作品是______________。‎ 16. 下面给出了关于复数的四种类比推理：‎ ‎①复数的加减法运算可以类比多项式的加减法运算法则；‎ ‎②由向量的性质类比得到复数的性质；‎ ‎③方程有两个不同实数根的条件是可以类比得到：方程有两个不同复数根的条件是；‎ ‎④由向量加法的几何意义可以类比得到复数加法的几何意义，其中类比错误的是_________。‎ 三、解答题。（共70分，解答应写出文字说明、证明过程或演算步骤。） ‎ ‎17. （本小题满分10分）设复数，试求取何值时满足如下条件：‎ ‎（1）是实数；‎ ‎（2）是纯虚数；‎ ‎ （3）对应的点位于复平面的第一象限。‎ ‎18.（本小题满分12分）证明：‎ 19. ‎（本小题满分12分）已知数列的前项和为，满足 ‎ ‎，计算并猜想的表达式。‎ 20. ‎（本小题满分12分）某企业通过调查问卷(满分50分)的形式对本企业900名员工 的 工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:‎ 女 ‎47‎ ‎36‎ ‎32‎ ‎48‎ ‎34‎ ‎44‎ ‎43‎ ‎47‎ ‎46‎ ‎41‎ ‎43‎ ‎42‎ ‎50‎ ‎43‎ ‎35‎ ‎49‎ 男 ‎37‎ ‎35‎ ‎34‎ ‎43‎ ‎46‎ ‎36‎ ‎38‎ ‎40‎ ‎39‎ ‎32‎ ‎48‎ ‎33‎ ‎40‎ ‎34‎ ‎ ‎ ‎ ‎ ‎(1)根据以上数据,估计该企业得分大于45分的员工人数; (2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为‘满意’,否则为“不满意”,请完成下列表格:‎ ‎ ‎ ‎“满意”的人数 ‎“不满意”人数 合计 女 ‎ ‎ ‎ ‎ ‎16‎ 男 ‎ ‎ ‎ ‎ ‎14‎ 合计 ‎ ‎ ‎ ‎ ‎30‎ ‎〔3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关? ‎ 参考数据:‎ ‎0.10‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ k ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎21.设，用综合法证明：。‎ ‎22.（共12分）禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数（个）随时间（天）变化的规律，收集数据如下 天数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 繁殖个数 ‎6‎ ‎12‎ ‎25‎ ‎49‎ ‎95‎ ‎190‎ 作出散点图可看出样本点分布在一条指数型函数的周围 保留小数点后两位数的数的参考数据： ‎ ‎ （1）求出关于的回归方程（保留小数点后两位数字）； （2）已知，估算第四天的残差。‎ 参考公式：‎ ‎ ‎ 文数参考答案 ‎ ‎ 一、选择题（本大题共12小题，每题5分，共60分）‎ ‎1—5CDABA 6—10 DABBC 11—12 CB 二、填空题（本大题共4小题，每题5分，共20分） ‎ ‎13. 17 14. 15. B 16. ②③‎ 三、解答题。（共70分)‎ ‎17、（10分）‎ 解:(1)当复数的虚部且时,即,或时,复数表示实数.…………3分 (2)当实部等于零且虚部不等于零时,复数表示实数.由,且,求得,或且且,故当时,复数为纯虚数.………………3分 (3)由,且时,复数对应的点位于复平面的第一象限. 解得,或,‎ 故当,或时,复数对应的点位于复平面的第一象限.………………4分 ‎……4分 ‎18、（12分） 证明:要证，‎ ‎……2分 只需证:, 只要证:, 即证: 只需证:, 即证:‎ ‎, 该式显然成立, 所以得证。‎ ‎19. （12分）‎ ‎20. （12分）‎ ‎21.（12分）证明如下：‎ ‎22. （12分）‎ ‎ ‎