- 2021-06-21 发布 |
- 37.5 KB |
- 14页


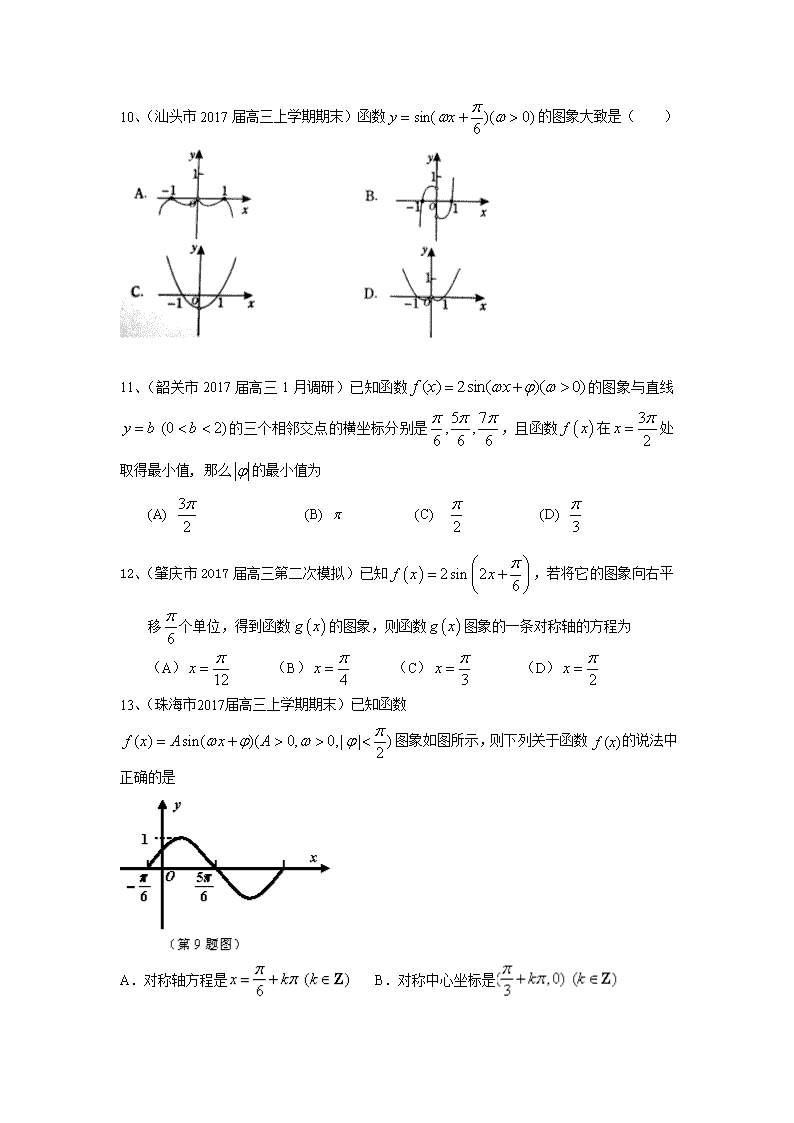
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广东省13市2017届高三上学期期末考试数学理试题分类汇编:三角函数 Word版
广东省13市2017届高三上学期期末考试数学理试题分类汇编 三角函数 一、选择、填空题 1、(潮州市2017届高三上学期期末)若=﹣,则sin(α+)的值为( ) A. B.﹣ C. D.﹣ 2、(东莞市2017届高三上学期期末)已知函数的最小正周期为,将函数的图象向右平移个所得图象对应的函数为,则关于函数为的性质,下列说法不正确的是( ) A.g(x)为奇函数 B.关于直线对称 C.关于点(,0)对称 D.在上递增 3、(佛山市2017届高三教学质量检测(一))下列函数中,同时满足两个条件“①,;②当时,”的一个函数是( ) A. B. C. D. 4、(广州市2017届高三12月模拟)若将函数的图象向左平移个单位,所得图象关于轴对称,则的最小正值是 (A) (B) (C) (D) 5、(惠州市2017届高三第三次调研)函数y=cos 2x+2sin x的最大值为( ) (A) (B)1 (C) (D)2 6、(江门市2017届高三12月调研)已知函数 ,则下列说法正确的是 A.的图象向右平移个单位长度后得到的图象 B.若,则, C.的图象关于直线对称 D.的图象关于点对称 7、(茂名市2017届高三第一次综合测试)如图1,函数)的图象过点,则的图象的一个对称中心是( ) A. B. C. D. 8、(清远市清城区2017届高三上学期期末)函数的最小正周期是,若其图象向右平移个单位后得到的函数为奇函数,则函数的图象( ) A.关于点对称 B.关于对称C.关于点对称 D.关于对称 9、(汕头市2017届高三上学期期末)函数的图象与轴正半轴交点的横坐标构成一个公差为的等差数列,若要得到函数的图象,只要将的图象( )个单位 A.向左平移 B.向左平移 C. 向左平移 D.向左平移 10、(汕头市2017届高三上学期期末)函数的图象大致是( ) 11、(韶关市2017届高三1月调研)已知函数的图象与直线的三个相邻交点的横坐标分别是,且函数在处取得最小值, 那么的最小值为 (A) (B) (C) (D) 12、(肇庆市2017届高三第二次模拟)已知,若将它的图象向右平移个单位,得到函数的图象,则函数图象的一条对称轴的方程为 (A) (B) (C) (D) 13、(珠海市2017届高三上学期期末)已知函数图象如图所示,则下列关于函数 f (x)的说法中正确的是 A.对称轴方程是 B.对称中心坐标是 C.在区间上单调递增 D.在区间上单调递减 14、(惠州市2017届高三第三次调研)在中,角的对边分别是,已知,且,则的面积为_____________. 二、解答题 1、(潮州市2017届高三上学期期末)在△ABC中,a,b,c分别是角A,B,C的对边,=(a,c)与=(1+cosA,sinC)为共线向量. (1)求角A; (2)若3bc=16﹣a2,且S△ABC=,求b,c的值. 2、(东莞市2017届高三上学期期末)设△ABC 的内角 A, B,C 的对边分别是a,b, c,且a =b cosC +c sin B。 (Ⅰ)求角B 的大小; (Ⅱ)若点M 为BC的中点,且 AM =AC,求sin∠BAC 3、(佛山市2017届高三教学质量检测(一)) 中的内角的对边分别为,若, (Ⅰ)求;(Ⅱ)若,点为边上一点,且,求的面积 4、(广州市2017届高三12月模拟) 已知△的内角,,的对边分别为,,,若,. (Ⅰ)求; (Ⅱ)若, 求. 5、(江门市2017届高三12月调研)已知是锐角三角形,内角所对的边分别是,满足. (Ⅰ)求角的值; (Ⅱ)若,,求的周长. 6、(揭阳市2017届高三上学期期末)在△ABC中,、、分别为角、、所对的边,,且. (Ⅰ)求角的大小; (Ⅱ)求△ABC外接圆的圆心到AC边的距离. 7、(茂名市2017届高三第一次综合测试)已知函数. (Ⅰ)求函数f(x)的最小正周期、最大值及取得最大值时x的集合; (Ⅱ)设△ABC内角A、B、C的对边分别为,若,b=1,, 且,求角B和角C. 8、(韶关市2017届高三1月调研)如图,在中,是边的中点,,. (Ⅰ)求角的大小; (Ⅱ)若角,边上的中线的长为,求的面积. 9、(肇庆市2017届高三第二次模拟)的内角A,B,C的对边分别为a,b,c,已知 . (Ⅰ)求角C; (Ⅱ)若,的面积为,求的周长. 参考答案 一、选择、填空题 1、【解答】解:∵= ==﹣2cos(﹣α)=﹣2sin(α+), ∴﹣2sin(α+)=﹣, ∴sin(α+)=. 故选:C. 2、B 3、C 4、A 5、【解析】 y=cos 2x+2sin x=-2sin2x+2sin x+1, 设t=sin x(-1≤t≤1),则原函数可以化为y=-2t2+2t+1=-22+, ∴当t=时,函数取得最大值. 6、C 7、B 解:由函数图象可知:A = 2,由于图象过点(0,),可得: ,即,由于|φ|<,解得:φ=,即有:f(x)=2sin(2x+ ).由2 x + =kπ,k∈Z可解得:x =,k∈Z,故f(x)的图象的对称中心是:(,0),k∈Z,当k=0时,f(x)的图象的对称中心是:(,0). 8、A 9、D 10、D 11、【解析】已知函数的图象与直线的三个相邻交点的横坐标分别是,则函数的周期为,,又函数在处取得最小值,则,所以,故的最小值为,故选C 12、C 13、D 14.【解析】由正弦定理,又,且, 所以,所以, 所以 二、解答题 1、【解答】解:(1)由已知得asinC=c(cosA+1), ∴由正弦定理得sinAsinC=sinC(cosA+1),. …(2分) ∴sinA﹣cosA=1,故sin(A﹣)=.… 由0<A<π,得A=; … (2)在△ABC中,16﹣3bc=b2+c2﹣bc, ∴(b+c)2=16,故b+c=4. ①…(9分) 又S△ABC==bc, ∴bc=4.②…(11分) 联立①②式解得b=c=2.…(12分) 2、 解:(Ⅰ) 由正弦定理 …………1分 有 …………2分 又即 …………3分 …………4分 …………5分 因为 …………6分 (Ⅱ)解法一:设则 …………7分 中, …………8分 中, …………9分 …………10分 …………11分 由平方关系得 …………12分 解法二:取中点,连接,则 …………7分 设,则 …………8分 由(Ⅰ)知, …………10分 由 …………11分 由平方关系得 …………12分 解法三:由题知,, 在与中,由余弦定理得 …………8分 即 …………11分 由正弦定理得 …………12分 3、 4、(Ⅰ)因为,, 由余弦定理得,即. ……………………2分 所以. …………………………………………4分 由于, 所以. …………………………………………6分 (Ⅱ)法1: 由及, 得, ……………………7分 即, ………………………………………………………………8分 解得或(舍去). …………………………………………9分 由正弦定理得, …………………………………………10分 得. ………………………………………12分 法2: 由及正弦定理得, …………………………………………7分 得. …………………………………………8分 由于, 则, 则. …………………………………………9分 由于, 则. ………………………………………10分 所以 ………………………………………11分 . ……………………………………………………………12分 5、解:⑴……1分 ……3分 所以……4分 又A为锐角,所以……6分 ⑵由,得 ①……7分 由⑴知,所以bc=24 ②……8分 由余弦定理知a2=b2+c2-2bccosA,将及①代入可得c2+b2=52③……10分 ③+②×2,得(c+b)2=100,所以c+b=10,△ABC的周长是……12分 6、解:(Ⅰ)由,结合余弦定理得: ,-------------------------------------------------------------------------------2分 ,----------------------------------------------------------------------------------3分 则,-----------------------------------------------------5分 ∵ ∴. ---------------------------------------------------------------------------7分 (Ⅱ) 设△ABC外接圆的半径为R,由正弦定理知 ,-------------------------------------------------------------------9分 故,-------------------------------------------------------------------------------------------10分 则△ABC外接圆的圆心到AC边的距离.---------------------------------------------------------------12分 7、解:(Ⅰ) ……………………………1分 ……………………………2分 函数f(x)的最小正周期为 …………………………………………3分 当,即时,f(x)取最大值为, ………4分 这时x的集合为 …………………………………………5分 (Ⅱ) ………………………6分 ………………………………………………7分 ………………………………………………8分 …………………………………………………………9分 …………………………………10分 …………………………………………………………………11分 ……………………………………………………………………12分 8、解:(Ⅰ)由题意可知, 又 ……… 1分 所以, ……………2分 ……4分 , 又, 所以.…………………6分 (Ⅱ)由(1)知,且 所以,,则 …………7分 设,则 在中由余弦定理得, …………9分 解得 ……………………10分 故. ……………………12分 9、解:(Ⅰ)由已知以及正弦定理,得, (2分) 即. (3分) 所以, (5分) 又,所以. (6分) (Ⅱ)由(Ⅰ)知,所以, (8分) 又,所以, (9分) 所以,即. (11分) 所以周长为. (12分)查看更多