数学卷·2018届青海省西宁二十一中高三11月月考（2017

数学卷·2018届青海省西宁二十一中高三11月月考（2017

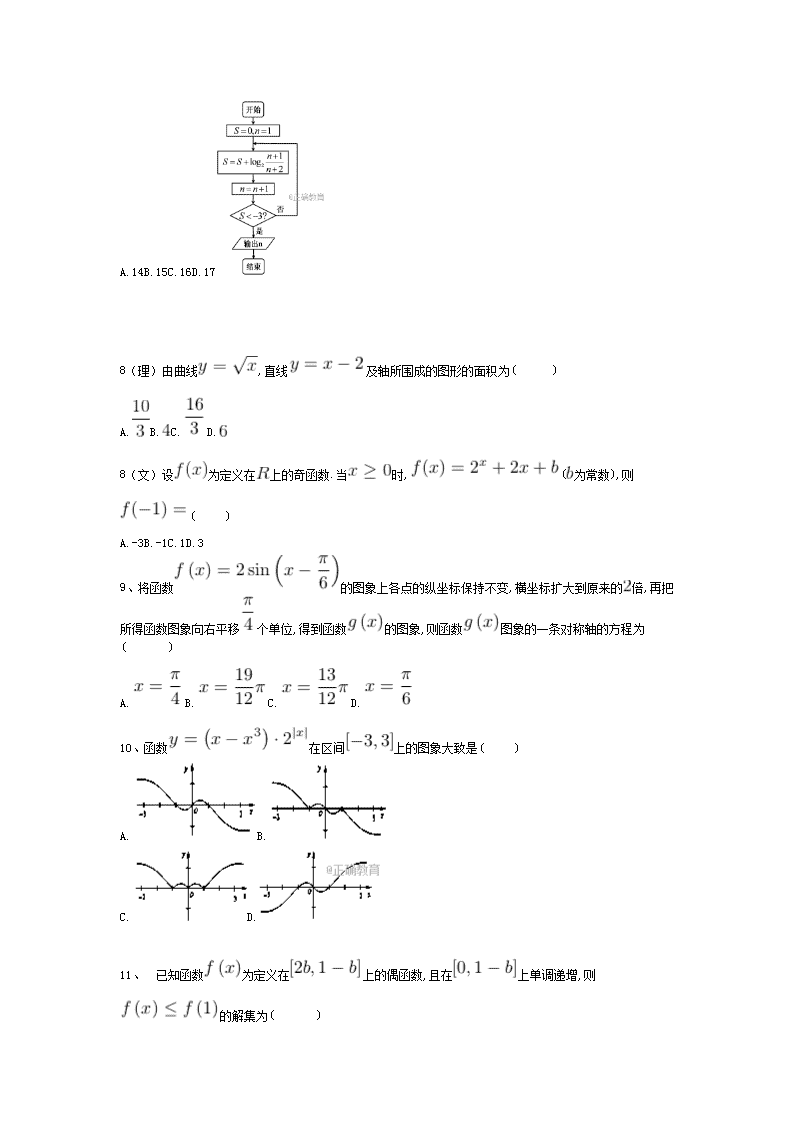
‎ 考场： 考号： 姓名： 班级：‎ 西宁市第二十一中学2017-2018学年第一学期 高三理科数学十一月检测试卷 试卷满分：150分 考试时间：120分钟 命题人：高三数学备课组 审核人：‎ 一、 选择题（每小题5分，共12题，小计60分）‎ ‎1、已知集合,集合,则(    )‎ A.B.‎ C.D.‎ ‎2、已知复数满足,则z在复平面上对应的点位于(   )‎ A.第一象限B.第二象限C.第三象限D.第四象限 ‎3、已知为第二象限角,,则(    )‎ A.B.C.D.‎ ‎4、已知向量,,若,则实数的值为(    )‎ A.2B.-2C.1D.-1‎ ‎5、已知数列中,,,则等于(    )‎ A.B.C.D.‎ ‎6、在中,角、、的对边分别为、、,若,则角的值为(   ) A.B.C.或D.或 7、 执行如图所示的程序框图,则输出的结果是(   )‎ A.14B.15C.16D.17‎ ‎ ‎ ‎8（理）由曲线,直线及轴所围成的图形的面积为(    )‎ A.B.C.D.‎ ‎8（文）设为定义在上的奇函数.当时,(为常数),则(   ) A.-3B.-1C.1D.3‎ ‎9、将函数的图象上各点的纵坐标保持不变,横坐标扩大到原来的倍,再把所得函数图象向右平移个单位,得到函数的图象,则函数图象的一条对称轴的方程为(    )‎ A.B.C.D.‎ ‎10、函数在区间上的图象大致是(   )‎ A.B.‎ C.D.‎ ‎11、 已知函数为定义在上的偶函数,且在上单调递增,则的解集为(    )‎ A.B.C.D.‎ ‎12、 已知是函数的导函数,且对任意的实数都有(是自然对数的底数),,若不等式的解集中恰有两个整数,则实数的取值范围是(     )‎ A.B.C.D.‎ 二、填空题（每题5分，共4题，小计20分）‎ ‎13、在中,若,,,则        .‎ ‎14、已知是等差数列,为其前项和,.若,,则的值为.‎ ‎15、已知数列是递增的等比数列,,,则数列的前项和等于        .‎ ‎16、已知函数满足下列条件:‎ ‎①周期;‎ ‎②图象向右平移个单位长度后对应函数为偶函数;‎ ‎③.‎ 则函数的解析式        .‎ 三、解答题 17(理)已知是等差数列,是等比数列,且,,,. 1.求的通项公式; 2.设,求数列的前项和.‎ ‎17（文）已知等差数列中,,, 1.求数列的通项公式; 2.若数列的前项和,求的值.‎ ‎18（理）在中,角,,的对边分别为,,,若.‎ ‎1.求的大小;‎ ‎2.若,且,求的值。‎ ‎18（文）已知的内角所对的边分别为.向量与平行.‎ ‎1.求;‎ ‎2.若,求的面积.‎ ‎19（理）已知函数,且当时,的最小值为.‎ ‎1.求的值,并求的单调递增区间;‎ ‎2.先将函数的图象上的点纵坐标不变,横坐标缩小到原来的,再将所得图象向右平移个单位,得到函数的图象,求方程在区间上所有根之和.‎ ‎19（文）已知函数.‎ ‎1.求的最小正周期;‎ ‎2.判断函数在上的单调性.‎ ‎20（理）2017年3月智能共享单车项目正式登陆某市,两种车型(“小绿车”、“小黄车”)采用分时段计费的方式,“小绿车”每分钟收费元(不足分钟的部分按分钟计算);“小黄车”每分钟收费元(不足分钟的部分按分钟计算).有甲、乙、丙三人相互独立的到租车点租车骑行(各租一车一次).设甲、乙、丙不超过分钟还车的概率分别为,三人租车时间都不会超过 分钟.甲、乙均租用“小绿车”版单车,丙租用“小黄车”. 1.求甲、乙两人所付的费用之和等于丙所付的费用的概率; 2.设甲、乙、丙三人所付的费用之和为随机变量,求的分布列和数学期望.‎ ‎20 (文) 有关2013年住房、就业、就医、物价教育依然是全国人民最关心的几大民生问题，某市医疗保险实行定点医疗制度，按照“就近就医”方便管理的原则，参加保险的人员可自主选择四家医疗保险定点医院和一定社区医院作为本人就诊的医疗机构，若甲、乙两名参加保险人员所在地区附近有A、B、C三家社区医院，并且他们对社区医院的选择互不影响。‎ （1） 求甲选择A社区医院的概率 （2） 求甲乙两人选择同一家社区医院的概率。‎ ‎ ‎ ‎21（理）已知函数.‎ ‎1.求函数的单调递增区间;‎ ‎2.若,,且对于任意的,都有成立,求实数的取值范围.‎ ‎21（文）已知函数在处有极值.‎ ‎1.求的值;‎ ‎2.判断函数的单调性并求出单调区间.‎ ‎22、平面直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.‎ ‎1.写出直线的极坐标方程与曲线的直角坐标方程;‎ ‎2.已知与直线平行的直线过点,且与曲线交于两点,试求.‎ 数学试卷 学校：___________姓名：___________班级：___________考号：__________ ‎ ‎ 一、选择题 ‎ ‎1、已知集合,集合,则(    )‎ A. B.‎ C. D.‎ ‎ ‎ 答案： C ‎ ‎ ‎2、已知复数满足,则z在复平面上对应的点位于(   )‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎ ‎ 答案： D ‎ ‎ ‎3、已知为第二象限角,,则(    )‎ A. B. C. D.‎ ‎ ‎ 答案： A ‎4、已知向量,,若,则实数的值为(    )‎ A.2 B.-2 C.1 D.-1‎ ‎ 答案： D ‎ ‎ ‎5、已知数列中,,,则等于(    )‎ A. B. C. D.‎ ‎ ‎ 答案： C ‎ ‎ ‎6、在中,角、、的对边分别为、、,若,则角的值为(   ) A. B. C.或 D.或 答案： A ‎ ‎ ‎7、执行如图所示的程序框图,则输出的结果是(   )‎ ‎ ‎ A.14 B.15 C.16 D.17‎ ‎ ‎ 答案： C ‎8（理）由曲线,直线及轴所围成的图形的面积为(    )‎ A. B. C. D.‎ ‎ ‎ 答案： A ‎8（文）设为定义在上的奇函数.当时,(为常数),则(   ) A.-3 B.-1 C.1 D.3‎ ‎ 答案： A ‎ 9、将函数的图象上各点的纵坐标保持不变,横坐标扩大到原来的倍,再把所得函数图象向右平移个单位,得到函数的图象,则函数图象的一条对称轴的方程为(    )‎ A. B. C. D.‎ ‎ ‎ 答案： B ‎ 10、函数在区间上的图象大致是(   )‎ A. B.‎ C. D.‎ ‎ ‎ 答案： A ‎ 11、 已知函数为定义在上的偶函数,且在上单调递增,则的解集为(    )‎ A. B. C. D.‎ ‎ ‎ 答案： C ‎12、 已知是函数的导函数,且对任意的实数都有(是自然对数的底数),,若不等式的解集中恰有两个整数,则实数的取值范围是(     )‎ A. B. C. D.‎ ‎ ‎ 答案： C ‎ ‎ 二、填空题 ‎13、在中,若,,,则        .‎ ‎ 答案： ‎ ‎14、已知是等差数列,为其前项和,.若,,则的值为 .‎ ‎ 答案： 110‎ ‎15、已知数列是递增的等比数列,,,则数列的前项和等于        .‎ ‎ 答案： ‎ ‎16、已知函数满足下列条件:‎ ‎①周期;‎ ‎②图象向右平移个单位长度后对应函数为偶函数;‎ ‎③.‎ 则函数的解析式        .‎ 三、解答题 17、已知是等差数列,是等比数列,且,,,. 1.求的通项公式; 2.设,求数列的前项和.‎ ‎ 答案： 1.等比数列的公比, 所以,, 设等差数列的公差为, 因为,, 所以,即, 所以 ‎ 2.由知,,, 因此, 从而数列的前项和 .‎ ‎ ‎ 解析： 1.求出等比数列的公比,求出,的值,根据等差数列的通项公式求解; 2.根据等差数列和等比数列的前项和公式求数列的前项和. 考点:等差、等比数列的通项公式和前项和公式,考查运算能力. 【名师点睛】1、数列的通项公式及前项和公式都可以看作项数的函数,是函数思想在数列中的应用.数列以通项为纲,数列的问题,最终归结为对数列通项的研究,而数列的前项和可视为数列的通项.通项及求和是数列中最基本也是最重要的问题之一;2、数列的综合问题涉及到的数学思想:函数与方程思想(如:求最值或基本量)、转化与化归思想(如:求和或应用)、特殊到一般思想(如:求通项公式)、分类讨论思想(如:等比数列求和,或)等.‎ ‎17（文）已知等差数列中,,, 1.求数列的通项公式; 2.若数列的前项和,求的值.‎ ‎ 答案： 1.设等差数列的公差为,则, 由于, 又, 所以. 因此. 2.由,得 ‎, 所以, 即, 解得或, 又因为,所以.‎ ‎ ‎ ‎18（理）在中,角,,的对边分别为,,,若.‎ ‎1.求的大小;‎ ‎2.若,且,求的值。‎ ‎ 答案： 1.∵,则 ‎ 2.由得,, . ①‎ 又由余弦定理得,.  ②‎ 由①、②得, .‎ ‎18（文）已知的内角所对的边分别为.向量与平行.‎ ‎1.求;‎ ‎2.若,求的面积.‎ ‎ 答案： 1.因为,所以,‎ 由正弦定理,得,‎ 又,从而,‎ 由于,所以. 2.法一:由余弦定理,及,‎ 得(另一根小于舍去).‎ 故的面积为.‎ 法二:由正弦定理,得,‎ 又由,知,所以.‎ 故.‎ 所以的面积为.‎ ‎19、已知函数,且当时,的最小值为.‎ ‎1.求的值,并求的单调递增区间;‎ ‎2.先将函数的图象上的点纵坐标不变,横坐标缩小到原来的,再将所得图象向右平移个单位,得到函数的图象,求方程在区间上所有根之和.‎ ‎ ‎ 答案： 1.,‎ ‎∵,∴,‎ ‎∴的最小值为,解得.‎ ‎∴.‎ 由,可得,‎ ‎∴的单调递增区间为. 2.由函数图象变换可得,由可得,∴或,解得或,,∴或.∴所有根之和为.‎ ‎19（文）已知函数.‎ ‎1.求的最小正周期;‎ ‎2.判断函数在上的单调性.‎ ‎ ‎ ‎ ‎ 答案： 1.由题意知 ‎,‎ ‎∴的最小正周期. 2.∵,‎ ‎∴时,,∴,‎ 当时,即时,单调递减,‎ 当时,即时,单调递增.‎ ‎ ‎ ‎ ‎ ‎20、2017年3月智能共享单车项目正式登陆某市,两种车型(“小绿车”、“小黄车”)采用分时段计费的方式,“小绿车”每分钟收费元(不足分钟的部分按分钟计算);“小黄车”每分钟收费元(不足分钟的部分按分钟计算).有甲、乙、丙三人相互独立的到租车点租车骑行(各租一车一次).设甲、乙、丙不超过分钟还车的概率分别为,三人租车时间都不会超过分钟.甲、乙均租用“小绿车”版单车,丙租用“小黄车”. 1.求甲、乙两人所付的费用之和等于丙所付的费用的概率; 2.设甲、乙、丙三人所付的费用之和为随机变量,求的分布列和数学期望.‎ ‎ ‎ ‎ ‎ 答案： 1.由题意得,甲乙丙在分钟以上且不超过分钟还车的概率分别为,‎ 记甲、乙两人所付的费用之和等于丙所付费用为事件,‎ 则. 2.可能取值有,‎ ‎;;‎ ‎;‎ ‎;‎ ‎.‎ 甲、乙、丙三人所付的租车费用之和的分布列为 所以.‎ ‎20(文科) 有关2013年住房、就业、就医、物价教育依然是全国人民最关心的几大民生问题，某市医疗保险实行定点医疗制度，按照“就近就医”方便管理的原则，参加保险的人员可自主选择四家医疗保险定点医院和一定社区医院作为本人就诊的医疗机构，若甲、乙两名参加保险人员所在地区附近有A、B、C三家社区医院，并且他们对社区医院的选择互不影响。‎ （1） 求甲选择A社区医院的概率 （2） 求甲乙两人选择同一家社区医院的概率。‎ ‎21（理）已知函数.‎ ‎1.求函数的单调递增区间;‎ ‎2.若,,且对于任意的,都有成立,求实数的取值范围.‎ 答案： 1.依题意,,‎ 令,解得,‎ 故函数的单调递增区间为. 2.当,对任意的,都有;‎ 当时,对任意的,都有;‎ 故对恒成立,或对恒成立,‎ 而,设函数,.‎ 则对恒成立,或对恒成立,.‎ ‎①当时,∵,∴,∴恒成立,‎ ‎∴在上单调递增,,‎ 故在上恒成立,符合题意.‎ ‎②当时,令,得,令,得,‎ 故在上单调递减,‎ 所以, 而,设函数,,‎ 则,‎ 令,则()恒成立,‎ ‎∴在上单调递增,∴恒成立,‎ ‎∴在上单调递增,∴恒成立,‎ 即,而,不合题意.‎ 综上,故实数的取值范围为.‎ ‎21（文）已知函数在处有极值.‎ ‎1.求的值;‎ ‎2.判断函数的单调性并求出单调区间.‎ 答案： 1.,‎ 由题意 2.函数定义域为,‎ 令,‎ ‎∴单增区间为;‎ 令,‎ ‎∴单减区间为.‎ ‎22、平面直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.‎ ‎1.写出直线的极坐标方程与曲线的直角坐标方程;‎ ‎2.已知与直线平行的直线过点,且与曲线交于两点,试求.‎ ‎ ‎ 答案： 1.把直线的参数方程化为普通方程为,∵,∴直线的极坐标方程为,由,可得,‎ ‎∴曲线的直角坐标方程为. 2.直线的倾斜角为,‎ ‎∴直线的倾斜角也为,又直线过点,‎ ‎∴直线的参数方程为(为参数),‎ 将其代入曲线的直角坐标方程可得,‎ 设点对应的参数分别为.‎ 由一元二次方程的根与系数的关系知,.‎ ‎∴.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎