2019-2020学年河北省张家口市高二上学期10月阶段测试 数学 Word版
张家口市2019-2020学年第一学期阶段测试卷
高二数学
考试说明:
1.本试卷共150分。考试时间120分钟;
2.请将各题答案填在答题卡上;
3.本试卷主要考试内容:必修三+选修2-1。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共10个小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
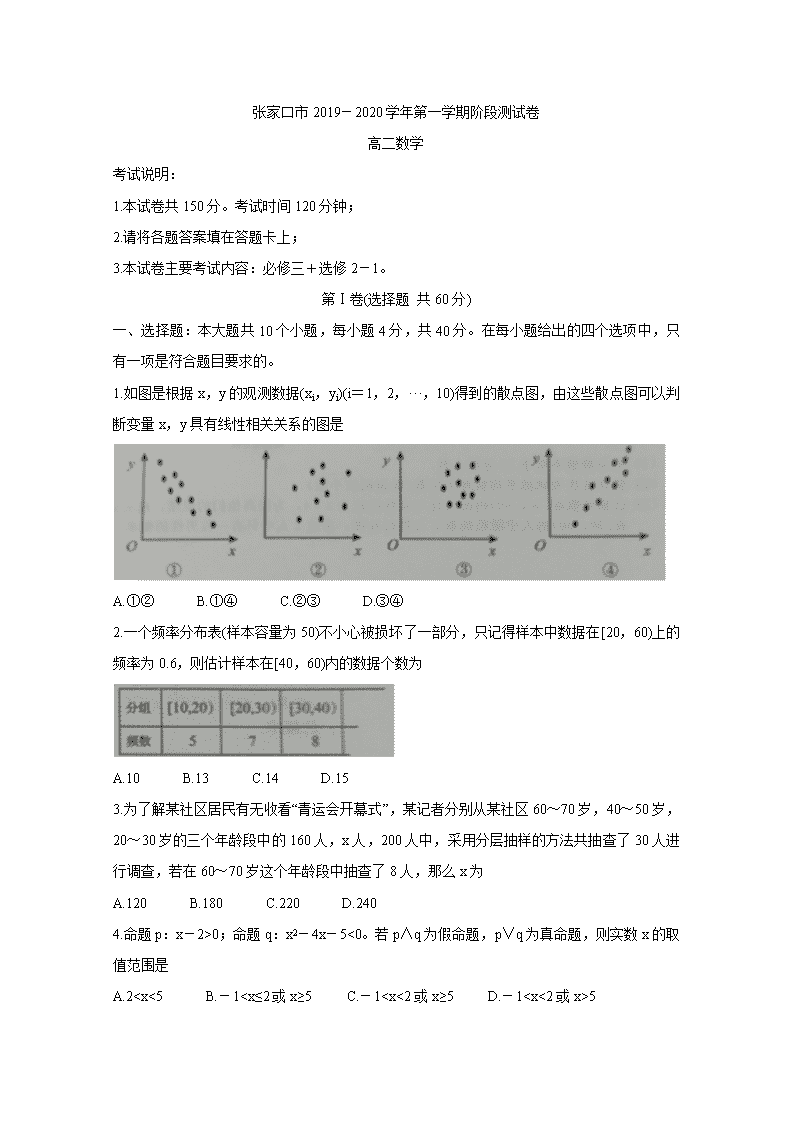
1.如图是根据x,y的观测数据(xi,yi)(i=1,2,···,10)得到的散点图,由这些散点图可以判断变量x,y具有线性相关关系的图是
A.①② B.①④ C.②③ D.③④
2.一个频率分布表(样本容量为50)不小心被损坏了一部分,只记得样本中数据在[20,60)上的频率为0.6,则估计样本在[40,60)内的数据个数为
A.10 B.13 C.14 D.15
3.为了解某社区居民有无收看“青运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,x人,200人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为
A.120 B.180 C.220 D.240
4.命题p:x-2>0;命题q:x2-4x-5<0。若p∧q为假命题,p∨q为真命题,则实数x的取值范围是
A.2
5
5.下面的茎叶图表示的是甲乙两人在5次综合测评中的成绩,其中一个数字被污损,已知甲、乙的平均成绩相同,则被污损的数字为
A.7 B.8 C.9 D.0
6.从一批产品中取出四件产品,设A=“四件产品全不是次品”,B=“四件产品全是次品”,C=“四件产品至少有一件是次品”,则下列结论正确的是
A.A与C互斥 B.任何两个均互斥 C.B与C互斥 D.任何两个均不互斥
7.已知函数f(x)=log2(x+2),若[-1,5]在上随机取一个实数x0,则f(x0)≥1的概率为
A. B. C. D.
8.从集合A={1,3,5,7,9}和集合B={2,4,6,8}中各取一个数,那么这两个数之和能被3整除的概率是
A. B. C. D.
9.下列判断正确的个数是
①“ω=1”是函数f(x)=sinωx-cosωx的最小正周期为2π的充分不必要条件
②若为真命题,则p,q均为假命题
③命题的否定是:
A.0 B.1 C.2 D.3
10.为激发学生学习兴趣,老师上课时在板上写出三个集合:,B={x|x2-4x-5≤0},,然后请甲、乙、丙三位同学到讲台上,并将“△”中的数告诉了他们,要求他们各用一句话来描述,以便同学们能确定该数,以下是甲、乙、丙三位同学的描述,甲:此数为小于的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件。若三位同学说的都对,则“△”中的数为
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.(4分)某班级有60名学生,现采取系统抽样的方法在这60名学生中抽取10名,将这60名学生随机编号1~60号,并分组,第一组1~6,第二组7~12,···,第十组55~60,若在第三组中抽得的号码为14号的学生,则在第八组中抽得的号码为_____的学生。
12.(6分)曙光中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六段[40,50),[50,60),···,[90,100]后画出如下部分率分布直方图,则第四小组的率为_______,从成绩是[40,50)和[90,100]的学生中选两人,他们在同一分数段的概率_______。
13.(4分)如图为中国古代刘徽的《九章算术注》中研究“勾股容方”问题的图形,图中△ABC为直角三角形,四边形DEFC为它的内接正方形,已知BC=3,AC=6,在△ABC上任取一点,则此点取自正方形DEFC的概率为 。
14.(6分)某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数,得到如下数据:
由表中根据12月2日至12月4日的数据,求得线性回归方程中的,则为______,若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,则求得的线性回归方程________。(填“可靠”或“不可靠”)
15.(4分)已知p:-40,若是的充分条件,则实数a的取值范围是 。
16.(6分)已知直线l:y=k(x+1),l与圆C:(x-1)2+y2=3相交于A、B两点,k
的取值范围为_______,弦长|AB|≥2的概率为 。
17.(6分)将两颗正方体型骰子投掷一次,则向上的点数之和是10的概率为 ,向上的点数之和不小于10的概率为 。
18.解答题:本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18(本小题满分14分)已知m∈R,命题p:对任意x∈[0,1],不等式log2(x+1)-2≥m2-3m恒成立;命题q:存在x∈[-1,1],使得成立。
(1)若p为真命题,求m的取值范围;
(2)若p∧q为假,p∨q为真,求m的取值范围。
19.(15分)抽样得到某次考试中高二年级某班6名学生的数学成绩和物理成绩如下表:
(1)在图中画出表中致据的散点图;
(2)建立y关于x的回归方程;(系数保留到小数点后两位)。
(3)如果某学生的数学成绩为83分,预测他本次的物理成绩(成绩取整数)。
(参考公式:回归直线方程为,,。参考数据:)
20.(15分)某校高二年级组织了一次专题培训,从参加考试的学生中抽出100名学生,将其成绩(均分整数)分成为[50,60), [60,70), [70,80), [80,90), [90,100)分为5组,得到如图所示的频率分布直方图。
(1)求分数值不低于70分的人数。
(2)估计这次考试的平均数和中位数(保留两位小数)
(3)已知分数在[50,60)内的男性与女性的比为3:4,为提高他们的成绩,现从分数在[50,60)的人中随机抽取2人进行补课,求这2人中只有一位男性的概率。
21.(15分)己知函数f(x)=ax2-bx+1。
(1)若a,b都是从集合{0,1,2,3}中任取的一个数,求函数f(x)没有零点的概率。
(2)分别从集合P和Q中随机取一个数a和b得到数对(a,b).若P={x|1≤x≤3,x∈R},Q={x|0≤x≤4,x∈R},求函数y=f(x)在区间[1,+∞)上是增函数的概率。
22.(15分)某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人5次数学考试的成绩,统计结果如下表:
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由。
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰。
已知学生甲、乙都只会5道备选题中的3道,那么你推荐的选手选择哪种答题方案进入复赛的可能性更大?并说明理由。