2018届二轮复习1-1集合的概念与运算课件(全国通用)
1
.
1
集合的概念与运算
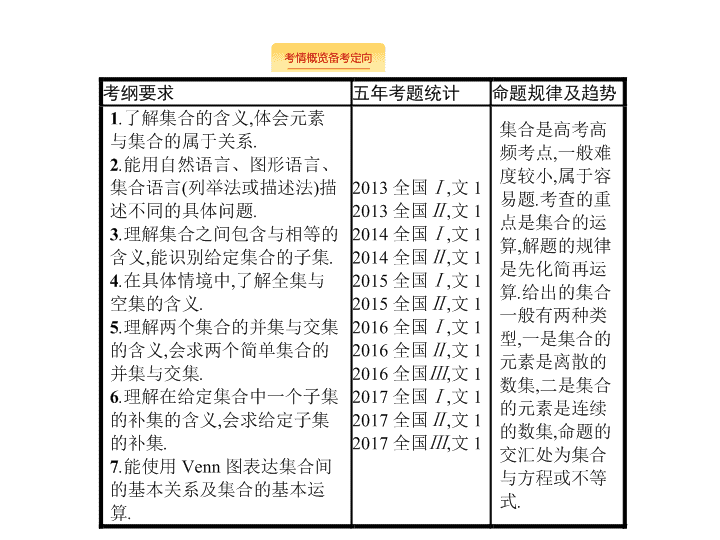
考情概览备考定向
必备知识预案自诊
3
知识梳理
考点自测
1
.
集合的含义与表示
(1)
集合元素的三个特征
:
、
、
.
(2)
元素与集合的关系有
或
两种
,
用符号
或
表示
.
(3)
集合的表示方法
:
、
、
.
(4)
常见数集的记法
.
确定性
互异性
无序性
属于
不属于
∈
∉
列举法
描述法
Venn
图法
N
N
*
(
或
N
+
)
Z
Q
R
必备知识预案自诊
4
知识梳理
考点自测
2
.
集合间的基本关系
A
⊆
B
(
或
B
⊇
A
)
A
⫋
B
(
或
B
⫌
A
)
A=B
必备知识预案自诊
5
知识梳理
考点自测
3
.
集合的运算
{
x|x
∈
A
或
x
∈
B
}
{
x|x
∈
A
,
且
x
∈
B
}
{
x|x
∈
U
,
且
x
∉
A
}
必备知识预案自诊
6
知识梳理
考点自测
1
.
并集的性质
:
A
∪
⌀
=A
;
A
∪
A=A
;
A
∪
B=B
∪
A
;
A
∪
B=A
⇔
B
⊆
A.
2
.
交集的性质
:
A
∩
⌀
=
⌀
;
A
∩
A=A
;
A
∩
B=B
∩
A
;
A
∩
B=A
⇔
A
⊆
B.
3
.
补集的性质
:
A
∩(
∁
U
A
)
=
⌀
;
A
∪
(
∁
U
A
)
=U
;
∁
U
(
∁
U
A
)
=A
;
∁
U
(
A
∪
B
)
=
(
∁
U
A
)∩(
∁
U
B
);
∁
U
(
A
∩
B
)
=
(
∁
U
A
)
∪
(
∁
U
B
)
.
4
.
若集合
A
中含有
n
个元素
,
则它的子集个数为
2
n
,
真子集的个数为
2
n
-
1,
非空真子集的个数为
2
n
-
2
.
必备知识预案自诊
7
知识梳理
考点自测
1
.
判断下列结论是否正确
,
正确的画
“
√
”,
错误的画
“
×
”
.
(1)
集合
{
x
2
+x
,0}
中的实数
x
可取任意值
.
(
)
(2){
x|y=x
2
+
1}
=
{
y|y
=x
2
+
1}
=
{(
x
,
y
)
|y
=x
2
+
1}
.
(
)
(3)
A
⊆
B
⇔
A
∩
B=A
⇔
A
∪
B=B
,(
A
∩
B
)
⊆
(
A
∪
B
)
.
(
)
(4)
若
A
∩
B=A
∩
C
,
则
B=C.
(
)
(5)
直线
y=x+
3
与
y=-
2
x+
6
的交点组成的集合是
{1,4}
.
(
)
×
√
×
×
×
必备知识预案自诊
8
知识梳理
考点自测
2
.
(2016
全国
Ⅱ
,
文
1)
已知集合
A=
{1,2,3},
B=
{
x|x
2
<
9},
则
A
∩
B=
(
)
A.{
-
2,
-
1,0,1,2,3} B.{
-
2,
-
1,0,1,2}
C.{1,2,3} D.{1,2}
解析
:
由
x
2
<
9,
得
-
3
0},
则
(
)
5
.
设集合
A=
{
x|
(
x+
1)·(
x-
2)
<
0},
集合
B=
{
x|
1
4
.
故实数
a
的取值范围是
(4,
+∞
)
.
关键能力学案突破
14
考点一
考点二
考点三
学科素养微专题
思考
判定集合间的基本关系有哪些方法
?
解决集合间基本关系的常用技巧有哪些
?
解题心得
1
.
判定集合间的基本关系的方法有两种
.
一是化简集合
,
从表达式中寻找集合间的关系
;
二是用列举法
(
或图示法等
)
表示各个集合
,
从元素
(
或图形
)
中寻找集合间的关系
.
2
.
解决集合间基本关系的常用技巧有
:(1)
若给定的集合是不等式的解集
,
则结合数轴求解
;(2)
若给定的集合是点集
,
则用数形结合法求解
;(3)
若给定的集合是抽象集合
,
则用
Venn
图求解
.
关键能力学案突破
15
考点一
考点二
考点三
学科素养微专题
对点训练
2
已知集合
A=
{
x|x
<-
3
或
x>
7},
B=
{
x|x
<
2
m-
1},
若
B
⊆
A
,
则实数
m
的取值范围是
.
答案
:
(
-∞
,
-
1]
解析
:
由题意知
2
m-
1
≤
-
3,
m
≤
-
1,
所以
m
的取值范围是
(
-∞
,
-
1]
.
关键能力学案突破
16
考点一
考点二
考点三
学科素养微专题
变式发散
1
将本题中的
B
改为
B=
{
x|m+
1
≤
x
≤
2
m-
1},
其余不变
,
该如何求解
?
答案
:
(
-∞
,2)
∪
(6,
+∞
)
解析
:
当
B=
⌀
时
,
有
m+
1
>
2
m-
1,
则
m<
2
.
解得
m>
6
.
综上可知
,
m
的取值范围是
(
-∞
,2)
∪
(6,
+∞
)
.
关键能力学案突破
17
考点一
考点二
考点三
学科素养微专题
变式发散
2
将本题中的
A
改为
A=
{
x|-
3
≤
x
≤
7},
B
改为
B=
{
x|m+
1
≤
x
≤
2
m-
1},
其余不变
,
又该如何求解
?
答案
:
(
-∞
,4]
关键能力学案突破
18
考点一
考点二
考点三
学科素养微专题
集合的基本运算
(
多考向
)
考向
1
求集合的交集、并集、补集
例
3
(1)(2017
天津
,
文
1)
设集合
A=
{1,2,6},
B=
{2,4},
C=
{1,2,3,4},
则
(
A
∪
B
)∩
C=
(
)
A.{2} B.{1,2,4}
C.{1,2,4,6} D.{1,2,3,4,6}
(2)(2017
河南濮阳一模
,
文
1)
已知全集
U=
{1,2,3,4,5,6},
M=
{2,3,5},
N=
{4,5},
则
∁
U
(
M
∪
N
)
=
(
)
A.{2,3,4,5} B.{5}
C.{1,6} D.{1,2,3,4,6}
B
C
解析
:
(1)
∵
A=
{1,2,6},
B=
{2,4},
C=
{1,2,3,4},
∴
A
∪
B=
{1,2,4,6},(
A
∪
B
)∩
C=
{1,2,4}
.
故选
B
.
(2)
∵
全集
U=
{1,2,3,4,5,6},
M=
{2,3,5},
N=
{4,5},
∴
M
∪
N=
{2,3,4,5},
∴
∁
U
(
M
∪
N
)
=
{1,6}
.
故选
C
.
关键能力学案突破
19
考点一
考点二
考点三
学科素养微专题
思考
集合基本运算的求解策略是什么
?
解题心得
1
.
求解思路
:
一般是先化简集合
,
再由交集、并集、补集的定义求解
.
2
.
求解原则
:
一般是先算括号里面的
,
然后再按运算顺序求解
.
3
.
求解思想
:
注重数形结合思想的运用
,
利用好数轴、
Venn
图等
.
关键能力学案突破
20
考点一
考点二
考点三
学科素养微专题
对点训练
3
(1)(2017
山西临汾二模
,
文
1)
已知集合
A=
{0,1,2,3},
B=
{
x|
ln
x>
0},
则
A
∩
B=
(
)
A.{0,1,2,3} B.{1,2,3} C.{2,3} D.{3}
(2)(2017
湖南株洲模拟
,
文
1)
已知全集
U=
{0,1,2,3,4,5},
集合
A=
{2,4},
B=
{
y|y
=
(
x-
1),
x
∈
A
},
则集合
(
∁
U
A
)∩(
∁
U
B
)
=
(
)
A.{0,4,5,2} B.{0,4,5} C.{2,4,5} D.{1,3,5}
C
D
解析
:
(1)
因为
A=
{0,1,2,3},
B=
{
x|
ln
x>
0}
=
{
x|x
>
1},
所以
A
∩
B=
{2,3},
故选
C
.
(2)
由题意知
B=
{0,2},
所以
∁
U
A=
{0,1,3,5},
∁
U
B=
{1,3,4,5}
.
故
(
∁
U
A
)∩(
∁
U
B
)
=
{1,3,5}
.
关键能力学案突破
21
考点一
考点二
考点三
学科素养微专题
考向
2
已知集合运算求参数
(2)
已知集合
M=
{
x|-
1
≤
x<
2},
N=
{
y|y
-
1
B
D
关键能力学案突破
22
考点一
考点二
考点三
学科素养微专题
思考
若集合的元素中含有参数
,
求这些参数有哪些技巧
?
解题心得
一般来讲
,
若集合中的元素是离散的
,
则用
Venn
图表示
,
根据
Venn
图得到关于参数的一个或多个方程
,
求出参数后要验证是否与集合元素的互异性矛盾
;
若集合中的元素是连续的
,
则用数轴表示
,
根据数轴得到关于参数的不等式
,
解之得到参数的取值范围
,
此时要注意端点的取舍
.
关键能力学案突破
23
考点一
考点二
考点三
学科素养微专题
对点训练
4
(1)(2017
河北衡水金卷一
,
文
3)
已知集合
M=
{
x|-
1
≤
x
≤
2},
N=
{
x|
1
-
3
a
0
时
,
由
B
⊆
A
,
得
B=
{
-
1,
-
2},
m=
(
-
1)
×
(
-
2)
=
2
.
经检验知
m=
1
和
m=
2
符合条件
.
∴
m=
1
或
2
.
关键能力学案突破
25
考点一
考点二
考点三
学科素养微专题
解答集合问题时应注意五点
:
(1)
注意集合中元素的性质
——
互异性的应用
,
解答时注意检验
.
(2)
注意描述法给出的集合的元素的特征
.
如
{
y|y
=
2
x
},{
x|y=
2
x
},{(
x
,
y
)
|y=
2
x
}
表示不同的集合
.
(3)
注意
⌀
的特殊性
.
在利用
A
⊆
B
解题时
,
应对
A
是否为
⌀
进行讨论
.
(4)
注意数形结合思想的应用
.
在进行集合运算时要尽可能借助
Venn
图和数轴使抽象问题直观化
.
一般地
,
当集合元素离散时
,
用
Venn
图表示
;
当元素连续时
,
用数轴表示
,
同时注意端点的取舍
.
(5)
注意补集思想的应用
.
在解决
A
∩
B
≠
⌀
时
,
可以利用补集思想
,
先研究
A
∩
B=
⌀
的情况
,
然后取补集
.
关键能力学案突破
26
考点一
考点二
考点三
学科素养微专题
创新能力训练
——
新定义型集合问题
关键能力学案突破
27
考点一
考点二
考点三
学科素养微专题
(3)
已知数集
A=
{
a
1
,
a
2
,
…
,
a
n
}(1
≤
a
1
查看更多