2020年高考数学(理)二轮复习讲练测 专题08 不等式（讲）（原卷版）

2020年高考数学(理)二轮复习讲练测 专题08 不等式（讲）（原卷版）

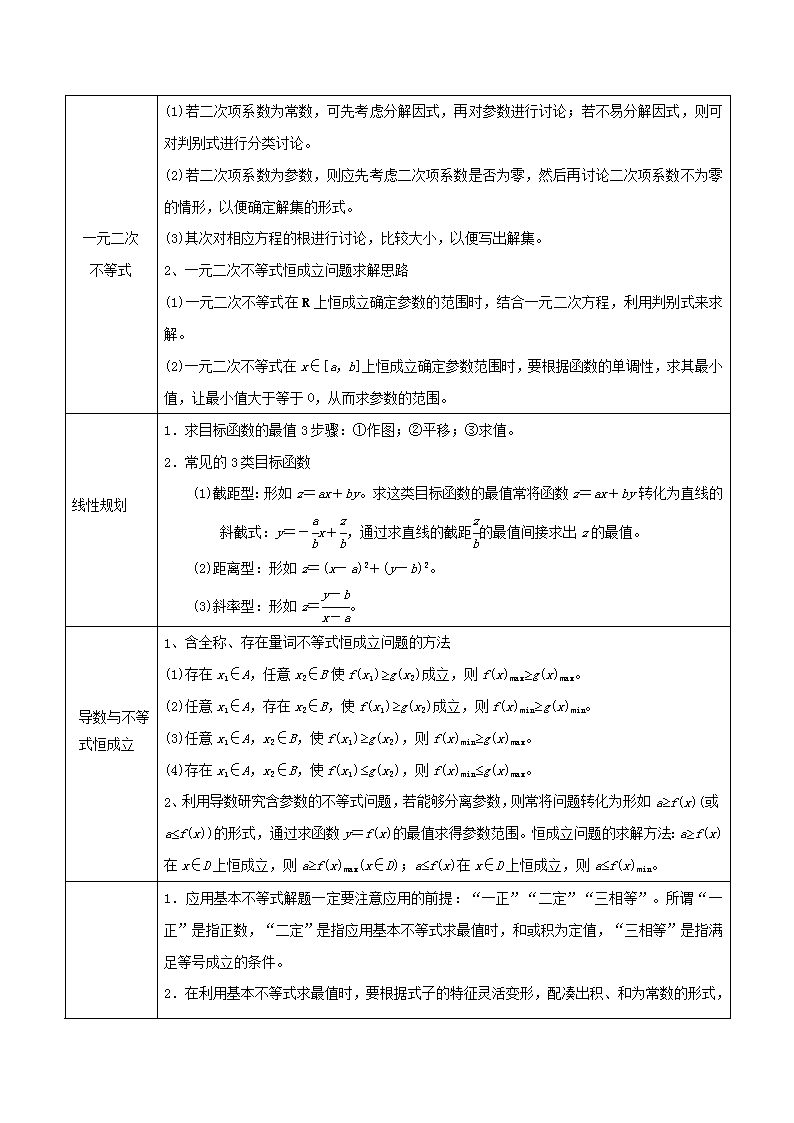
专题08 不等式(讲)‎ ‎1．【2019年高考全国II卷理数】若a>b，则( )‎ A．ln(a−b)>0 B．3a<3b C．a3−b3>0 D．│a│>│b│‎ ‎2．【2019年高考天津卷理数】设变量满足约束条件，则目标函数的最大值为( )‎ A．2 B．3 ‎ C．5 D．6‎ ‎3．【2019年高考天津卷理数】设，则的最小值为__________．‎ ‎4【2019年高考天津卷理数】设，则“”是“”的( )‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 一、考向分析： ‎ ‎ 不等式 一元二次不等式 导数与不等式恒成立 数列与不等式证明 基本不等式 线性规划 ‎ 二、考向讲解 考查内容 ‎ 解 题 技 巧 ‎ ‎1、含有参数的不等式的求解，往往需要比较(相应方程)根的大小，对参数进行分类讨论 一元二次 不等式 ‎(1)若二次项系数为常数，可先考虑分解因式，再对参数进行讨论；若不易分解因式，则可对判别式进行分类讨论。‎ ‎(2)若二次项系数为参数，则应先考虑二次项系数是否为零，然后再讨论二次项系数不为零的情形，以便确定解集的形式。‎ ‎(3)其次对相应方程的根进行讨论，比较大小，以便写出解集。‎ ‎2、一元二次不等式恒成立问题求解思路 ‎(1)一元二次不等式在R上恒成立确定参数的范围时，结合一元二次方程，利用判别式来求解。‎ ‎(2)一元二次不等式在x∈[a，b]上恒成立确定参数范围时，要根据函数的单调性，求其最小值，让最小值大于等于0，从而求参数的范围。‎ 线性规划 ‎1．求目标函数的最值3步骤：①作图；②平移；③求值。‎ ‎2．常见的3类目标函数 ‎(1)截距型：形如z＝ax＋by。求这类目标函数的最值常将函数z＝ax＋by转化为直线的斜截式：y＝－x＋，通过求直线的截距的最值间接求出z的最值。‎ ‎(2)距离型：形如z＝(x－a)2＋(y－b)2。‎ ‎(3)斜率型：形如z＝。‎ 导数与不等式恒成立 ‎1、含全称、存在量词不等式恒成立问题的方法 ‎(1)存在x1∈A，任意x2∈B使f(x1)≥g(x2)成立，则f(x)max≥g(x)max。‎ ‎(2)任意x1∈A，存在x2∈B，使f(x1)≥g(x2)成立，则f(x)min≥g(x)min。‎ ‎(3)任意x1∈A，x2∈B，使f(x1)≥g(x2)，则f(x)min≥g(x)max。‎ ‎(4)存在x1∈A，x2∈B，使f(x1)≤g(x2)，则f(x)min≤g(x)max。‎ ‎2、利用导数研究含参数的不等式问题，若能够分离参数，则常将问题转化为形如a≥f(x)(或a≤f(x))的形式，通过求函数y＝f(x)的最值求得参数范围。恒成立问题的求解方法：a≥f(x)在x∈D上恒成立，则a≥f(x)max(x∈D)；a≤f(x)在x∈D上恒成立，则a≤f(x)min。‎ ‎1．应用基本不等式解题一定要注意应用的前提：“一正”“二定”“三相等”。所谓“一正”是指正数，“二定”是指应用基本不等式求最值时，和或积为定值，“三相等”是指满足等号成立的条件。‎ 基本不 等式 ‎2．在利用基本不等式求最值时，要根据式子的特征灵活变形，配凑出积、和为常数的形式，然后再利用基本不等式。‎ ‎3、条件最值的求解通常有三种方法：一是消元法，即根据条件建立两个量之间的函数关系，然后代入代数式转化为函数的最值求解；二是将条件灵活变形，利用常数代换的方法构造和或积为常数的式子，然后利用基本不等式求解最值；三是对条件使用基本不等式，建立所求目标函数的不等式求解。‎ ‎4、基本不等式的应用非常广泛，它可以和数学的其他知识交汇考查，解决这类问题的策略是：‎ ‎(1)先根据所交汇的知识进行变形，通过换元、配凑、巧换“‎1”‎等手段把最值问题转化为用基本不等式求解，这是难点。‎ ‎(2)用基本不等式求最值，要有用基本不等式求最值的意识。‎ ‎(3)检验。检验等号是否成立，完成后续问题。‎ 数列与不 等式证明 ‎1．两平面向量共线的充要条件有两种形式 ‎①若a＝(x1，y1)，b＝(x2，y2)，则a∥b的充要条件是x1y2－x2y1＝0；②a∥b(b≠0)⇔a＝λb。‎ ‎2．向量共线的坐标表示既可以判定两向量平行，也可以由平行求参数。当两向量的坐标均非零时，也可以利用坐标对应成比例来求解。‎ 考查一元二次不等式解法：‎ ‎【例1】已知不等式x2－2x－3<0的解集为A，不等式x2＋x－6<0的解集为B，不等式x2＋ax＋b<0的解集为A∩B，则a＋b＝(　　)‎ A．－3 B．1 C．－1 D．3‎ ‎【例2】　解关于x的不等式ax2－(a＋1)x＋1<0(a∈R)。‎ 考查一元二次不等式恒成立：‎ ‎【典例1】已知定义在R上的奇函数f(x)满足：当x≥0时，f(x)＝x3，若不等式f(－4t)>f(‎2m＋mt2)对任意实数t恒成立，则实数m的取值范围是( )‎ A．(－∞，－) B．(－，0) C．(－∞，0)∪(，＋∞) D．(－∞，－)∪(，＋∞)‎ ‎【典例2】设函数f(x)＝mx2－mx－1。若对于x∈[1,3]，f(x)<－m＋5恒成立，求m的取值范围。‎ 考查基本不等式：‎ ‎【例1】已知a，b∈R，且a–3b+6=0，则2a+的最小值为__________．‎ ‎【例2】若正数满足，则的最小值为( )‎ A． B． C． D．3‎ ‎【例3】已知x< ，求f(x)＝4x－2＋的最大值。‎ 考查线性规划：‎ ‎【例1】设变量满足约束条件则目标函数的最大值为( )‎ ‎(A)6 (B)19 (C)21 (D)45‎ ‎【例2】某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为( )‎ A．12万元 B．16万元 C．17万元 D．18万元 考查数列与不等式：‎ ‎【例1】已知正项数列{an}的前n项和为Sn，且Sn，an，成等差数列。‎ ‎(1)求数列{an}的通项公式，(2)若bn＝log2an＋2，设数列的前n项和为Tn，证明≤Tn<1。‎ 考查导数与不等式：‎ ‎【例1】已知函数，证明：当时，．‎ ‎【例2】已知函数，若，证明：当时，；当时，；‎ 不等式恒成立问题 分离参数求参数取值范围 ‎【例1】已知函数f(x)＝ex＋ax2－e2x。若x>0时，总有f(x)>－e2x，求实数a的取值范围。‎ 小结：利用导数研究含参数的不等式问题，若能够分离参数，则常将问题转化为形如a≥f(x)(或a≤f(x))的形式，通过求函数y＝f(x)的最值求得参数范围。恒成立问题的求解方法：a≥f(x)在x∈D上恒成立，则a≥f(x)max(x∈D)；a≤f(x)在x∈D上恒成立，则a≤f(x)min。‎ 转化法求参数范围 ‎【例2】设函数f(x)＝a2lnx＋ax(a≠0)，g(x)＝2tdt，F(x)＝g(x)－f(x)。‎ ‎(1)试讨论F(x)的单调性。(2)当a>0时，－e2≤F(x)≤1－e在x∈[1，e]恒成立，求实数a的取值。‎ 小结：破解此类题需“一形一分类”，“一形”是指会结合函数的图象，对函数进行求导，然后判断其极值，从而得到含有参数的方程组，解方程组，即可求出参数的值；“一分类”是指对不等式恒成立问题，常需对参数进行分类讨论，求出参数的取值范围。‎ 不等式能成立问题 含参数的能成立(存在型)问题 ‎【例1】已知函数f(x)＝x3－ax2＋10。‎ ‎(1)当a＝1时，求曲线y＝f(x)在点(2，f(2))处的切线方程。‎ ‎(2)在区间[1,2]内至少存在一个实数x，使得f(x)<0成立，求实数a的取值范围。‎ 小结：含参数的能成立(存在型)问题的解题方法 ‎(1)a≥f(x)在x∈D上能成立，则a≥f(x)min； (2)a≤f(x)在x∈D上能成立，则a≤f(x)max。‎ 含有全称量词与存在量词的不等式问题 ‎【例2】已知函数f(x)＝lnx－mx(m∈R)，g(x)＝x－(a>0)。‎ ‎(1)求函数f(x)的单调区间。‎ ‎(2)若m＝，对∀x1，x2∈[2,2e2]都有g(x1)≥f(x2)成立，求实数a的取值范围。‎ 小结：含全称、存在量词不等式恒成立问题的方法 ‎1．存在x1∈A，任意x2∈B使f(x1)≥g(x2)成立，则f(x)max≥g(x)max。‎ ‎2．任意x1∈A，存在x2∈B，使f(x1)≥g(x2)成立，则f(x)min≥g(x)min。‎ ‎3．任意x1∈A，x2∈B，使f(x1)≥g(x2)，则f(x)min≥g(x)max。‎ ‎4．存在x1∈A，x2∈B，使f(x1)≤g(x2)，则f(x)min≤g(x)max。‎