2018届二轮复习立体几何中的翻折问题的分析与解学案

2018届二轮复习立体几何中的翻折问题的分析与解学案

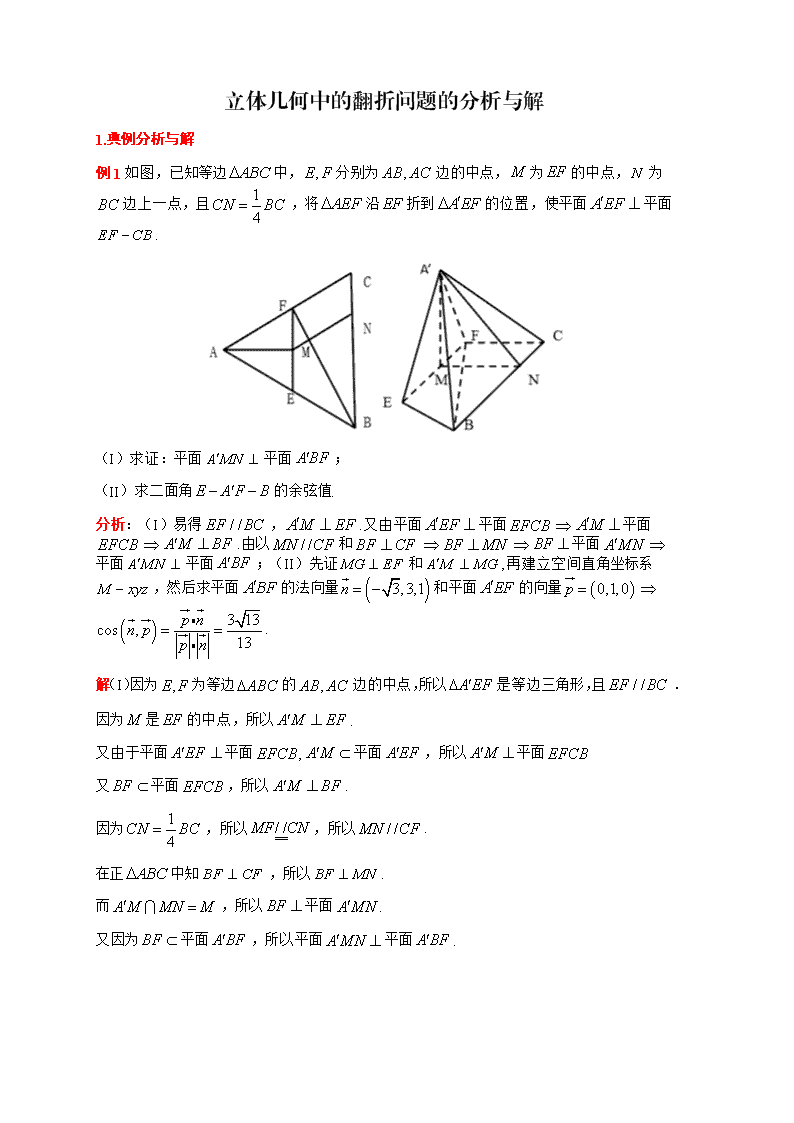
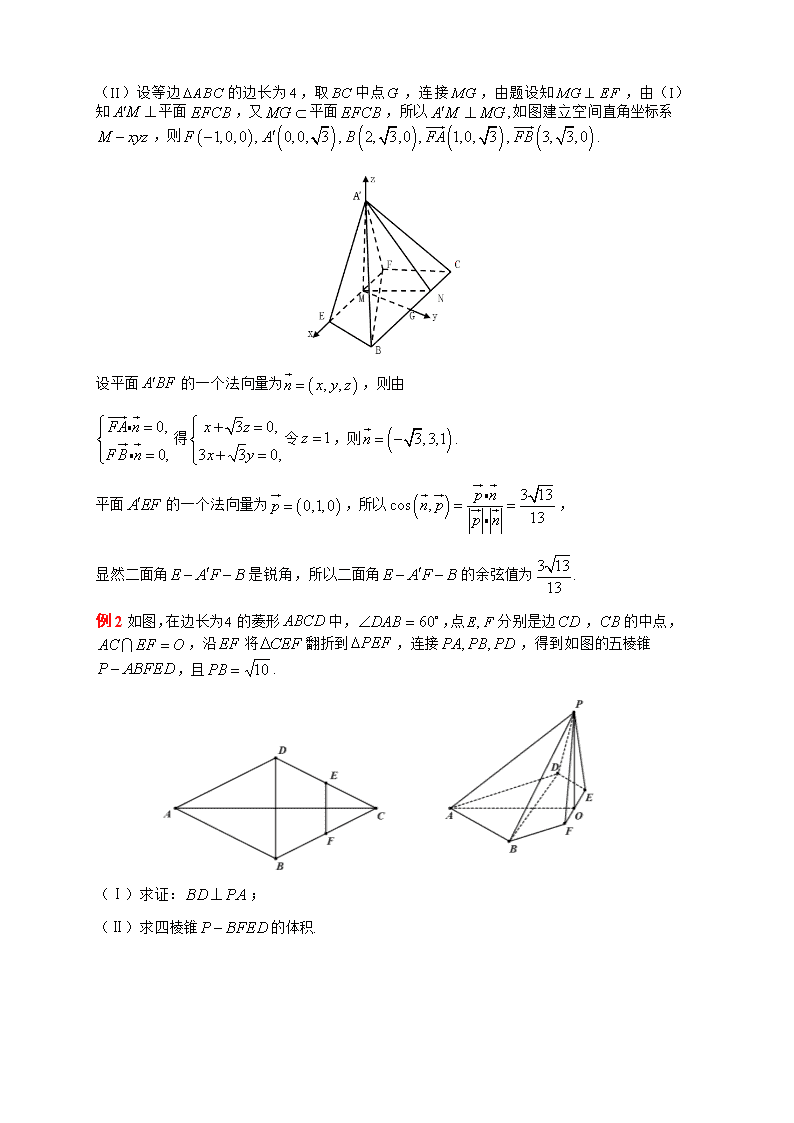
立体几何中的翻折问题的分析与解 ‎1.典例分析与解 例1如图，已知等边中，分别为边的中点，为的中点，为边上一点，且，将沿折到的位置，使平面平面.‎ ‎（I）求证：平面平面；‎ ‎（II）求二面角的余弦值.‎ 分析：（I）易得，.又由平面平面平面.由以和平面平面平面；（II）先证和,再建立空间直角坐标系，然后求平面的法向量和平面的向量.‎ 解（I）因为为等边的边的中点，所以是等边三角形，且．‎ 因为是的中点，所以.‎ 又由于平面平面,平面，所以平面 又平面，所以.‎ 因为，所以，所以.‎ 在正中知，所以.‎ 而，所以平面.‎ 又因为平面，所以平面平面.‎ ‎（II）设等边的边长为4，取中点，连接，由题设知，由（I）知平面，又平面，所以,如图建立空间直角坐标系，则,,,,.‎ 设平面的一个法向量为，则由 得令，则.‎ 平面的一个法向量为，所以，‎ 显然二面角是锐角，所以二面角的余弦值为.‎ 例2如图，在边长为的菱形中，，点分别是边，的中点，，沿将翻折到，连接，得到如图的五棱锥，且.‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求四棱锥的体积.‎ 分析（Ⅰ）由题证明，则平面，可得；（Ⅱ）由勾股定理可得，又，可知为四棱锥的高，则四棱锥的体积.‎ 解（Ⅰ）证明：∵点分别是边的中点，‎ ‎∴.‎ ‎∵菱形的对角线互相垂直，∴.∴.‎ ‎∴，‎ ‎∵平面，平面，，‎ ‎∴平面，∴平面，∴.‎ ‎（Ⅱ）解：设。连接，∵，‎ ‎∴为等边三角形，∴，‎ 在中，，‎ 在中，，∴.‎ ‎∵，，平面，平面，‎ ‎∴平面，‎ 梯形的面积，‎ ‎∴四棱锥的体积.‎ ‎2.小试牛刀 练习1已知平行四边形，，，，为的中点，把三角形沿折起至位置，使得，是线段的中点.‎ ‎（1）求证：面；‎ ‎（2）求证：面面；‎ ‎（3）求四棱锥的体积.‎ 分析（1）取的中点，连接、，通过证明，利用直线与平面平行的判定定理证明面；（2）取的中点，连接、，通过证明面，然后通过平面与平面垂直的判定定理证明面面；（3）利用（2）的结果，直接求解几何体的体积即可．‎ 解（1）证明：取的中点，连接，为中点，‎ ‎，且，‎ 为平行四边形边的中点，‎ ‎，且，‎ ‎，且，‎ 四边形是平行四边形，，‎ 平面，平面，‎ 平面．‎ ‎（2）取的中点，连接，‎ ‎，，，为的中点，‎ 为等边三角形，即折叠后也为等边三角形，‎ ‎，且，‎ 在中，，，，‎ 根据余弦定理，可得，在中，，，，‎ ‎，即，‎ 又，所以面，‎ 又面，面面 ‎（3）由第（2）问知面，‎ ‎.‎ 练习2如图，在正方形中，点分别是的中点，将分别沿、折起，使两点重合于.‎ ‎(Ⅰ)求证：平面⊥平面；‎ ‎(Ⅱ)求四棱锥的体积.‎ 分析（Ⅰ）由折叠前四边形形为正方形，可得折叠后，得平面，得平面平面；（Ⅱ）作棱锥的高在中，由，得,很容易得出四边形的面积，即可得到四棱锥的体积.‎ 解 (Ⅰ)证明：连接交于，连接.在正方形中，点是的中点，点是的中点，所以，所以，因此，所以在等腰中，是的中点，且.因此在等腰中，‎ ‎，从而平面.又平面，所以平面⊥平面.即平面平面.‎ ‎（Ⅱ）由（Ⅰ）的证明可知平面⊥平面,易知，，由于，所以.作于，则平面.在中，由，得,又四边形的面积，所以，四棱锥的体积.‎