- 2021-06-21 发布 |
- 37.5 KB |
- 33页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习(文)高考22题各个击破(4)课件(全国通用)
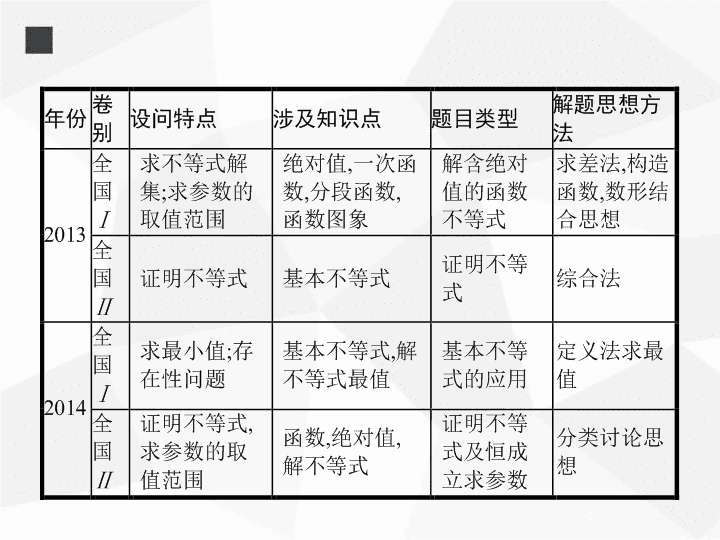
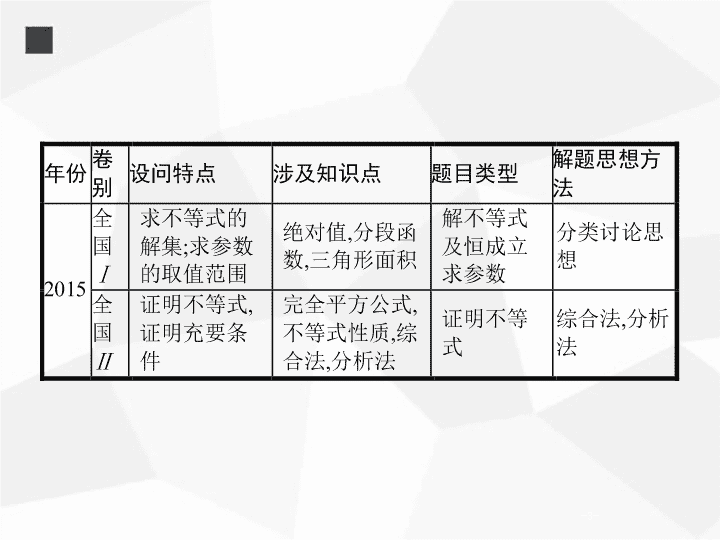
9.2 不等式选讲 ( 选修 4—5) - 2 - - 3 - - 4 - - 5 - - 6 - 1 . 绝对值三角不等式 (1) 定理 1: 若 a , b 是实数 , 则 |a+b| ≤ |a|+|b| , 当且仅当 ab ≥ 0 时 , 等号成立 ; (2) 性质 : |a|-|b| ≤ |a±b| ≤ |a|+|b| ; (3) 定理 2: 若 a , b , c 是实数 , 则 |a-c| ≤ |a-b|+|b-c| , 当且仅当 ( a-b )( b-c ) ≥ 0 时 , 等号成立 . - 7 - 2 . 绝对值不等式的解法 (1) 含绝对值的不等式 |x|a ( a> 0) 的解法 : ① |x|a ⇔ x>a 或 x<-a. (2) |ax+b| ≤ c ( c> 0) 和 |ax+b| ≥ c ( c> 0) 型不等式的解法 : ① |ax+b| ≤ c ⇔ -c ≤ ax+b ≤ c ; ② |ax+b| ≥ c ⇔ ax+b ≥ c 或 ax+b ≤ -c. (3) |x-a|+|x-b| ≥ c ( c> 0) 和 |x-a|+|x-b| ≤ c ( c> 0) 型不等式的解法 : ① 利用绝对值不等式的几何意义求解 , 体现了数形结合的思想 ; ② 利用 “ 零点分段法 ” 求解 , 体现了分类讨论的思想 . ③ 通过构造函数 , 利用函数的图象求解 , 体现了函数与方程的思想 . - 8 - 3 . 基本不等式 定理 1: 设 a , b ∈ R , 则 a 2 +b 2 ≥ 2 ab , 当且仅当 a=b 时 , 等号成立 . - 9 - 4 . 不等式的证明方法 证明不等式常用的方法有比较法、综合法、分析法、反证法、放缩法等 . (1) 比较法 : 求差比较法 , 求商比较法 . ① 求差比较法 : 由于 a>b ⇔ a-b> 0, ab , 只要证明 a-b> 0 即可 . (2) 分析法 : 从待证不等式出发 , 逐步寻求使它成立的充分条件 , 直到将待证不等式归结为一个已成立的不等式 ( 已知条件、定理等 ) . (3) 综合法 : 从已知条件出发 , 利用不等式的有关性质或定理 , 经过推理论证 , 推导出所要证明的不等式成立 , 即 “ 由因寻果 ” 的方法 , 这种证明不等式的方法称为综合法 . - 10 - 5 . 柯西 不等式 - 11 - 考向一 考向二 考向三 考向四 解绝对值不等式、求参数范围 解题策略一 分离参数法求参数范围 例 1 (2017 全国 Ⅲ , 文 23 ) 已知函数 f ( x ) =|x+ 1 |-|x- 2 |. (1) 求不等式 f ( x ) ≥ 1 的解集 ; (2) 若不等式 f ( x ) ≥ x 2 -x+m 的解集非空 , 求 m 的取值范围 . 当 x<- 1 时 , f ( x ) ≥ 1 无解 ; 当 - 1 ≤ x ≤ 2 时 , 由 f ( x ) ≥ 1, 得 2 x- 1 ≥ 1, 解得 1 ≤ x ≤ 2; 当 x> 2 时 , 由 f ( x ) ≥ 1 解得 x> 2 . 所以 f ( x ) ≥ 1 的解集为 { x|x ≥ 1} . - 12 - 考向一 考向二 考向三 考向四 (2) 由 f ( x ) ≥ x 2 -x+m 得 m ≤ |x+ 1 |-|x- 2 |-x 2 +x . 解题心得 1 . 解含有两个以上绝对值符号的不等式 , 一般解法是零点分段法 . 即令各个绝对值式子等于 0, 求出各自零点 , 把零点在数轴上从小到大排列 , 然后按零点分数轴形成的各区间去绝对值 , 进而将绝对值不等式转化为常规不等式 . 2 . 在不等式恒成立的情况下 , 求参数的取值范围 , 可以采取分离参数 , 通过求对应函数最值的方法获得 . - 13 - 考向一 考向二 考向三 考向四 对点训练 1 (2017 山西太原二模 , 文 23 ) 已知函数 f ( x ) =|x+m|+| 2 x- 1 | ( m> 0) . (1) 当 m= 1 时 , 解不等式 f ( x ) ≥ 3; (2) 当 x ∈ [ m ,2 m 2 ] 时 , 不等式 f ( x ) ≤ |x+ 1 | 恒成立 , 求实数 m 的取值范围 . 解 (1) m= 1 时 , f ( x ) =|x+ 1 |+| 2 x- 1 | , ∴ f ( x ) ≥ 3, 解得 x ≤ - 1 或 x ≥ 1 . - 14 - 考向一 考向二 考向三 考向四 - 15 - 考向一 考向二 考向三 考向四 解题策略二 求函数最值构造不等式求参数范围 例 2 (2017 全国 Ⅰ , 文 23 ) 已知函数 f ( x ) =-x 2 +ax+ 4, g ( x ) =|x+ 1 |+|x- 1 |. (1) 当 a= 1 时 , 求不等式 f ( x ) ≥ g ( x ) 的解集 ; (2) 若不等式 f ( x ) ≥ g ( x ) 的解集包含 [ - 1,1], 求 a 的取值范围 . 解 (1) 当 a= 1 时 , 不等式 f ( x ) ≥ g ( x ) 等价于 x 2 -x+|x+ 1 |+|x- 1 |- 4 ≤ 0 . ① 当 x<- 1 时 , ① 式化为 x 2 - 3 x- 4 ≤ 0, 无解 ; 当 - 1 ≤ x ≤ 1 时 , ① 式化为 x 2 -x- 2 ≤ 0, 从而 - 1 ≤ x ≤ 1; - 16 - 考向一 考向二 考向三 考向四 (2) 当 x ∈ [ - 1,1] 时 , g ( x ) = 2 . 所以 f ( x ) ≥ g ( x ) 的解集包含 [ - 1,1], 等价于当 x ∈ [ - 1,1] 时 f ( x ) ≥ 2 . 又 f ( x ) 在 [ - 1,1] 的最小值必为 f ( - 1) 与 f (1) 之一 , 所以 f ( - 1) ≥ 2 且 f (1) ≥ 2, 得 - 1 ≤ a ≤ 1 . 所以 a 的取值范围为 [ - 1,1] . 解题心得 1 . 对于求参数范围问题 , 可将已知条件进行等价转化 , 得到含有参数的不等式恒成立 , 此时通过求函数的最值得到关于参数的不等式 , 解不等式得参数范围 . 2 . 解答此类问题应熟记以下转化 : f ( x ) >a 恒成立 ⇔ f ( x ) min >a ; f ( x ) a 有解 ⇔ f ( x ) max >a ; f ( x ) a 无解 ⇔ f ( x ) max ≤ a ; f ( x ) 0, b> 0, a 3 +b 3 = 2 . 证明 : (1)( a+b )( a 5 +b 5 ) ≥ 4; (2) a+b ≤ 2 . 解 (1)( a+b )( a 5 +b 5 ) =a 6 +ab 5 +a 5 b+b 6 = ( a 3 +b 3 ) 2 - 2 a 3 b 3 +ab ( a 4 +b 4 ) = 4 +ab ( a 2 -b 2 ) 2 ≥ 4 . (2) 因为 ( a+b ) 3 =a 3 + 3 a 2 b+ 3 ab 2 +b 3 所以 ( a+b ) 3 ≤ 8, 因此 a+b ≤ 2 . - 20 - 考向一 考向二 考向三 考向四 解题心得 不等式证明的常用方法是 : 比较法、综合法与分析法 . 其中运用综合法证明不等式时 , 主要是运用基本不等式证明 , 与绝对值有关的不等式证明常用绝对值三角不等式 . 证明过程中一方面要注意不等式成立的条件 , 另一方面要善于对式子进行恰当的转化、变形 . - 21 - 考向一 考向二 考向三 考向四 对点训练 3 设 a , b , c , d 均为正数 , 且 a+b=c+d , 证明 : - 22 - 考向一 考向二 考向三 考向四 (2) ① 若 |a-b|<|c-d| , 则 ( a-b ) 2 < ( c-d ) 2 , 即 ( a+b ) 2 - 4 ab< ( c+d ) 2 - 4 cd. 因为 a+b=c+d , 所以 ab>cd. 因为 a+b=c+d , 所以 ab>cd. 于是 ( a-b ) 2 = ( a+b ) 2 - 4 ab< ( c+d ) 2 - 4 cd= ( c-d ) 2 . 因此 |a-b|<|c-d|. - 23 - 考向一 考向二 考向三 考向四 求最值 解题策略一 利用基本不等式求最值 (1) 求 a 3 +b 3 的最小值 . (2) 是否存在 a , b , 使得 2 a+ 3 b= 6? 并说明理由 . - 24 - 考向一 考向二 考向三 考向四 解题心得 若题设条件有 ( 或者经过化简题设条件得到 ) 两个正数和或两个正数积为定值 , 则可利用基本不等式求两个正数积的最大值或两个正数和的最小值 . - 25 - 考向一 考向二 考向三 考向四 对点训练 4 (2017 辽宁大连一模 , 文 23 ) 已知 a> 0, b> 0, 函数 f ( x ) =|x+a|+| 2 x-b| 的最小值为 1 . (1) 求证 :2 a+b= 2; (2) 若 a+ 2 b ≥ tab 恒成立 , 求实数 t 的最大值 . - 26 - 考向一 考向二 考向三 考向四 - 27 - 考向一 考向二 考向三 考向四 解题策略二 利用柯西不等式求最值 例 5 (2017 四川成都二诊 , 文 23 )(1) 已知函数 f ( x ) = 4 -|x|-|x- 3 |. 求 不等式 ≥ 0 的解集 . 综上所述 , 不等式的解集为 [ - 2,2 ] . - 28 - 考向一 考向二 考向三 考向四 解题心得 利用柯西不等式求最值时 , 一定要满足柯西不等式的形式 . - 29 - 考向一 考向二 考向三 考向四 对点训练 5 (2017 河南洛阳一模 , 文 23 )(1) 已知关于 x 的不等式 |x+ 3 |+|x+m| ≥ 2 m 的解集为 R . 求 m 的最大值 . (2) 已知 a> 0, b> 0, c> 0, 且 a+b+c= 1, 求 2 a 2 + 3 b 2 + 4 c 2 的最小值及此时 a , b , c 的值 . 解 (1) ∵ |x+ 3 |+|x+m| ≥ | ( x+ 3) - ( x+m ) |=|m- 3 |. 当 - 3 ≤ x ≤ -m 或 -m ≤ x ≤ - 3 时取等号 , 令 |m- 3 | ≥ 2 m , ∴ m- 3 ≥ 2 m 或 m- 3 ≤ - 2 m. 解得 m ≤ 1, ∴ m 的最大值为 1 . - 30 - 考向一 考向二 考向三 考向四 (2) ∵ a+b+c= 1, 由柯西不等式 得 当且仅当 2 a= 3 b= 4 c , 且 a+b+c= 1 时等号成立 . - 31 - 考向一 考向二 考向三 考向四 绝对值三角不等式的 应用 (1) 证明 f ( x ) ≥ 2; (2) 若 f (3) < 5, 求 a 的取值范围 . - 32 - 考向一 考向二 考向三 考向四 解题心得 绝对值三角不等式、基本不等式在解决多变量代数式的最值问题中有着重要的应用 , 无论运用绝对值三角不等式还是运用基本不等式时应注意等号成立的条件 . - 33 - 考向一 考向二 考向三 考向四 对点训练 6 (2017 湖南长沙一模 , 文 23 ) 已知 f ( x ) =|x-a|+|x- 3 |. (1) 当 a= 1 时 , 求 f ( x ) 的最小值 ; (2) 若不等式 f ( x ) ≤ 3 的解集非空 , 求 a 的取值范围 . 解 (1) 当 a= 1 时 , f ( x ) =|x- 1 |+|x- 3 | ≥ |x- 1 -x+ 3 |= 2, ∴ f ( x ) 的最小值为 2, 当且仅当 1 ≤ x ≤ 3 时取得最小值 . (2) ∵ x ∈ R 时 , 恒有 |x-a|+|x- 3 | ≥ | ( x-a ) - ( x- 3) |=| 3 -a| , ∴ 不等式 f ( x ) ≤ 3 的解集非空 , | 3 -a| ≤ 3, ∴ 0 ≤ a ≤ 6 .查看更多