2017-2018学年吉林省辽源五中高二下学期第一次月考数学（理）试题 Word版

2017-2018学年吉林省辽源五中高二下学期第一次月考数学（理）试题 Word版

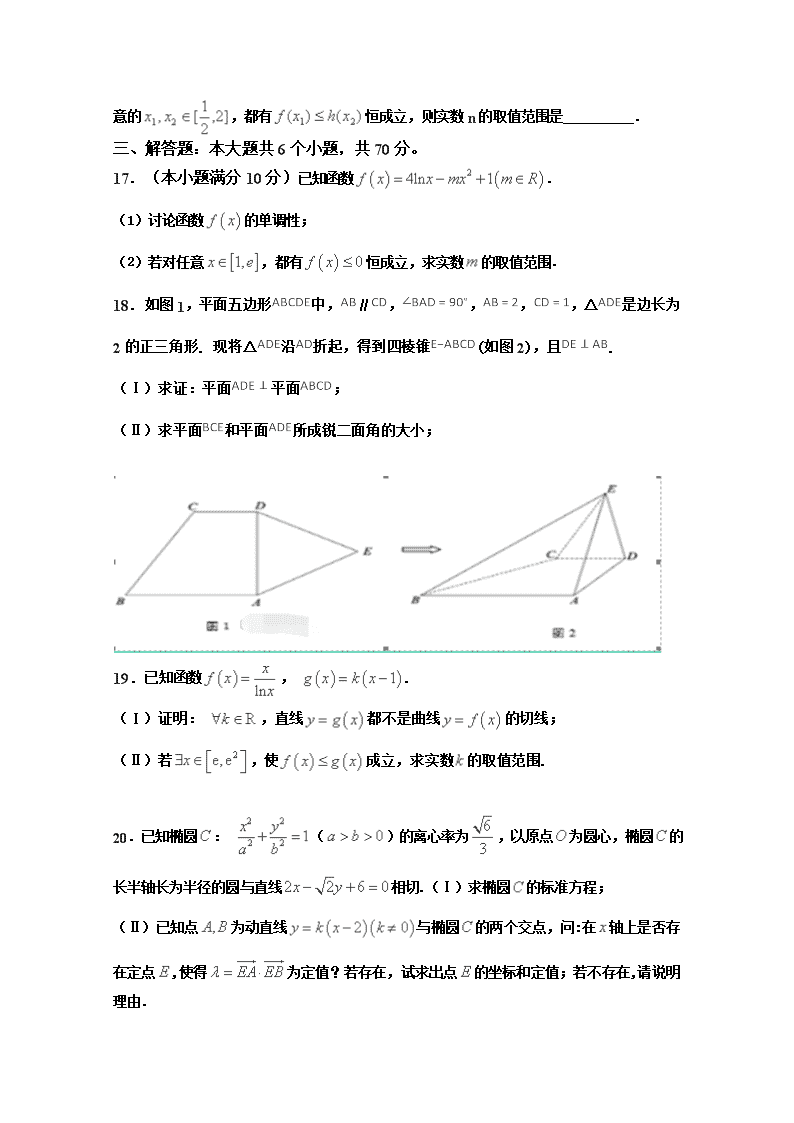
辽源 五中 ‎2017-2018学年度下学期高二数学第一次月考试题（理）‎ ‎ 一、选择题( 本题共12小题，每小题5分，共60分。请将答案写在答题纸的相应表格中)‎ ‎1．已知，则等于（ ）‎ A. B. C. D. ‎ ‎2．（ ）‎ A. 2 B. 6 C. 10 D. 8‎ ‎3．已知函数，则（ ）‎ A. B. ‎ C. D. ‎ ‎4．．若 在 上是减函数，则 的取值范围是（ ）‎ A. B. C. D. ‎ ‎5．函数的导函数为，若恒有成立，且，则不等式的解集为( )‎ A. B. C. D. ‎ ‎6．已知定义域为的奇函数的导函数为，当时， ，若， ， ，则， ， 的大小关系正确的是（ ）‎ A. B. C. D. ‎ ‎7. ．已知a≥0，函数f(x)＝(x2－2ax)ex，若f(x)在[－1,1]上是单调减函数，则a的取值范围是(　　)‎ A. B. C. D. ‎ ‎8. 已知函数y ＝xf′(x)的图象如下图所示，其中f′(x)是函数f(x)的导函数，函数y＝f(x)‎ 的图象大致是图中的(　　)‎ A. B. C. D. ‎ ‎9．若函数在（2,3）上有极大值，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎10．已知任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有对称中心M（x0，f（x0）），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x）=0．若函数f（x）=x3﹣3x2，则f（）+f（）+f（）+…+f（）=（　　）‎ ‎　‎ A．‎ ‎4027‎ B．‎ ‎﹣4027‎ C．‎ ‎8054‎ D．‎ ‎﹣8054‎ ‎11. 若函数在上存在两个极值点，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎ 12. 若函数在时有唯一零点，求实数的取值范围（　　）‎ A． B． C． D. ‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 由曲线与直线所围成的平面图形的面积为 ．‎ ‎14. 已知函数f（x）=lnx+tanα（α∈（0，））的导函数为f′（x），若使得f′（x0）=f（x0）立的x0＜1，则实数α的取值范围为 ．‎ ‎15．已知,当时，不等式恒成立，则的取值范围是 .‎ ‎16. 已知函数，（e 为自然对数的底数），如果对任意的，都有恒成立，则实数n的取值范围是 ．‎ 三、解答题：本大题共6个小题，共70分。 ‎ ‎17．（本小题满分10分）已知函数.‎ ‎（1）讨论函数的单调性；‎ ‎（2）若对任意，都有恒成立，求实数的取值范围.‎ ‎18．如图1，平面五边形中，∥，，，，△是边长为2的正三角形. 现将△沿折起，得到四棱锥(如图2)，且.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求平面和平面所成锐二面角的大小；‎ ‎19．已知函数， .‎ ‎（Ⅰ）证明： ，直线都不是曲线的切线；‎ ‎（Ⅱ）若，使成立，求实数的取值范围.‎ ‎20．已知椭圆： （）的离心率为，以原点为圆心，椭圆的长半轴长为半径的圆与直线相切.（Ⅰ）求椭圆的标准方程；‎ ‎（Ⅱ）已知点为动直线与椭圆的两个交点，问:在轴上是否存在定点,使得为定值？若存在，试求出点的坐标和定值；若不存在,请说明理由.‎ ‎21．设函数．‎ ‎（1）当时，在上恒成立，求实数的取值范围；‎ ‎（2）当时，若函数在上恰有两个不同的零点，求实数的取值范围；‎ ‎（3）是否存在常数，使函数和函数在公共定义域上具有相同的单调性？若存在，求出的取值范围；若不存在，请说明理由．‎ ‎22已知函数， .‎ ‎（Ⅰ）若函数为定义域上的单调函数，求实数的取值范围；‎ ‎（Ⅱ）当时，函数的两个极值点为， ，且.证明： .‎ 理科答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B B A D A C C B D C B ‎13. 【答案】‎ ‎14. 【答案】‎ ‎15：【答案】‎ ‎16【答案】‎ ‎17. （1）当时， 在为增函数；当时, 在为增函数，在为减函数；（2）.‎ ‎18（Ⅰ）略；（Ⅱ）..‎ ‎19. （Ⅰ）的定义域为， ，直线过定点，‎ 若直线与曲线相切于点（且），则 ，即 ‎，①‎ 设， ，则，所以在上单调递增，又，从而当且仅当时，①成立，这与矛盾.‎ 所以， ，直线都不是曲线的切线；‎ ‎（2）‎ ‎20‎ ‎（Ⅰ）;（Ⅱ）.‎ ‎21.‎ ‎（1）；（2）；（3）．‎ ‎1（1）当时，由得，‎ ‎∵，∴，∴有在上恒成立，‎ 令，由得，‎ 当，∴在上为减函数，在上为增函数，‎ ‎∴，∴实数的取值范围为；‎ ‎（2）当时，函数，‎ 在上恰有两个不同的零点，即在上恰有两个不同的零点，‎ 令，则，‎ 当，；当，，‎ ‎∴在上单减，在上单增，，‎ 又，如图所示，所以实数的取值范围为． ‎ ‎（3）函数和函数在公共定义域为，‎ ‎∴在单调递减，在上单调递增，‎ 函数，‎ 时，恒成立，在上单调递增，不合题意，‎ 时，当时，当时，，‎ 在上单调递减，在上为单调递增，‎ 要使与具有相同的单调性，须，解得．‎ 存在常数时，使与具有相同的单调性．‎ ‎22（Ⅰ）函数的定义域为．　‎ 由题意 ， ， .‎ ‎①若，即，则恒成立，则在上为单调减函数；‎ ‎②若，即，方程的两个根为， ，当时， ，所以函数单调递减，当时， ，所以函数单调递增，不符合题意．　‎ 综上，若函数为定义域上的单调函数，则实数的取值范围为.‎ ‎（Ⅱ）因为函数有两个极值点，所以在上有两个不等的实根，‎ 即有两个不等的实根， ，‎ 可得，且，‎ 因为，则，可得.‎ ‎ ，‎ ‎. ‎ 令， ， ，‎ ‎∵，‎ 又， 时， ，‎ 而，故在上恒成立，‎ 所以在上恒成立，‎ 即在上单调递减，‎ 所以，得证．‎