2018-2019学年辽宁省阜新二高高二上学期第一次月考数学（理）试题 Word版

2018-2019学年辽宁省阜新二高高二上学期第一次月考数学（理）试题 Word版

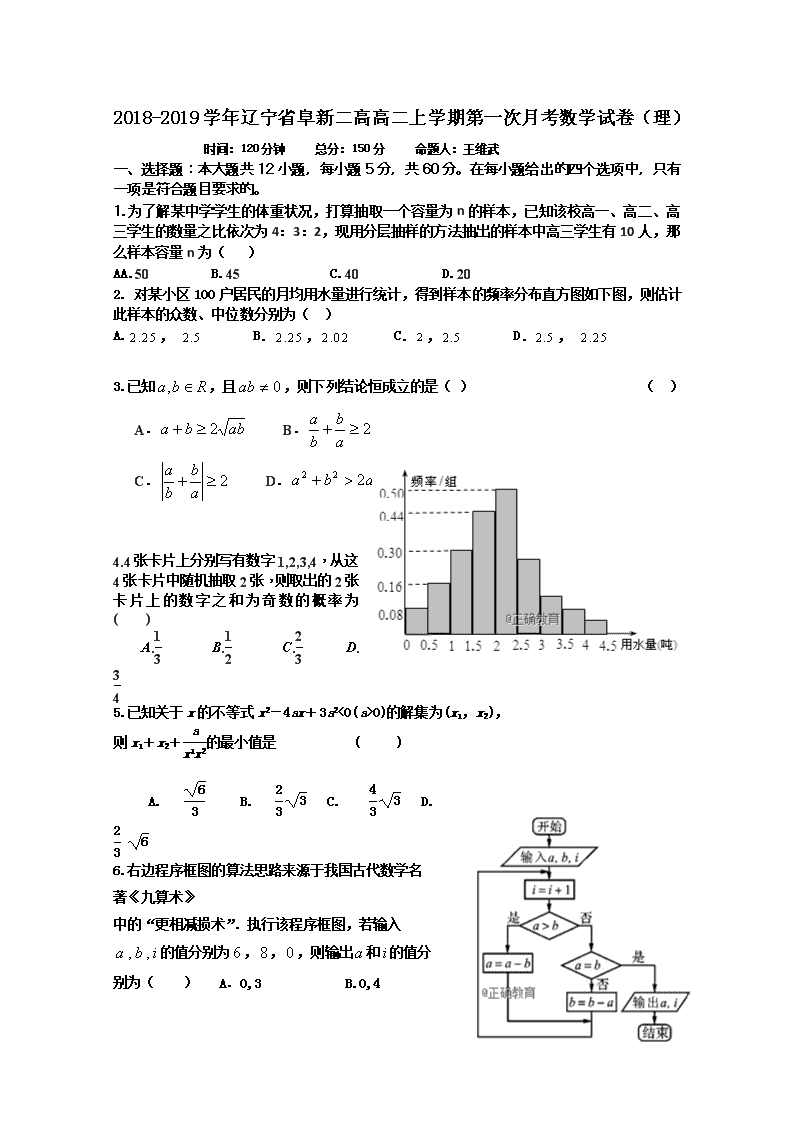
‎2018-2019学年辽宁省阜新二高高二上学期第一次月考数学试卷（理）‎ ‎ 时间：120分钟 总分：150分 命题人：王维武 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.为了解某中学学生的体重状况，打算抽取一个容量为n的样本，已知该校高一、高二、高三学生的数量之比依次为4：3：2，现用分层抽样的方法抽出的样本中高三学生有10人，那么样本容量n为（ ）‎ AA.50 B.45 C.40 D.20‎ ‎2. 对某小区100户居民的月均用水量进行统计，得到样本的频率分布直方图如下图，则估计此样本的众数、中位数分别为（ ）‎ A.， B．， C．， D．， ‎ ‎3.已知，且，则下列结论恒成立的是（ ） （ ）‎ ‎ A． B． ‎ ‎ C． D．‎ ‎ ‎ ‎4.4张卡片上分别写有数字1,2,3,4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为 (　　)‎ A. B. C. D. ‎5.已知关于x的不等式x2－4ax＋3a2<0(a>0)的解集为(x1，x2)，‎ 则x1＋x2＋的最小值是 ( 　　)‎ ‎ A. B. C. D. ‎ ‎6.右边程序框图的算法思路来源于我国古代数学名著《九算术》‎ 中的“更相减损术”．执行该程序框图，若输入的值分别为，，，则输出和的值分别为（ ） A．0,3 B.0,4 C2,3 D 2,4‎ ‎7.在区域，内任取一点（x，y），满足的概率为（ ）A． B． C． D．‎ ‎8.已知五个数据的平均数等于2，方差等于2，现将最后一个数据4去掉，则剩下的四个数据的方差为（ ）A． B． C．1 D． ‎9.已知向量满足，与的夹角为，若对一切实数，恒成立，则的取值范围是（ ）‎ A． B． C． D．‎ ‎10.已知等比数列{an}的各项均为正数，公比q≠1，设P＝()，Q＝，则P与Q的大小关系是(　　)A．P≥Q B．P＜Q C．P≤Q D．P＞Q ‎11.设，，若，且不等式恒成立，则的取值范围是（ ）‎ ‎ A．或 B．或 ‎ C． D．‎ ‎12.已知当时，不等式恒成立，则实数a的取值范围是（ ）‎ A． B． C． D． ‎ 二、填空题：本大题共4个小题，每小题5分，共20分。把答案填在题中横线上。‎ ‎13、数列的前项和，则数列的通项公式为 ‎ ‎14、执行如图的程序框图，若输入的a，b，k分别为1,2,3，则输出的M= ‎ ‎15、已知x>0，y>0，lg2x＋lg8y＝lg2则＋的最小值为 ‎ ‎16、关于的方程的两实根为，若 ‎，则的取值范围是_______‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤。‎ ‎17、（1）已知a>0，b>0，ab -（a＋b）＝1，求a＋b的最小值 ‎ ‎（2）已知x>0，y>0，且2x＋5y＝20.求u＝lg x＋lg y的最大值 ‎18.（1）若不等式ax2+ 4x十a＞1—2x2对任意x∈R均成立，求实数a的取值范围．‎ ‎（2）解关于的不等式 ‎ ‎ 高二数学试卷理第2页(共3页)‎ ‎19、已知求①的最值；‎ ‎ ②的最值；‎ ‎ ③中的范围。‎ ‎ 20. 某老师对本校2016届高三文科学生某次联考的数学成绩进行分析，抽取了20名学生的成绩作为样本进行分析，分数用茎叶图记录如图所示（部分数据丢失），得到频率分布表如下：‎ 分数段(分)‎ 频数 频率 ‎[50,70)‎ a ‎[70,90)‎ ‎0.25‎ ‎[90,110)‎ ‎[110,130)‎ b ‎[130,150)‎ 合计 茎 叶 ‎5‎ ‎6‎ ‎6‎ ‎8‎ ‎7‎ ‎　‎ ‎8‎ ‎0‎ ‎2‎ ‎6‎ ‎9‎ ‎　‎ ‎10‎ ‎0‎ ‎2‎ ‎6‎ ‎6‎ ‎11‎ ‎6‎ ‎8‎ ‎12‎ ‎8‎ ‎13‎ ‎6‎ ‎14‎ ‎2‎ ‎　（1）求表中的值及分数在范围内的学生数，并估计这次考试全体文科学生数学成绩及格率（分数在范围为及格）；‎ ‎（2）从大于等于110分的学生中随机选2名学生得分，求2名学生的平均得分大于等于130分的概率.‎ ‎21、某研究性学习小组对春季昼夜温差大小与某种花卉种子发芽多少间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料：‎ 日期 ‎3月1日 ‎3月2日 ‎3月3日 ‎3月4日 ‎3月5日 温差x/ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数y（颗）‎ ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 该学习小组确定的研究方案是：先从这样5组数据中选取3组求线性回归方程，剩下的2组数据用于回归方程的检验。‎ （1） 请根据3月2日至3月4日的数据，求出y关于x的回归方程；‎ （2） 若由线性回归方程得到的估计数据与所选的验证数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的。试问（1）所得的线性回归方程是否可靠？‎ ‎（，）‎ ‎22、已知各项均不相等的等差数列的前五项和，且成等比数列．‎ ‎（1）求数列的通项公式；‎ ‎（2）设为数列的前项和，若存在，使得成立．求实数的 取值范围．‎ 数学理答案 ‎1-5BBCCC 6-10DCACD 11-12 CD ‎13 ‎ ‎14.4 ‎ ‎15.5‎ ‎16.(-1.25,-0.5)‎ ‎17.(1)∵x>0，y>0，∴由基本不等式，得2x＋5y≥2.‎ ‎∵2x＋5y＝20，∴2≤20，xy≤10，当且仅当2x＝5y时，等号成立．‎ 因此有解得此时xy有最大值10.‎ ‎∴u＝lg x＋lg y＝lg(xy)≤lg 10＝1.∴当x＝5，y＝2时，u＝lg x＋lg y有最大值1.‎ ‎18(1)原不等式可化为 显然时不合题意，所以要使不等式对于任意的恒成立，必须有且 即解得，实数的取值范围为 ‎ (2) 因式分解得，‎ 若不等式化为，则解集为 若时，方程的两根分别为 ‎①若则，所以解集为 ‎②若则，所以解集为或 ‎③若则不等式化为，所以解集为 ‎④若则，所以解集为或 ‎19（1）（1,13）（2）（16/13,32）（3）（0,0.5）‎ ‎20.由茎叶图可知分数在[50,70)范围内的有2人，在[110,130)范围内的有3人，‎ ‎∴，b＝3． …………(2分)‎ 又分数在[110,150)范围内的频率为，‎ ‎∴分数在[90,110)范围内的频率为1－0.1－0.25－0.25＝0.4，‎ ‎∴分数在[90,110)范围内的人数为20×0.4＝8，‎ 由茎叶图可知分数[100,110)范围内的人数为4人，‎ ‎∴分数在[90,100)范围内的学生数为8－4＝4（人）．…………(4分)‎ 从频率分布表可知分数在[90,150)范围内的频率为0.25+0.4=0.65， ‎ 所以估计全校数学成绩及格率为65％ …………(6分)‎ ‎（2）设表示事件“大于等于110分的学生中随机选2名学生得分，平均得分大于等于130分”，由茎叶图可知大于等于110分有5人，记这5人分别为，…………(7分)‎ 则选取学生的所有可能结果为：‎ ‎,，‎ 基本事件数为10，…………(9分)‎ 事件“2名学生的平均得分大于等于130分”也就是“这两个学生的分数之和大于等于260”，所以可能结果为：（118,142），（128,136），（128,142），（136, 142），‎ 共4种情况，基本事件数为4， …………(11分)‎ 所以． …………(12分)‎