2017-2018学年湖南省岳阳市第一中学高二下学期期末考试数学（理）试题-解析版

2017-2018学年湖南省岳阳市第一中学高二下学期期末考试数学（理）试题-解析版

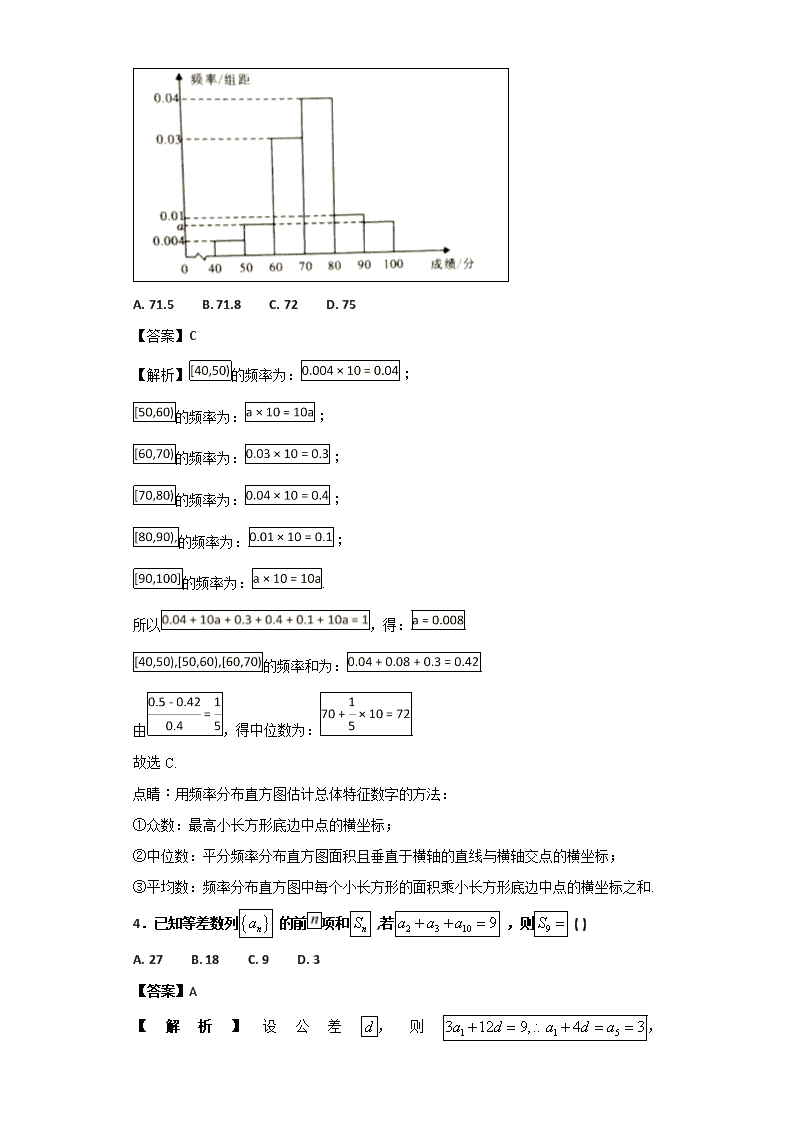
绝密★启用前 湖南省岳阳市第一中学2017-2018学年高二下学期期末考试数学（理）试题 评卷人 得分 一、单选题 ‎1．设复数满足，则（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】,化为， ，故选A.‎ ‎2．若集合，，则下列结论中正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：先求出集合和集合，由此根据集合的关系，得到答案.‎ 详解：由题意，集合，，‎ 所以，故选C.‎ 点睛：本题主要考查了集合的运算，其中正确求解集合是解答的关键，着重考查了推理与预算能力.‎ ‎3．为了解某校一次期中考试数学成绩情况，抽取100位学生的数学成绩，得如图所示的频率分布直方图，其中成绩分组区间是 ，则估计该次数学成绩的中位数是（ ）‎ A. 71.5 B. 71.8 C. 72 D. 75‎ ‎【答案】C ‎【解析】的频率为：；‎ 的频率为：；‎ 的频率为：；‎ 的频率为：；‎ 的频率为：；‎ 的频率为：.‎ 所以，得：.‎ 的频率和为：.‎ 由，得中位数为：.‎ 故选C.‎ 点睛：用频率分布直方图估计总体特征数字的方法：‎ ‎①众数：最高小长方形底边中点的横坐标；‎ ‎②中位数：平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标；‎ ‎③平均数：频率分布直方图中每个小长方形的面积乘小长方形底边中点的横坐标之和.‎ ‎4．已知等差数列 的前项和 ,若 ，则 ( )‎ A. 27 B. 18 C. 9 D. 3‎ ‎【答案】A ‎【解析】设公差，则， ‎ ‎，故选A.‎ ‎5．设曲线在点处的切线与直线平行，则（ ）‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】‎ 试题分析：由的导数为，则在点处的切线斜率为，由切线与直线平行，所以，故选D．‎ 考点：利用导数研究曲线在某点处的切线方程．‎ ‎6．在圆中，弦的长为4，则（ ）‎ A. 8 B. -8 C. 4 D. -4‎ ‎【答案】A ‎【解析】分析：根据平面向量的数量积的定义，老鹰圆的垂径定理，即可求得答案.‎ 详解：如图所示，在圆中，过点作于，则为的中点，‎ 在中，，可得，‎ 所以，故选A.‎ 点睛：本题主要考查了平面向量的数量积的运算，其中解答中涉及到圆的性质，直角三角形中三角函数的定义和向量的数量积的公式等知识点的综合运用，着重考查了分析问题和解答问题的能力.‎ ‎7．如图，点为正方体的中心，点为棱的中点，点为棱的中点，则空间四边形在该正方体的面上的正投影不可能是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：根据空间四边形在正方体前后面、上下面和左右面上的正投影，即可得到正确的选项.‎ 详解：空间四边形在正方体前后面上的正投影是A选项；‎ 空间四边形在正方体前上下上的正投影是B选项；‎ 空间四边形在正方体左右面上的正投影是D选项，故选C.‎ 点睛：本题主要考查了平行投影和平行投影的作法的应用问题，主要同一图形在不同面上的投影不一定相同，属于基础题，着重考查了空间推理能力.‎ ‎8．已知O为坐标原点,抛物线y2=2x与过焦点的直线交于A,B两点,则 的值是 A. B. C. 3 D. 3‎ ‎【答案】B ‎【解析】抛物线的焦点为,当直线l与x轴垂直时， ,‎ 所以 ‎9．已知函数.若关于的方程有两个不同的实根，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】分析：将方程恰有两个不同的实根，转化为方程恰有两个不同的实根，在转化为一个函数的图象与一条折线的位置关系，即可得到答案.‎ 详解：方程恰有两个不同的实根，转化为方程恰有两个不同的实根，‎ 令，，‎ 其中表示过斜率为1或的平行折线，‎ 结合图象，可知其中折线与曲线恰有一个公共点时，，‎ 若关于的方程恰有两个不同的实根，则实数的取值范围是，故选B.‎ 点睛：本题主要考查了方程根的存在性及根的个数的判断问题，其中把方程的实根的个数转化为两个函数的图象的交点的个数，作出函数的图象是解答的关键，着重考查了转化思想方法，以及分析问题和解答问题的能力.‎ ‎10．如图，四个相同的直角三角形与中间的小正方形拼成一个大正方形，已知小正方形的外接圆恰好是大正方形的内切圆，现在大正方形内随机取一点，则此点取自阴影部分的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】分析：设大正方形的边长为1，其内切圆的直径为1，则小正方形的边长为，从而阴影部分的面积为，由此利用几何概型能求出在大正方形内随机取一点，则此点取自阴影部分的概率.‎ 详解：设大正方形的边长为1，其内切圆的直径为1，则小正方形的边长为，‎ 所以大正方形的面积为1，圆的面积为，小正方形的面积为，‎ 则阴影部分的面积为，‎ 所以在大正方形内随机取一点，则此点取自阴影部分的概率.‎ 点睛：本题主要考查了面积比的几何概型及其概率的计算问题，其中根据题意，准确求解阴影部分的面积是解答本题的关键，着重考查了推理与运算能力，以及函数与方程思想的应用，属于基础题.‎ ‎11．已知双曲线的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点. 设A，B到双曲线的同一条渐近线的距离分别为和，且，则双曲线的方程为 A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：由题意首先求得A,B的坐标，然后利用点到直线距离公式求得b的值，之后求解a的值即可确定双曲线方程.‎ 详解：设双曲线的右焦点坐标为（c>0），则，‎ 由可得： ，‎ 不妨设： ，‎ 双曲线的一条渐近线方程为： ，‎ 据此可得： ， ，‎ 则，则，‎ 双曲线的离心率： ，‎ 据此可得： ，则双曲线的方程为.‎ 本题选择C选项.‎ 点睛：求双曲线的标准方程的基本方法是待定系数法．具体过程是先定形，再定量，即先确定双曲线标准方程的形式，然后再根据a，b，c，e及渐近线之间的关系，求出a，b的值．如果已知双曲线的渐近线方程，求双曲线的标准方程，可利用有公共渐近线的双曲线方程为，再由条件求出λ的值即可.‎ ‎12．已知四棱锥的底面是正方形，侧棱长均相等，是线段上的点（不含端点）.设与所成的角为，与平面所成的角为，二面角的平面角为，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】分析：作出三个角，表示出三个角的正弦会正切值，根据三角函数的单调性，即可得出三个角的大小关系.‎ 详解：由题意可知点在底面的射影为正方形的中心，‎ 作作，交于，过底面的中心作交于，‎ 连接，取的中点，连接，则，‎ 则，显然三个角都为锐角， ‎ 其中，其中，所以，‎ 又，其中，所以，‎ 所以，故选D.‎ 点睛：本题主要考查了空间角的计算，以及三角函数的应用，其中根据异面直线所成角、直线与平面所成角和二面角的定义得出，再利用三角函数的定义表示出的正弦值和正切值是解答的关键，着重考查了推理与运算能力和空间想象能力，属于中档试题.‎ 第II卷（非选择题）‎ 请点击修改第II卷的文字说明 评卷人 得分 二、填空题 ‎13．若实数，满足条件，则的最大值为__________．‎ ‎【答案】6‎ ‎【解析】分析：现根据约束条件画出可行域，再利用几何意义求最值，求出最优解，然后求解的最大值即可.‎ 详解：现根据实数满足条件，画出可行域，‎ 如图所示，‎ 由目标函数，则，‎ 结合图象可知，当直线过点时，‎ 目标函数取得最大值，此时最大值为.‎ 点睛：本题主要考查了简单的线性规划求最大值，其中画出约束条件所表示的平面区域，根据直线的几何意义求解是解答的关键，着重考查了推理与运算能力.‎ ‎14．已知数列的前项和，则__________．‎ ‎【答案】64‎ ‎【解析】分析：由题意，根据数列的和的关系，求得，即可求解的值.‎ 详解：由题意，数列的前项和为，‎ 当时，，所以 点睛：本题主要考查了数列中和的关系，其中利用数列的和的关系求解数列的通项公式是解答的关键，着重考查了推理与运算能力.‎ ‎15．展开式中的常数项为__________．‎ ‎【答案】24‎ ‎【解析】分析：由题意，求得二项式的展开式的通项为，即可求解答案.‎ 详解：由题意，二项式的展开式的通项为，‎ 令，则.‎ 点睛：本题主要考查了二项式定理的应用，其中熟记二项展开式的通项公式是解答的关键，着重考查了推理与运算能力.‎