命题角度4-3 空间位置关系证明与二面角求解（第01期）-2018年高考数学（理）备考之百强校大题狂练系列

命题角度4-3 空间位置关系证明与二面角求解（第01期）-2018年高考数学（理）备考之百强校大题狂练系列

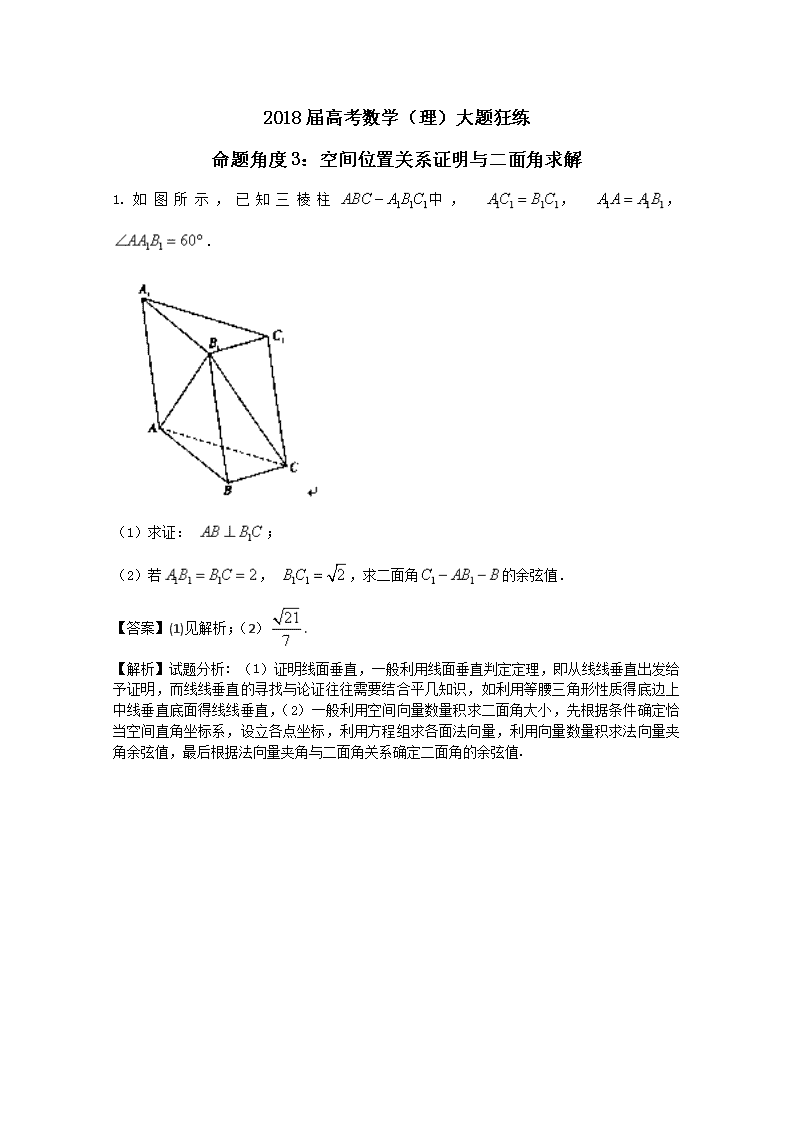
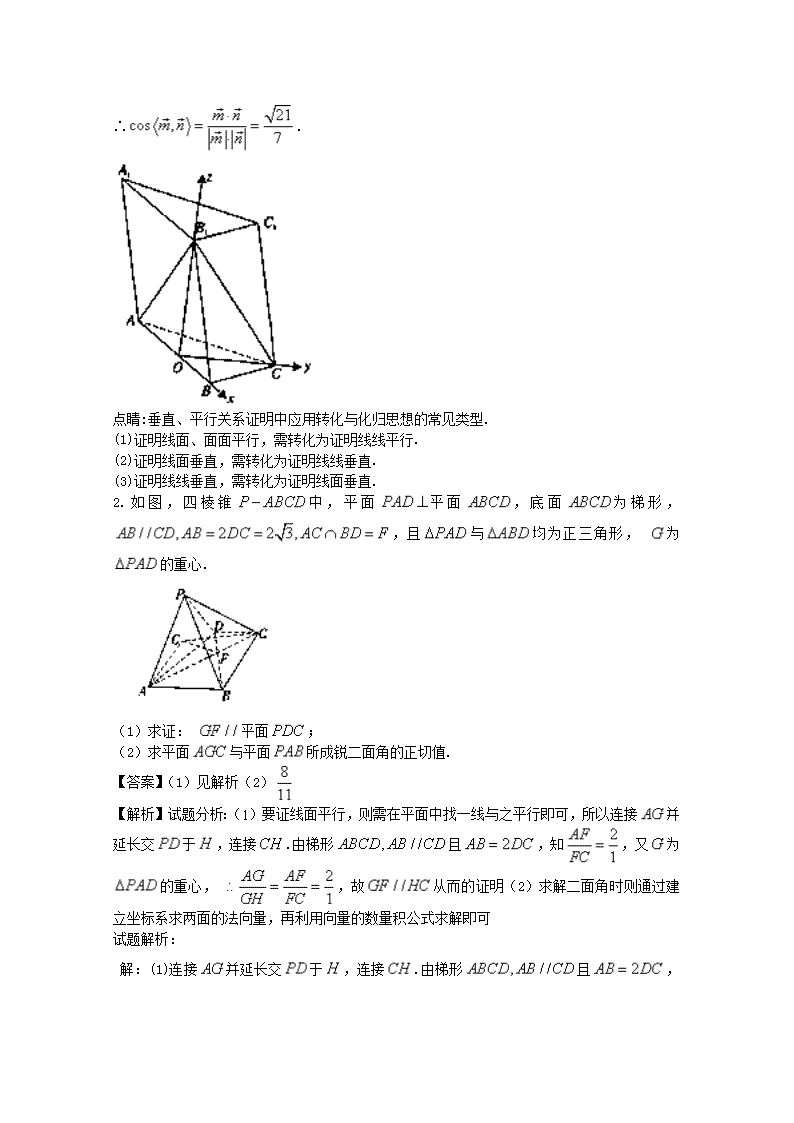
‎2018届高考数学（理）大题狂练 命题角度3：空间位置关系证明与二面角求解 ‎1.如图所示，已知三棱柱中， ， ， ．‎ ‎（1）求证： ；‎ ‎（2）若， ，求二面角的余弦值．‎ ‎【答案】(1)见解析；（2）.‎ ‎【解析】试题分析: （1）证明线面垂直，一般利用线面垂直判定定理，即从线线垂直出发给予证明，而线线垂直的寻找与论证往往需要结合平几知识，如利用等腰三角形性质得底边上中线垂直底面得线线垂直，（2）一般利用空间向量数量积求二面角大小，先根据条件确定恰当空间直角坐标系，设立各点坐标，利用方程组求各面法向量，利用向量数量积求法向量夹角余弦值，最后根据法向量夹角与二面角关系确定二面角的余弦值.‎ ‎（2）∵为等边三角形， ，∴，‎ ‎∵在中， ， ， 为中点，‎ ‎∴，‎ ‎∵， ，∴，‎ ‎∴，‎ 又，‎ ‎∴平面．‎ 以为原点， ， ， 方向为， ， 轴的正向，建立如图所示的坐标系， ， ， ， ，‎ 则，则， ， ，‎ 则平面的一个法向量，‎ 设为平面的法向量，则令，∴，‎ ‎∴，‎ ‎∴．‎ 点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.‎ ‎(1)证明线面、面面平行，需转化为证明线线平行.‎ ‎(2)证明线面垂直，需转化为证明线线垂直.‎ ‎(3)证明线线垂直，需转化为证明线面垂直.‎ ‎2.如图，四棱锥中，平面平面，底面为梯形， ，且与均为正三角形， 为的重心.‎ ‎（1）求证： 平面；‎ ‎（2）求平面与平面所成锐二面角的正切值.‎ ‎【答案】（1）见解析（2） ‎【解析】试题分析：（1）要证线面平行，则需在平面中找一线与之平行即可，所以连接并延长交于，连接.由梯形且，知，又为的重心， ，故从而的证明（2）求解二面角时则通过建立坐标系求两面的法向量，再利用向量的数量积公式求解即可 试题解析：‎ ‎ 解：(1)连接并延长交于，连接.由梯形且 ‎，知，又为的重心， ，故.又平面平面平面.‎ ‎(2) 平面平面与均为正三角形，延长交的中点，连接平面，以为原点建立如图所示的空间直角坐标系， ，‎ ，设，可得，设平面的一个法向量为，由，令，得，同理可得平面的一个法向量，所以平面与平面所成锐二面角的正切值为.‎ 点睛：证线面平行首先要明确和熟悉其判定定理，在面内找一线与一直线平行即可，求面面角时则通常经过建立直角坐标系，求出两面的法向量，再通过向量夹角公式计算即可 ‎3.如图，在三棱柱中，平面平面， ， ， ， ， 为的中点．‎ ‎（1）求证： 平面；‎ ‎（2）求二面角的余弦值．‎ ‎【答案】（1）见解析;（2）．‎ ‎【解析】试题分析：证明线面垂直，只需寻求线线垂直，利用题目提供的面面垂直，可以得到线面垂直，进而说明线线垂直；求二面角可采用建立空间直角坐标系，借助法向量求解，本题需要设，根据条件求出，再利用法向量求出二面角的余弦.‎ 试题解析：（1）证明：∵， 为的中点，∴，又平面平面，平面平面， 平面，∴平面，又平面，∴．又， ，∴面．‎ 则由余弦定理得．‎ ，设与交于点，则 ， ，而 ，则．‎ 于是，即，∴或（舍）‎ 容易求得： ，而．‎ 故，由面面，则面，过作于，连，则为二面角的平面角，由平面几何知识易得， ．‎ ‎∴．‎ 方法二：以点为原点， 为轴，过点与平面垂直的直线为轴，建立如图所示的空间直角坐标系，设， ，则， ， ， ．‎ ‎∴， ．由，得，∴，则， ，于是， ，‎ ‎∵，‎ 不妨设平面的法向量，则，‎ 故二面角的余弦值为．‎ ‎【点睛】证明线面垂直，只需寻求线线垂直，利用题目提供的面面垂直，可以得到线面垂直，进而说明线线垂直；求二面角的方法有两种，传统方法为“作、证、求”，用空间向量，借助法向量更容易一些.‎ ‎4.如图，在梯形中， ， ，四边形为矩形，且平面， .‎ ‎（1）求证： 平面；‎ ‎（2）点在线段（含端点）上运动，当点在什么位置时，平面与平面所成锐二面角最大，并求此时二面角的余弦值.‎ ‎【答案】（1）见解析（2） ‎【解析】试题分析：‎ ‎（1）由， 可得.由可得.从而平面 ‎（2）分别以直线， ， 为轴， 轴， 轴的如图所示建立空间直角坐标系，令 (). 平面的一个法向量=(1, , ), =(1,0,0)是平面的一个法向量. ∵,∴当时， 有最小值.‎ 试题解析： (I)在梯形中，∵，设，‎ 又∵,∴，∴ ‎∴∴. ‎ ‎∵， ，‎ ‎∴，而，‎ ‎∴ ‎ ‎∵ ∴. ‎ ‎(II)由(I)可建立分别以直线， ， 为轴， 轴， 轴的如图所示建立空间直角坐标系，‎ 设，令 (),则 (0，0，0)， (，0，0)， (0，1，0)， (，0，1)，‎ ‎∴=(-，1，0)， =( ，-1，1)， ‎ 设为平面的一个法向量，‎ 由得 取,则=(1, , ), ‎ ‎∵=(1,0,0)是平面的一个法向量,‎ ‎∴ ‎ ‎∵,∴当时， 有最小值，‎ ‎∴点与点重合时，平面与平面所成二面角最大，此时二面角的余弦值为.‎ ‎5.如图，在四棱锥中，底面为正方形， 平面，已知为线段的中点.‎ ‎（I）求证： 平面；‎ ‎（II）求平面与平面所成锐二面角的余弦角.‎ ‎【答案】（1）见解析；（2）.‎ ‎ (II)因为平面平面，‎ 所以.‎ 因为为正方形，所以.‎ 因为平面，‎ 所以平面.‎ 因为平面，所以.‎ 所以以为原点，以所在直线为轴建立如图所示的空间直角坐标系，‎ 则.‎ 因为平面平面,‎ 所以.‎ 因为，所以.‎ 因为四边形为正方形，‎ 所以，‎ 所以.‎ 由四边形为正方形，‎ 得,‎ 所以.‎ 设平面的一个法向量为，又知，‎ 由 令，得，‎ 所以.‎ 设平面的一个法向量为，又知,‎ 由 令，得，‎ 所以.‎ 设平面与平面所成的锐二面角为，‎ 又，‎ 则.‎ 所以平面与平面所成的锐二面角的余弦值为.‎ ‎【方法点晴】本题主要考查线面平行的判定定理以及利用空间向量求二面角的大小，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.‎ ‎6.如图，在三棱台中，平面，，，分别为，的中点．‎ ‎（1）求证：平面；‎ ‎（2）若且，求二面角的大小．‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）利用中位线，有，所以平面平面，所以平面；（2）易得，，两两垂直，以此建立空间直角坐标系，分别计算平面的法向量，利用法向量夹角来计算二面角的余弦值为，所以二面角为.‎ 试题解析：‎ ‎（2）解：由平面，可得平面，‎ 而，，则，‎ 所以，，两两垂直，‎ 故以点为坐标原点，，，所在的直线分别为，，轴建立如图所示的空间直角坐标系．‎ 设，则，，，，，，，‎ 则平面的一个法向量为，‎ 设平面的法向量为，则即 取，则，，，‎ ，易得二面角为锐角，‎ 所以二面角的大小为．‎ 考点：空间向量与立体几何.‎ ‎7. 如图，三棱柱ABC-DEF中，侧面ABED是边长为2的菱形，且‎∠ABE=‎π‎3‎，BC=‎‎21‎‎2‎，四棱锥F-ABED的体积为2，点F在平面ABED内的正投影为G，且G在AE上点M是线段CF上，且CM=‎1‎‎4‎CF．‎ ‎（1）证明：直线GM//‎平面DEF；‎ ‎（2）求二面角M-AB-F的余弦值．‎ ‎【答案】(1)详见解析；（2）‎‎7‎‎85‎‎85‎ ‎【解析】试题分析：（1）通过构造辅助线FH，证明GHFM为平行四边形，即借助线线平行证明线面平行；（2）借助底面四边形的对角线互相垂直，建立空间直角坐标，利用向量方法求解二面角.‎ ‎（Ⅰ）解析：‎ 因为四棱锥F-ABED的体积为2，‎ 即VF-ABED‎=‎1‎‎3‎×‎3‎‎4‎×4×2×FG=2‎，所以FG=‎‎3‎ 又BC=EF=‎‎21‎‎2‎，所以EG=‎‎3‎‎2‎即点G是靠近点A的四等分点，‎ 过点G作GK//AD交DE于点K，所以GK=‎3‎‎4‎AD=‎3‎‎4‎CF，‎ 又MF=‎3‎‎4‎CF，所以MF=GK且MF//GK， ‎ 所以四边形MFKG为平行四边形，‎ 所以GM//FK，所以直线GM//‎平面DEF.‎ ‎（Ⅱ）‎ ‎ ‎ 设AE,BD的交点为O，OB所在直线为x轴，OE所在直线为y轴，过点O作平面ABED 的垂线为z轴，建立空间直角坐标系，如图所示：‎ A(0,-1,0),B(‎3‎,0,0),F(0,-‎1‎‎2‎,‎3‎),M(‎3‎‎3‎‎4‎,-‎5‎‎4‎,‎3‎)‎ BA‎=(-‎3‎,-1,0),BM=(-‎3‎‎4‎,-‎5‎‎4‎,‎3‎),BF=(-‎3‎,-‎1‎‎2‎,‎3‎)‎ 设平面ABM,ABF的法向量为m‎,‎n，‎ ‎{‎m‎·BA=0‎m‎·BM=0‎‎，则m‎=(1,-‎3‎,-1)‎， ‎{‎n‎·BA=0‎n‎·BF=0‎，则n‎=(1,-‎3‎,‎1‎‎2‎)‎ cosθ=m‎·‎n‎|m||n|‎=‎‎7‎‎85‎‎85‎‎，即为所求.‎ 点睛：本题主要考查直线与平面平行的判定定理、二面角、空间向量的应用，以三棱柱为载体，考查借助空间想象能力、逻辑推证、转化能力、运算能力．线面平行的判定方法一是线面平行的判定定理，二是证面面平行，其解题的关键是在面内找到一线与面外一线平行，或由线面平行导出面面平行，性质的运用一般要利用辅助平面；求二面角通常通过建立空间直角坐标系利用空间夹角公式求解．‎ ‎8.如图，在正方形中，点，分别是，的中点，将分别沿，折起，使两点重合于.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎【答案】（Ⅰ）详见解析（Ⅱ） ‎【解析】‎ 试题分析：（Ⅰ）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而线面垂直的证明往往利用线面垂直判定与性质定理，即从线线垂直出发给予证明，而线线垂直的寻找与论证往往需结合平几知识进行：连接交于，则根据等腰三角形性质得，（Ⅱ）求二面角，一般利用空间向量进行求解，先根据条件建立空间直角坐标系，设立各点坐标，利用方程组解出各面法向量，利用向量数量积求法向量夹角，最后根据二面角与向量夹角之间关系求解 试题解析：（Ⅰ）证明：连接交于，连接.‎ 在正方形中，点是中点，点是中点，‎ 所以，‎ 所以，‎ 所以在等腰中，是的中点，且，‎ 因此在等腰中，，‎ 从而，‎ 又，‎ 所以平面，‎ 即平面.…………………6分 所以，‎ 于是，在翻折后的几何体中，为二面角的平面角，‎ 在正方形中，解得，，‎ 所以，在中，，，，‎ 由余弦定理得，‎ 所以，二面角的余弦值为.………………………………12分 设为平面的一个法向量，‎ 由得，‎ 令，得，‎ 又由题知是平面的一个法向量，‎ 所以.‎ 所以，二面角的余弦值为.………………………………12分 考点：空间面面垂直的判定与性质、空间面面夹角 ‎【思路点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.‎ ‎9.如图，四棱锥中， 平面， ， ‎ ， ， 是棱的中点.‎ ‎（Ⅰ）若，求证： 平面；‎ ‎（Ⅱ）求的值，使二面角的平面角最小.‎ ‎【答案】（Ⅰ）见解析; （Ⅱ）.‎ ‎【解析】试题分析：‎ ‎(Ⅰ)利用题意证得， .∴平面.‎ ‎(Ⅱ)建立空间直角坐标系，由题意可得，要使最小，则最大，得.‎ 试题解析：‎ 当时，‎ ‎∵， .‎ ‎∴.‎ 又平面，∴.‎ ‎∴平面.‎ 又平面，‎ ‎∴.‎ 又， 是棱的中点，‎ ‎∴.‎ ‎∴平面.‎ 又易知平面的法向量为.‎ 设二面角的平面角为，‎ 则 要使最小，则最大，即，‎ ‎∴，得 ‎10.如图，在四棱锥中，四边形为梯形， ，且， ‎ 是边长为2的正三角形，顶点在上的射影为点，且， ， .‎ ‎（1）证明：平面平面；‎ ‎（2）求二面角的余弦值.‎ ‎【答案】（1）见解析（2） ‎【解析】试题分析：（1）　取的中点为，连接利用直角三角形的性质，可分别求出的值，由勾股定理得．可得面，可证平面平面；（2）以所在直线为轴， 所在直线为轴，过点作平面的垂线为轴，建立空间直角坐标系，写出各点坐标，求出两个半平面的法向量，利用法向量的夹角与二面角的夹角的关系，可求二面角的余弦值．‎ ‎（Ⅱ）由（Ⅰ）知， ， ，且 所以 面，且面．以所在直线为轴， 所在直线为轴，过点作平面的垂线为轴，建立空间直角坐标系，如图所示： ‎ ， ， ，‎ ‎ 设平面， 的法向量分别为，则 ，则，‎ ，则 ， ‎ ，‎ 所以二面角的余弦值为．‎ 点睛：若分别为二面角的两个半平面的法向量，则二面角的大小满足，二面角的平面角的大小是的夹角(或其补角，需根据观察得出结论)．在利用向量求空间角时，建立合理的空间直角坐标系，正确写出各点坐标，求出平面的法向量是解题的关键．‎ ‎ ‎