高中数学必修2模块检测
模块检测
一、选择题
1.过点A(3,-4),B(-2,m)的直线l的斜率为-2,则m的值为( )
A.6 B.1 C.2 D.4
答案 A
解析 由题意知kAB==-2,∴m=6.
2.在x轴、y轴上的截距分别是-2、3的直线方程是( )
A.2x-3y-6=0 B.3x-2y-6=0
C.3x-2y+6=0 D.2x-3y+6=0
答案 C
解析 由直线的截距式得,所求直线的方程为+=1,即3x-2y+6=0.
3.在空间直角坐标系中,点B是A(1,2,3)在yOz坐标平面内的射影,O为坐标原点,则|OB|等于( )
A. B.
C.2 D.
答案 B
解析 点A(1,2,3)在yOz坐标平面内的射影为B(0,2,3),
∴|OB|==.
4.已知两直线y=ax-2和y=(a+2)x+1互相垂直,则a等于( )
A.2 B.1 C.0 D.-1
答案 D
解析 由题意知(a+2)a=-1⇒a2+2a+1=(a+1)2=0,∴a=-1.也可以代入检验.
5.动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
A.x2+y2=32 B.x2+y2=16
C.(x-1)2+y2=16 D.x2+(y-1)2=16
答案 B
解析 设P(x,y),则由题意可得:2=,化简整理得x2+y2=16,故选B.
6.设长方体的长,宽,高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )
A.3πa2 B.6πa2 C.12πa2 D.24πa2
答案 B
解析 由题意可知,球的直径等于长方体的体对角线的长度,故2R=,解得R=a,所以球的表面积S=4πR2=6πa2.
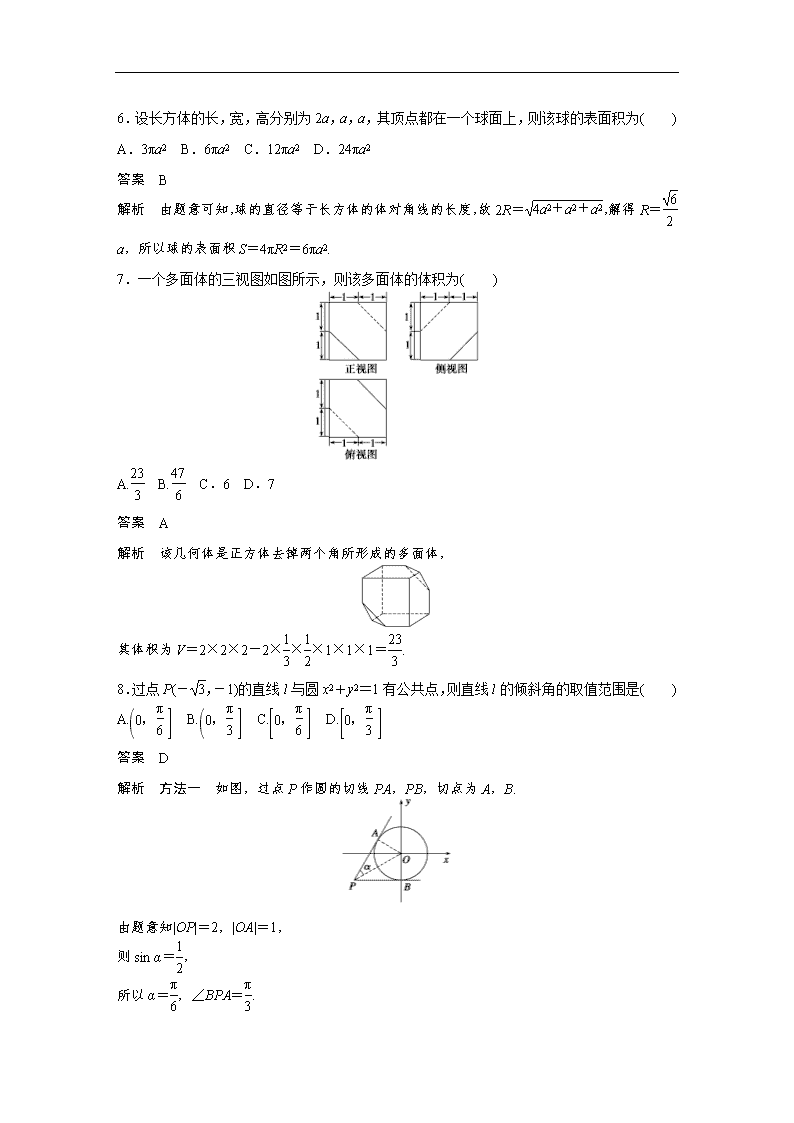
7.一个多面体的三视图如图所示,则该多面体的体积为( )
A. B. C.6 D.7
答案 A
解析 该几何体是正方体去掉两个角所形成的多面体,
其体积为V=2×2×2-2×××1×1×1=.
8.过点P(-,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是( )
A. B. C. D.
答案 D
解析 方法一 如图,过点P作圆的切线PA,PB,切点为A,B.
由题意知|OP|=2,|OA|=1,
则sin α=,
所以α=,∠BPA=.
故直线l的倾斜角的取值范围是.选D.
方法二 设过点P的直线方程为y=k(x+)-1,则由直线和圆有公共点知≤1.
解得0≤k≤.故直线l的倾斜角的取值范围是[0,].
9. 如图所示,在正方体ABCDA1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60°
C.90° D.120°
答案 B
解析 如图,取A1B1的中点M,连接GM,HM.由题意易知EF∥GM,且△GMH为正三角形.
∴异面直线EF与GH所成的角即为GM与GH的夹角∠HGM.而在正三角形GMH中∠HGM=60°,故选B.
10.若曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有四个不同的交点,则实数m的取值范围是( )
A.
B.∪
C.
D.∪
答案 B
解析 C1:(x-1)2+y2=1,
C2:y=0或y=mx+m=m(x+1).
当m=0时,C2:y=0,此时C1与C2显然只有两个交点;
当m≠0时,要满足题意,需圆(x-1)2+y2=1与直线y=m(x+1)有两交点,当圆与直线相切时,m=±,
即直线处于两切线之间时满足题意,则-
0)的公共弦的长为2,则a=________.
答案 1
解析 两圆的方程相减,得公共弦所在的直线方程为(x2+y2+2ay-6)-(x2+y2)=0-4⇒y=,又a>0,结合图象,再利用半径、弦长的一半及弦心距所构成的直角三角形,可知==1⇒a=1.
三、解答题
15.已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m、n的值,使
(1)l1与l2相交于点(m,-1);
(2)l1∥l2;
(3)l1⊥l2,且l1在y轴上的截距为-1.
解 (1)因为l1与l2相交于点(m,-1),
所以点(m,-1)在l1、l2上,
将点(m,-1)代入l2,得2m-m-1=0,解得m=1.
又因为m=1,把(1,-1)代入l1,所以n=7.
故m=1,n=7.
(2)要使l1∥l2,则有
解得或
(3)要使l1⊥l2,则有m·2+8·m=0,得m=0.
则l1为y=-,由于l1在y轴上的截距为-1,
所以-=-1,即n=8.故m=0,n=8.
16. 如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
证明 (1)因为AS=AB,AF⊥SB,
垂足为F,所以F是SB的中点.
又因为E是SA的中点,
所以EF∥AB.
因为EF⊄平面ABC,AB⊂平面ABC,
所以EF∥平面ABC.
同理EG∥平面ABC.又EF∩EG=E,
所以平面EFG∥平面ABC.
(2)因为平面SAB⊥平面SBC,且交线为SB,又AF⊂平面SAB,AF⊥SB,所以AF⊥平面SBC.
因为BC⊂平面SBC,所以AF⊥BC.
又因为AB⊥BC,AF∩AB=A,AF⊂平面SAB,AB⊂平面SAB,所以BC⊥平面SAB.
因为SA⊂平面SAB,所以BC⊥SA.
17. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
(1)证明 在三棱柱ABC-A1B1C1中,
BB1⊥底面ABC,所以BB1⊥AB.
又因为AB⊥BC,
所以AB⊥平面B1BCC1,
又AB⊂平面ABE,所以平面ABE⊥平面B1BCC1.
(2)证明 取AB的中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,
所以FG∥AC,且FG=AC.
因为AC∥A1C1,且AC=A1C1,
所以FG∥EC1,且FG=EC1,
所以四边形FGEC1为平行四边形.所以C1F∥EG.
又因为EG⊂平面ABE,C1F⊄平面ABE,
所以C1F∥平面ABE.
(3)解 因为AA1=AC=2,BC=1,AB⊥BC,
所以AB==.
所以三棱锥E-ABC的体积V=S△ABC·AA1
=×××1×2=.
18.如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=.
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
解 方法一 (1)如图,以O为坐标原点,
OC所在直线为x轴,建立平面直角坐标系xOy.
由条件知A(0,60),C(170,0),
直线BC的斜率kBC=-tan∠BCO=-.
又因为AB⊥BC,
所以直线AB的斜率kAB=.
设点B的坐标为(a,b),
则kBC==-,①
kAB==.②
联立①②解得a=80,b=120.
所以BC==150.
因此新桥BC的长是150 m.
(2)设保护区的边界圆M的半径为r m,OM=d m(0≤d≤60).
由条件知,直线BC的方程为y=-(x-170),
即4x+3y-680=0.
由于圆M与直线BC相切,
故点M(0,d)到直线BC的距离是r,
即r==.
因为O和A到圆M上任意一点的距离均不少于80 m,
所以即
解得10≤d≤35.
故当d=10时,r=最大,即圆面积最大.
所以当OM=10 m时,圆形保护区的面积最大.
方法二 (1)如图,延长OA,CB交于点F.
因为tan∠FCO=,所以sin∠FCO=,cos∠FCO=.
因为OA=60,OC=170,
所以OF=OCtan∠FCO=,
CF==,
从而AF=OF-OA=.
因为OA⊥OC,
所以cos∠AFB=sin∠FCO=.
又因为AB⊥BC,所以BF=AFcos∠AFB=,
从而BC=CF-BF=150.
因此新桥BC的长是150 m.
(2)设保护区的边界圆M与BC的切点为D,
连接MD,则MD⊥BC,
且MD是圆M的半径,并设MD=r m,
OM=d m(0≤d≤60).
因为OA⊥OC,所以sin∠CFO=cos∠FCO.
故由(1)知sin∠CFO====,
所以r=.
因为O和A到圆M上任意一点的距离均不少于80 m,
所以即
解得10≤d≤35.
故当d=10时,r=最大,即圆面积最大.
所以当OM=10 m时,圆形保护区的面积最大.