- 2021-06-21 发布 |
- 37.5 KB |
- 2页
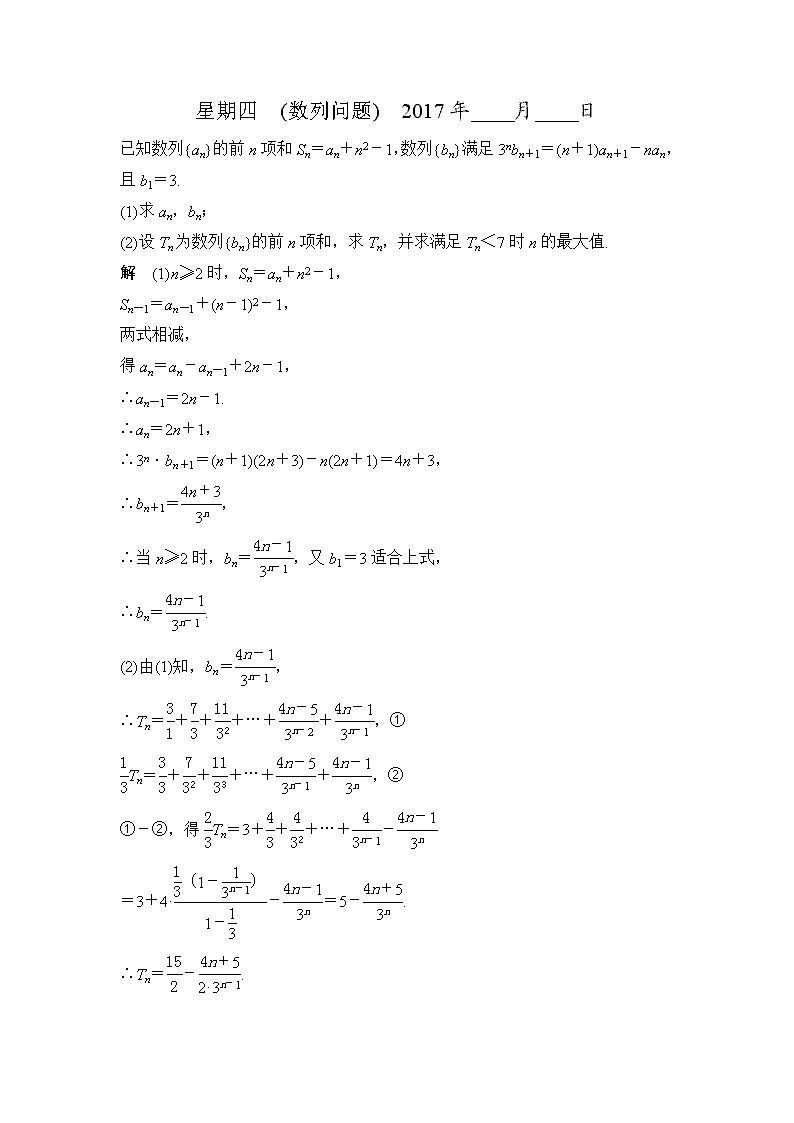

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017届高考数学(文)二轮复习(江苏专用)解答题 第一周 星期四
星期四 (数列问题) 2017年____月____日 已知数列{an}的前n项和Sn=an+n2-1,数列{bn}满足3nbn+1=(n+1)an+1-nan,且b1=3. (1)求an,bn; (2)设Tn为数列{bn}的前n项和,求Tn,并求满足Tn<7时n的最大值. 解 (1)n≥2时,Sn=an+n2-1, Sn-1=an-1+(n-1)2-1, 两式相减, 得an=an-an-1+2n-1, ∴an-1=2n-1. ∴an=2n+1, ∴3n·bn+1=(n+1)(2n+3)-n(2n+1)=4n+3, ∴bn+1=, ∴当n≥2时,bn=,又b1=3适合上式, ∴bn=. (2)由(1)知,bn=, ∴Tn=+++…++,① Tn=+++…++,② ①-②,得Tn=3+++…+- =3+4·-=5-. ∴Tn=-. Tn-Tn+1=-=<0. ∴Tn<Tn+1,即{Tn}为递增数列. 又T3=<7,T4=>7, ∴Tn<7时,n的最大值为3.查看更多