数学理卷·2017届四川省绵阳第一中学高三12月月考（2016

数学理卷·2017届四川省绵阳第一中学高三12月月考（2016

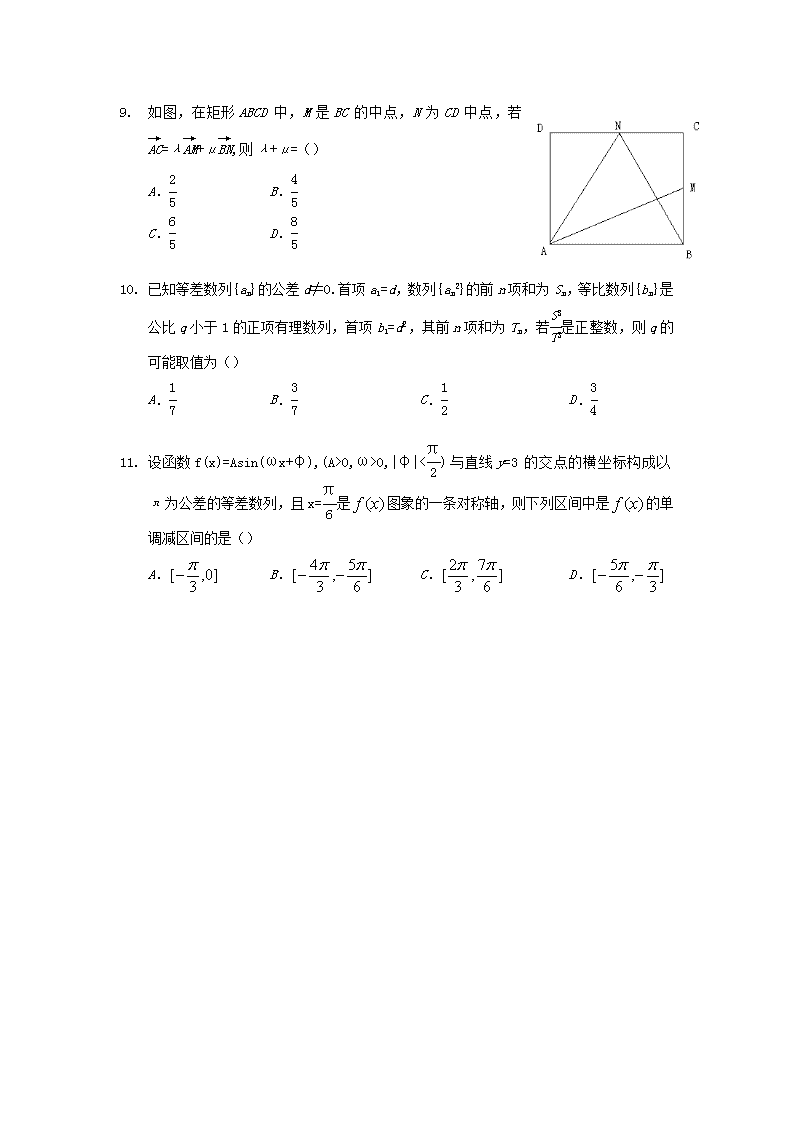
高 2014 级第 5 学期第二次月考试卷 数学（理） 一．选择题 1. 已知复数 为虚数单位）ii iz (21 5  ，则 z 的共轭复数对应的点位于复平面的（） A．第一象限 B．第二象限 C．第三象限 D.第四象限 2. 已知集合 M＝{－1，0，1}，N＝{y｜y＝1+sinπx 2 ,x∈M}，则集合 M∩N 的真子集个数是 （） A．4 B．3 C．2 D．1 3. 设 则且 baRcba  ,,, （） A. bcac  B. ba 11  C. 22 ba  D. 33 ba  4. 已知数列 na 为等差数列，其前 n 项和为 nS ，若 40342017 S ，则 201510093 aaa  = A．2 B．4 C．6 D．8 5. 已知方程 x2 m+1 －y2 m =1 表示双曲线，则实数 m 的取值范围是() A．(-∞,-1) B．(-1,+∞) C．(-∞,-1)∪(0,+∞) D ． (-∞,-1) ∪ (-1,0) 6. 设点 M 是圆 C:x2+y2-4y+3=0 上的一个动点，则点 M 到直线 l:x- 3y+3 3=0 的最大距离 为() A． 12 3  B． 2 31 C． 2 3 D． 22 3  7. 已知点 yx, 满足约束条件 x+y-2≥0 x-2y+4≥0 x-2≤0 ，则 z=3x+y 的最大值与最小值之差为（） A．5 B．6 C．7 D．8 8. 9. 如图，在矩形 ABCD 中，M 是 BC 的中点，N 为 CD 中点，若 →AC=λ→AM+μ→BN,则λ+μ=（） A．2 5 B．4 5 C．6 5 D．8 5 10. 已知等差数列{an}的公差 d≠0.首项 a1 =d，数列{an 2}的前 n 项和为 Sn，等比数列{bn}是 公比 q 小于 1 的正项有理数列，首项 b1=d2，其前 n 项和为 Tn，若S3 T3 是正整数，则 q 的可 能取值为（） A．1 7 B．3 7 C．1 2 D．3 4 11. 设函数 f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<π 2 )与直线 y=3 的交点的横坐标构成以π 为公差的等差数列，且 x=π 6 是 )(xf 图象的一条对称轴，则下列区间中是 )(xf 的单调 减区间的是（） A． ]0,3[  B． ]6 5,3 4[   C． ]6 7,3 2[  D． ]3,6 5[   12. 已知双曲线 C：x2 a2-y2 b2 =1(a>0,b>0)的离心率为 2，双曲线 C 的两条渐近线与抛物线 y2=2px(p>0)交于 A，B 两点，若△OAB(O 为坐标原点)的面积为 4，则抛物线的方程为（） A． xy 82  B． xy 42  C． xy 22  D． xy 342  13. 已 知 函 数 )(xfy  是 定 义 域 为 R 的 偶 函 数 ， 当 0x 时 ， f(x)= 5 4 sin(π 2 x)，（0≤x≤1） (1 4 )x+1，（x>1） ， 若 关 于 x 的 方 程 ).(06)()65()]([5 2 Raaxfaxf  有且仅有 6 个不同的实数根，则实数 a 的取 值范围是 A．(0,1)∪{5 4 } B．∪{5 4 } C．(0,1]∪{5 4 } D．(1,5 4 )∪{0} 二、填空题 14. 若向量→a ,→b 满足|→a |= 3,|→b |=2,→a ⊥(→a -→b )，则→a 与→b 的夹角为______ 15. 已知函数      0,3 0,log)( 4 x xxxf x ，则 ))4 1(( ff _______ 16. 已知在三角形 ABC 中，角 A 和角 B 都是锐角，且 BC tan4tan  ,则 tanA 的最大值为 ______ 17. 已知直线 1 kxy 与抛物线 xy 22  相切于点 M,过点 M 作两条直线，分别与抛物线交 于 A,B 两点，若两直线的斜率之和为 0，则直线 AB 的斜率为_______ 三、解答题 18. (本题满分 12 分) 在等比数列 na 中， 0na , 431 aa ,且 13 a 是 2a 和 4a 的等差中项， 12log  nn ab (1)求数列 nb 的通项公式 (2)若数列 nc 满足 1212 1 1    nn nn bbac ，求数列 nc 的前 n 项和 nT 19. (本题满分 12 分) 已知函数 f(x)= 3sin(3π+x)·cos(π-x)+cos2(π 2 +x) (1)求函数 f(x)的单调递增区间 (2)若 f(α)=13 10 (π 3 <α<7π 12 )，求 sin2α的值 20. (本题满分 12 分) 已知在△ABC 中，内角 A、B、C 对应的边分别为 a、b、c，且 acosC+ccosA=2bcosB，b= 3 (1)求证：角 A、B、C 成等差数列 (2)求△ABC 面积的最大值 21. (本题满分 12 分) 已知椭圆x2 a2+y2 b2 =1(a>b>0)的左右焦点分别为 21 FF 和 ,离心率为 e=1 2 ，点 P 椭圆上的一个 动点，△PF1F2 的面积的最大值为 34 (1)求椭圆的方程 (2)若A、B、C、D是椭圆上不重合的四个点，AC与BD相交于点F1，且→AC·→BD=0,求|→AC|+|→BD| 的取值范围。 22. (本题满分 12 分) 已知函数 Raxx axf  ,2ln)( (1)当 8a 时，求函数 )(xf 的单调区间 (2)是否存在实数 a ，使得函数 )(xf 在 ],0( 2e 上有最小值 2？若存在，求出 a 的值，若 不存在，请说明理由 请考生在第 22 和 23 题中任选一个作答，如果多做，按所做的第一题计分 23. (本题满分 10 分)选修 4-4：坐标系与参数方程 在平面直角坐标系 xOy 中，直线l 的参数方程为 x=3- 2 2 t y= 5+ 2 2 t(t 为参数)，在极坐标系(与 直角坐标系 xOy 取相同的长度单位，且以原点 O 为极点，以 x 轴正半轴为极轴)中，圆 C 的极坐标方程为ρ=2 5 sinθ (1)求直线l 的普通方程和圆 C 的直角坐标方程 (2)设圆 C 与直线l 交于 A,B 两点，若点 P 的坐标为(3, 5)，求|PA|+|PB| 24. (本题满分 10 分)选修 4-5：不等式选讲 已知函数 f(x)=2|2x+1|+|2x-2|的最小值为 m (1)求 m 的值 (2)设正数 cba ,, 满足 mcba  ，求证： mcba  111