2017届高考文科数学(全国通用)二轮适考素能特训:2017年高考全真模拟试题2
2017年高考全真模拟试题(二)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试时间120分钟,满分150分.
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U=R,集合A={x|x<2},B={x|lg(x-1)>0},则A∩(∁UB)=( )
A.{x|1
2},∴∁UB={x|x≤2},∴A∩(∁UB)={x|x<2},故选C.
2.定义运算=ad-bc,则符合条件=0的复数z的共轭复数在复平面内对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
解析 由题意得,2zi-[-i(1+i)]=0,则z==--,∴=-+,其在复平面内对应的点在第二象限,故选B.
3.下列说法中,不正确的是( )
A.已知a,b,m∈R,命题:“若am20”的否定是:“∀x∈R,x2-x≤0”
C.命题“p或q”为真命题,则命题p和命题q均为真命题
D.“x>3”是“x>2”的充分不必要条件
答案 C
解析 本题考查命题真假的判断.命题“p或q”为真命题,则命题p和命题q中至少有一个为真命题,C错误,故选C.
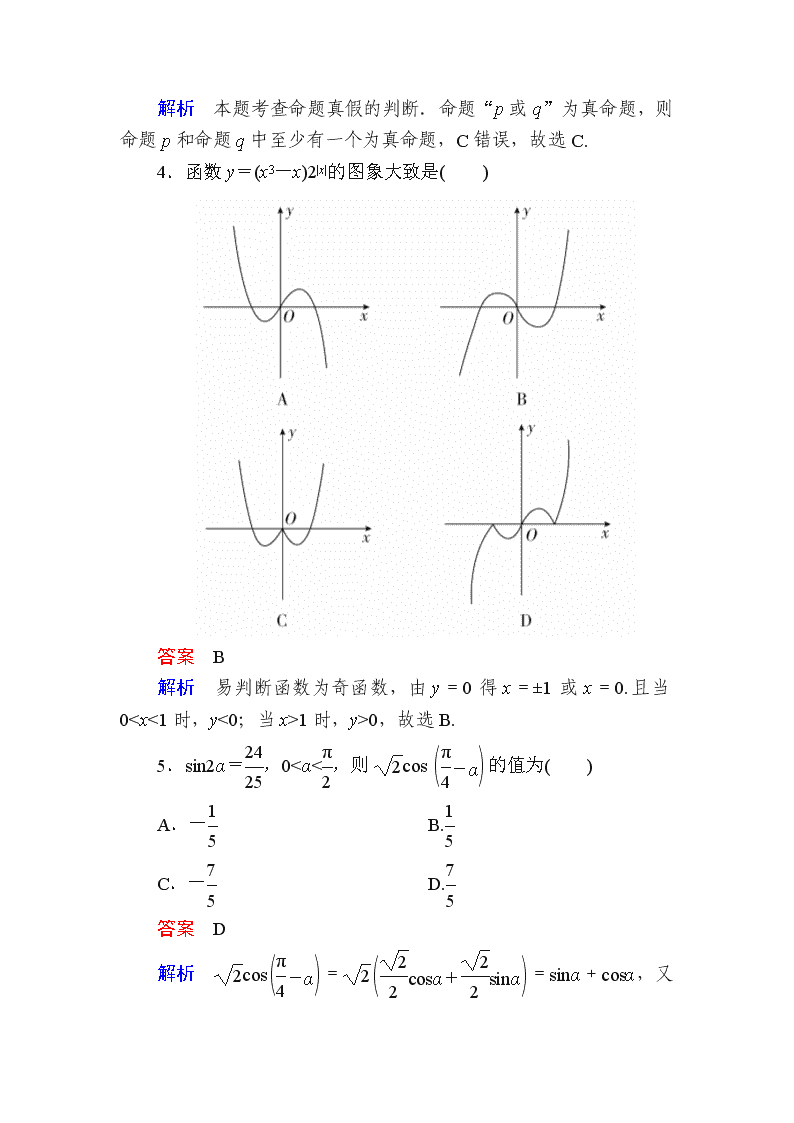
4.函数y=(x3-x)2|x|的图象大致是( )
答案 B
解析 易判断函数为奇函数,由y=0得x=±1或x=0.且当01时,y>0,故选B.
5.sin2α=,0<α<,则cos的值为( )
A.- B.
C.- D.
答案 D
解析 cos==sinα+cosα,又∵(sin
α+cosα)2=1+2sinαcosα=1+sin2α=,0<α<,∴sinα+cosα=,故选D.
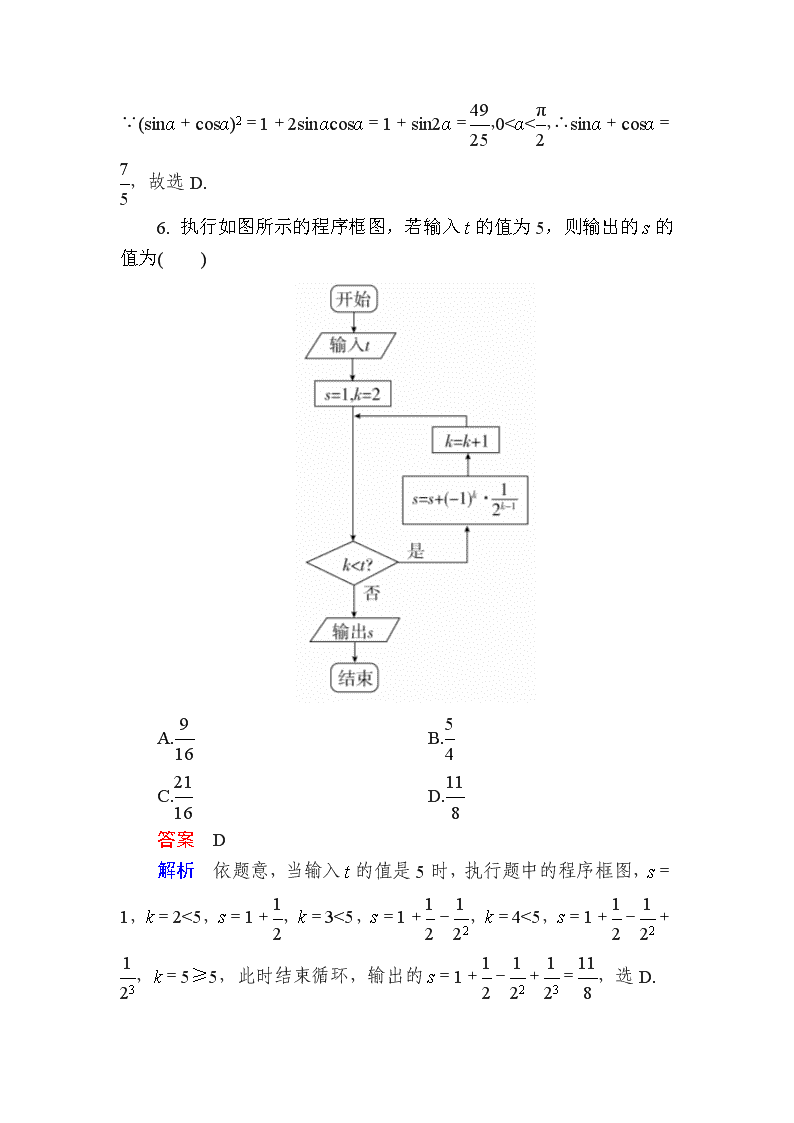
6. 执行如图所示的程序框图,若输入t的值为5,则输出的s的值为( )
A. B.
C. D.
答案 D
解析 依题意,当输入t的值是5时,执行题中的程序框图,s=1,k=2<5,s=1+,k=3<5,s=1+-,k=4<5,s=1+-+,k=5≥5,此时结束循环,输出的s=1+-+=,选D.
7.某几何体的三视图如图所示,则该几何体的体积是( )
A.2π- B.2π-
C. D.2π-2
答案 A
解析 本题考查几何体的三视图和体积.由三视图得该几何体为底面半径为1,高为2的圆柱体挖去一个底面边长为的正方形,高为1的正四棱锥后剩余的部分,则其体积为2×π×12-×()2×1=2π-,故选A.
8.将函数f(x)=sin(2x+φ)的图象向右平移个单位后的图象关于y轴对称,则函数f(x)在上的最小值为( )
A.0 B.-1
C.- D.-
答案 D
解析 f(x)=sin(2x+φ)的图象向右平移个单位后得到g(x
)=sin=sin的图象,又g(x)的图象关于y轴对称,
∴g(0)=sin=±1,
∴-+φ=+kπ(k∈Z),
∴φ=+kπ(k∈Z),又|φ|<,
∴φ=-,∴f(x)=sin,又x∈,
∴2x-∈,∴f(x)min=-.
9.设不等式组,所表示的区域为M,函数y=的图象与x轴所围成的区域为N,向M内随机投一个点,则该点落在N内的概率为( )
A. B.
C. D.
答案 B
解析 本题考查不等式组表示的平面区域、几何概型.在平面直角坐标系内画出题中的不等式组表示的平面区域为以(,0),(-,0),(0,)为顶点的三角形区域,函数y=的图象与x轴围成的区域如图中的阴影部分所示,则所求概率为=,故选B.
10.如图,在正六边形ABCDEF中,点P是△CDE内(包括边界)的一个动点,设=λ+μ(λ,μ∈R),则λ+μ的取值范围是( )
A.
B.[3,4]
C.
D.
答案 B
解析 本题考查平面向量的运算、线性规划的应用.以A为原点,分别以AB,AE所在的直线为x,y轴建立平面直角坐标系,设正六边形的边长为1,则A(0,0),B(1,0),C,D(1,),E(0,
),F,设点P(x,y),则=(x,y),=,=(1,0),则由=λ+μ得解得则λ+μ=x+y,又因为点P在△CDE内,所以当点P与点D重合时,λ+μ取得最大值1+×=4,当点P在线段CE上时,λ+μ取得最小值3,所以λ+μ的取值范围为[3,4],故选B.
11.在平面直角坐标系xOy中,点P为椭圆C:+=1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,α∈,则椭圆C的离心率的取值范围为( )
A. B.
C. D.
答案 A
解析 因为OP在y轴上,在平行四边形OPMN中,MN∥OP,因此M,N的横坐标相等,纵坐标互为相反数,即M,N关于x轴对称,|MN|=|OP|=a,可设M(x,-y0),N(x,y0).由kON=kPM得y0=.把点N的坐标代入椭圆方程得|x|=b,点N.因为α是直线ON的倾斜角,因此tanα=÷b=.又α∈,因此0时,g′(x)<0,g(x)单调递减.又f(x)是偶函数,则g(-x)=x2f(-x)-x2=x2f(x)-x2=g(x),即g(x)是偶函数.不等式x2f(x)-f(1)1,解得x<-1或x>1,选项B正确.
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.
二、填空题(本大题共4小题,每小题5分)
13.某单位有员工90人,其中女员工有36人,为做某项调查,拟采用分层抽样法抽取容量为15的样本,则男员工应选取的人数是________.
答案 9
解析 男员工应抽取的人数为×15=9.
14.已知三棱锥P-ABC的顶点P、A、B、C在球O的球面上,△ABC是边长为的等边三角形,如果球O的表面积为36π,那么P到平面ABC距离的最大值为________.
答案 3+2
解析 依题意,边长是的等边△ABC的外接圆半径r=·=1,∵球O的表面积为36π=4πR2,∴球O的半径R=3,∴球心O到平面ABC的距离d==2,∴球面上的点P到平面ABC距离的最大值为R+d=3+2.
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,如果△ABC的面积等于8,a=5,tanB=-,那么
=________.
答案
解析 △ABC中,∵tanB=-,∴sinB=,cosB=-,又S△ABC=acsinB=2c=8,∴c=4,∴b==,∴==.
16.过直线l:x+y=2上任意一点P向圆C:x2+y2=1作两条切线,切点分别为A,B,线段AB的中点为Q,则点Q到直线l的距离的取值范围为________.
答案
解析 依题意,设点P(x0,2-x0),则直线AB的方程为x0x+(2-x0)y=1(注:由圆x2+y2=r2外一点E(x0,y0)向该圆引两条切线,切点分别为F,G,则直线FG的方程是x0x+y0y=r2),直线OP的方程是(2-x0)x-x0y=0,其中点Q是直线AB与OP的交点,因此点Q(x,y)的坐标是方程组的解.
由得
即点Q,点Q到直线l的距离d==.
注意到0<=≤1,-2<-2≤-1,1≤<2,所以≤<,即点Q到直线l
的距离的取值范围是.
三、解答题(解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)已知等比数列{an}的前n项和Sn满足:S3=39,且2a2是3a1与a3的等差中项.
(1)求数列{an}的通项an;
(2)若数列{an}为递增数列,bn=,Tn=b1+b2+…+bn,问是否存在正整数n使得Tn>成立?若存在,求出n的最小值;若不存在,请说明理由.
解 (1)设数列{an}的公比为q.
由S3=39得a1(1+q+q2)=39. ①
因为2a2是3a1与a3的等差中项,则3a1+a3=4a2.
即q2-4q+3=0,解得q=1或q=3.
代入①式得:当q=1时,a1=13,{an}的通项公式为an=13;
当q=3时,a1=3,{an}的通项公式为an=3×3n-1=3n.
(2)因为数列{an}为递增数列,所以an=3n,bn===.
Tn=
=.
由Tn>得n2-n-4>0,即n>.
又n∈N*,所以存在最小正整数n=3,使得Tn>成立.
18.(本小题满分12分)2016年1月19日,习近平主席开启对沙特、埃及、伊朗为期5天的国事访问.某校高二文科一班主任为了解同学们对此事的关注情况,在该班进行了一次调查,发现在全班50名同学中,对此事关注的同学有30名.该班在本学期期末考试中政治成绩(满分100分)的茎叶图如下:
(1)求“对此事不关注者”的政治期末考试成绩的中位数与平均数;
(2)若成绩不低于60分记为“及格”,从“对此事不关注者”中随机抽取1人,该同学及格的概率为P1,从“对此事关注者”中随机抽取1人,该同学及格的概率为P2,求P2-P1的值;
(3)若成绩不低于80分记为“优秀”,请以是否优秀为分类变量.
①补充下面的2×2列联表;
政治成
绩优秀
政治成
绩不优秀
合计
对此事关注
者(单位:人)
对此事不关注
者(单位:人)
合计
②是否有90%以上的把握认为“对此事是否关注”与政治期末成绩是否优秀有关系?
参考数据:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:K2=,其中n=a+b+c+d.
解 (1)“对此事不关注者”的20名同学,成绩从低到高依次为:
42,46,50,52,53,56,61,61,63,64,66,66,72,72,76,82,82,86,90,94,
中位数为=65,
平均数为
=66.7.
(2)由条件可得P1==,P2==,
所以P2-P1=-=.
(3)①补充的2×2列联表如下:
政治成
绩优秀
政治成
绩不优秀
合计
对此事关注
者(单位:人)
12
18
30
对此事不关注
者(单位:人)
5
15
20
合计
17
33
50
②由2×2列联表可得
K2==≈1.203<2.706,
所以,没有90%以上的把握认为“对此事是否关注”与政治期末成绩是否优秀有关系.
19.[2016·福建质检](本小题满分12分)如图,三棱柱ABC-
A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,求三棱锥A1-ABD的体积.
解 解法一:(1)证明:连接AB1交A1B于点O,则O为AB1的中点,
∵D是AC的中点,
∴DO为△ACB1的中位线,
∴OD∥B1C.
又OD⊂平面A1BD,B1C⊄平面A1BD,
∴B1C∥平面A1BD.
(2)∵AC=2,BC=1,∠ACB=60°,
∴AB2=AC2+BC2-2AC·BC·cos∠ACB=3,
∴AB=,且△ABC为直角三角形.
取AB的中点M,连接A1M,
∵AB=BB1=AA1,∠A1AB=60°,
∴△ABA1为等边三角形,
∴A1M⊥AB,且A1M=.
又∵平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,
A1M⊂平面AA1B1B,
∴A1M⊥平面ABC.
∵S△ABD=S△ABC=,
∴V三棱锥A1-ABD=S△ABD·A1M=.
解法二:(1)证明:取A1C1的中点D1,连接B1D1,CD1,DD1,
∵A1D1=A1C1,
CD=AC,A1C1綊AC,
∴A1D1綊CD,
∴四边形A1DCD1为平行四边形,
∴CD1∥A1D.
又A1D⊂平面A1BD,CD1⊄平面A1BD,
∴CD1∥平面A1BD.
∵BB1綊AA1綊DD1,
∴四边形D1DBB1为平行四边形,
∴B1D1∥BD.
又BD⊂平面A1BD,B1D1⊄平面A1BD,
∴B1D1∥平面A1BD.
又CD1∩B1D1=D1,
∴平面B1CD1∥平面A1BD.
又B1C⊂平面B1CD1,∴B1C∥平面A1BD.
(2)∵AC=2,BC=1,∠ACB=60°,
∴AB2=AC2+BC2-2AC·BC·cos∠ACB=3,
∴AB=.
∴AC2=AB2+BC2,∴BC⊥AB.
又∵平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,
∴BC⊥平面AA1B1B.
∵∠A1AB=60°,AB=BB1=AA1,
∴AA1=,
∴S△A1AB=AB·AA1·sin∠A1AB=.
∵D是AC的中点,
∴V三棱锥A1-ABD=V三棱锥D-A1AB=V三棱锥C-A1AB
=×S△A1AB·BC=.
20.(本小题满分12分)已知椭圆C:+=1(a>b>0)的离心率为,过点M(1,0)的直线l交椭圆C于A,B两点,|MA|=λ|MB|,且当直线l垂直于x轴时,|AB|=.
(1)求椭圆C的方程;
(2)若λ∈,求弦长|AB|的取值范围.
解 (1)由已知e=,得=,
又当直线垂直于x轴时,|AB|=,所以椭圆过点,
代入椭圆方程得+=1,
∵a2=b2+c2,联立方程可得a2=2,b2=1,
∴椭圆C的方程为+y2=1.
(2)当过点M的直线斜率为0时,点A,B分别为椭圆长轴的端点,
λ===3+2>2或λ===3-2<,不符合题意.
∴直线的斜率不能为0.
设直线方程为x=my+1,A(x1,y1),B(x2,y2),
将直线方程代入椭圆方程得:
(m2+2)y2+2my-1=0,由根与系数的关系可得,
将①式平方除以②式可得:
++2=-,
由已知|MA|=λ|MB|可知,=-λ,
∴-λ-+2=-,
又知λ∈,∴-λ-+2∈,
∴-≤-≤0,解得m2∈.
|AB|2=(1+m2)|y1-y2|2=(1+m2)[(y1+y2)2-4y1y2]=82=82,
∵m2∈,∴∈,
∴|AB|∈.
21.[2016·福建质检](本小题满分12分)已知函数f(x)=ln x+-1,a∈R.
(1)若函数f(x)的最小值为0,求a的值;
(2)证明:ex+(ln x-1)sinx>0.
解 (1)f(x)=ln x+-1的定义域为(0,+∞),
且f′(x)=-=.
若a≤0,则f′(x)>0,于是f(x)在(0,+∞)上单调递增,
故f(x)无最小值,不符合题意.
若a>0,则当0a时,f′(x)>0.
故f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.
于是当x=a时,f(x)取得最小值ln a.
由已知得ln a=0,解得a=1.
综上,a=1.
(2)证明:①下面先证当x∈(0,π)时,ex+(ln x-1)sinx>0.
因为x∈(0,π),所以只要证>1-ln x.
由(1)可知≥1-ln x,
于是只要证>,即只要证xex-sinx>0.
令h(x)=xex-sinx,则h′(x)=(x+1)ex-cosx.
当01·e0-1=0,
所以h(x)在(0,π)上单调递增.
所以当0h(0)=0,即xex-sinx>0.
故当x∈(0,π)时,不等式ex+(ln x-1)sinx>0成立.
②当x∈[π,+∞)时,由(1)知≥1-ln x,
于是有x≥1-ln,即x≥1+ln x.
所以ex≥e1+ln x,即ex≥ex,
又因为ex≥e(1+ln x),所以ex≥e(1+ln x),
所以ex+(ln x-1)sinx≥e(ln x+1)+(ln x-1)sinx
=(e+sinx)ln x+(e-sinx)>0.
综上,不等式ex+(ln x-1)sinx>0成立.
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=2sinθ.
(1)写出直线l的普通方程和圆C的直角坐标方程;
(2)若点P坐标为(3,),圆C与直线l交于A、B两点,求|PA|+|PB|的值.
解 (1)由得直线l的普通方程为x+y-3-=0.
又由ρ=2sinθ得圆C的直角坐标方程为x2+y2-2y=0,
即x2+(y-)2=5.
(2)把直线l的参数方程代入圆C的直角坐标方程,得
2+2=5,即t2-3t+4=0.
由于Δ=(3)2-4×4=2>0,故可设t1、t2是上述方程的两实数根,
所以t1+t2=3,t1·t2=4.
又直线l过点P(3, ),A、B两点对应的参数分别为t1、t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3.
23.(本小题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-a|(a∈R).
(1)当a=4时,求不等式f(x)≥5的解集.
(2)若f(x)≥4对a∈R恒成立,求实数a的取值范围.
解 (1)当a=4时,|x-1|+|x-a|≥5等价于
或或
解得x≤0或x≥5.
所以不等式f(x)≥5的解集为{x|x≤0或x≥5}.
(2)因为f(x)=|x-1|+|x-a|≥|(x-1)-(x-a)|=|a-1|,所以f(x)min=|a-1|.
要使f(x)≥4对a∈R恒成立,则|a-1|≥4即可,
所以a≤-3或a≥5,
即实数a的取值范围是{a|a≤-3或a≥5}.