人教版高三数学总复习课时作业14
课时作业14 导数与函数单调性
一、选择题
1.下面为函数y=xsinx+cosx的递增区间的是( )
A.(,) B.(π,2π)
C.(,) D.(2π,3π)
解析:y′=(xsinx+cosx)′=sinx+xcosx-sinx=xcosx,当x∈(,)时,恒有xcosx>0.故选C.
答案:C
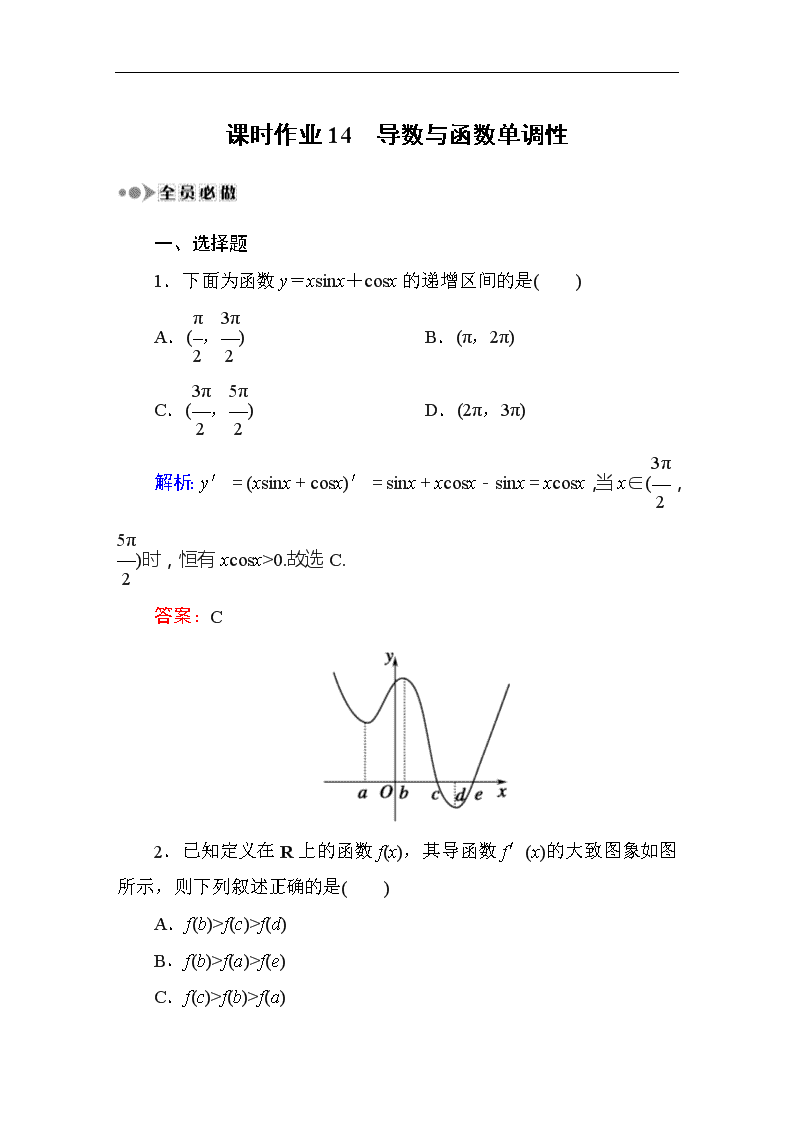
2.已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )
A.f(b)>f(c)>f(d)
B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a)
D.f(c)>f(e)>f(d)
解析:依题意得,当x∈(-∞,c)时,f′(x)>0;当x∈(c,e)时,
f′(x)<0;当x∈(e,+∞)时,f′(x)>0.因此,函数f(x)在(-∞,c)上是增函数,在(c,e)上是减函数,在(e,+∞)上是增函数,又a
f(b)>f(a).
答案:C
3.∀x1,x2∈(0,),x2>x1,y1=,y2=,则( )
A.y1=y2
B.y1>y2
C.y1y2.
答案:B
4.设函数f(x)=x2-9lnx在区间[a-1,a+1]上单调递减,则实数a的取值范围是( )
A.10),
当x-≤0时,有00且a+1≤3,解得1f(b) B.f(a)=f(b)
C.f(a)1
解析:f′(x)=,当x>e时,f′(x)<0,则f(x)在(e,+∞)上为减函数,f(a)>f(b).
答案:A
二、填空题
7.函数f(x)=1+x-sinx在(0,2π)上的单调情况是________.
解析:在(0,2π)上有f′(x)=1-cosx>0,所以f(x)在(0,2π)上单调递增.
答案:单调递增
8.若函数f(x)=x3-x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
解析:∵f(x)=x3-x2+ax+4,∴f′(x)=x2-3x+a,又函数f(x)恰在[-1,4]上单调递减,∴-1,4是f′(x)=0的两根,∴a=(-1)×4=-4.
答案:-4
9.若函数f(x)=(a>0)为R上的单调函数,则a的取值范围为________.
解析:若f(x)为R上的单调函数,则f′(x)在R上不变号,结合f′(x)=ex与条件a>0,知ax2-2ax+1≥0在R上恒成立,因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知00),则h′(x)=--<0,即h(x)在(0,+∞
)上是减函数.
由h(1)=0知,当00,从而f′(x)>0;
当x>1时,h(x)<0,从而f′(x)<0.
综上可知,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).
11.已知函数f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
解:(1)对f(x)求导,得f′(x)=3x2-2ax-3.
由f′(x)≥0,得a≤.
记t(x)=,当x≥1时,t(x)是增函数,
∴t(x)min=(1-1)=0.∴a≤0.
(2)由题意,得f′(3)=0,即27-6a-3=0,
∴a=4.∴f(x)=x3-4x2-3x,
f′(x)=3x2-8x-3.
令f′(x)=0,得x1=-,x2=3.
当x变化时,f′(x)、f(x)的变化情况如下表:
x
-
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
极大值
极小值
∴f(x)的单调递增区间为,[3,+∞),f(x
)的单调递减区间为.
1.函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=在区间(1,+∞)上一定( )
A.有最小值 B.有最大值
C.是减函数 D.是增函数
解析:由函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,可得a<1,又g(x)==x+-2a,则g′(x)=1-,易知在x∈(1,+∞)上g′(x)>0,所以g(x)在(1,+∞)上为增函数.
答案:D
2.已知f(x)为R上的可导函数,且∀x∈R,均有f(x)>f′(x),则以下判断正确的是( )
A.f(2 013)>e2 013f(0)
B.f(2 013)f′(x),∴g′(x)<0,即函数g(x)在R上递减,∴g(2 013)0,函数f(x)在(0,+∞)上单调递增,
当a<0时,令g(x)=ax2+(2a+2)x+a,
由于Δ=(2a+2)2-4a2=4(2a+1).
①当a=-时,Δ=0,
f′(x)=≤0,函数f(x)在(0,+∞)上单调递减.
②当a<-时,Δ<0,g(x)<0,
f′(x)<0,函数f(x)在(0,+∞)上单调递减.
③当-0,
设x1,x2(x10,
所以x∈(0,x1)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
x∈(x1,x2)时,g(x)>0,f′(x)>0,函数f(x)单调递增,
x∈(x2,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减.
综上可得:
当a≥0时,函数f(x)在(0,+∞)上单调递增;
当a≤-时,函数f(x)在(0,+∞)上单调递减;
当-
查看更多