- 2021-06-20 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年高考数学(理)二轮复习讲练测 专题23 立体几何角的计算问题(讲)(原卷版)
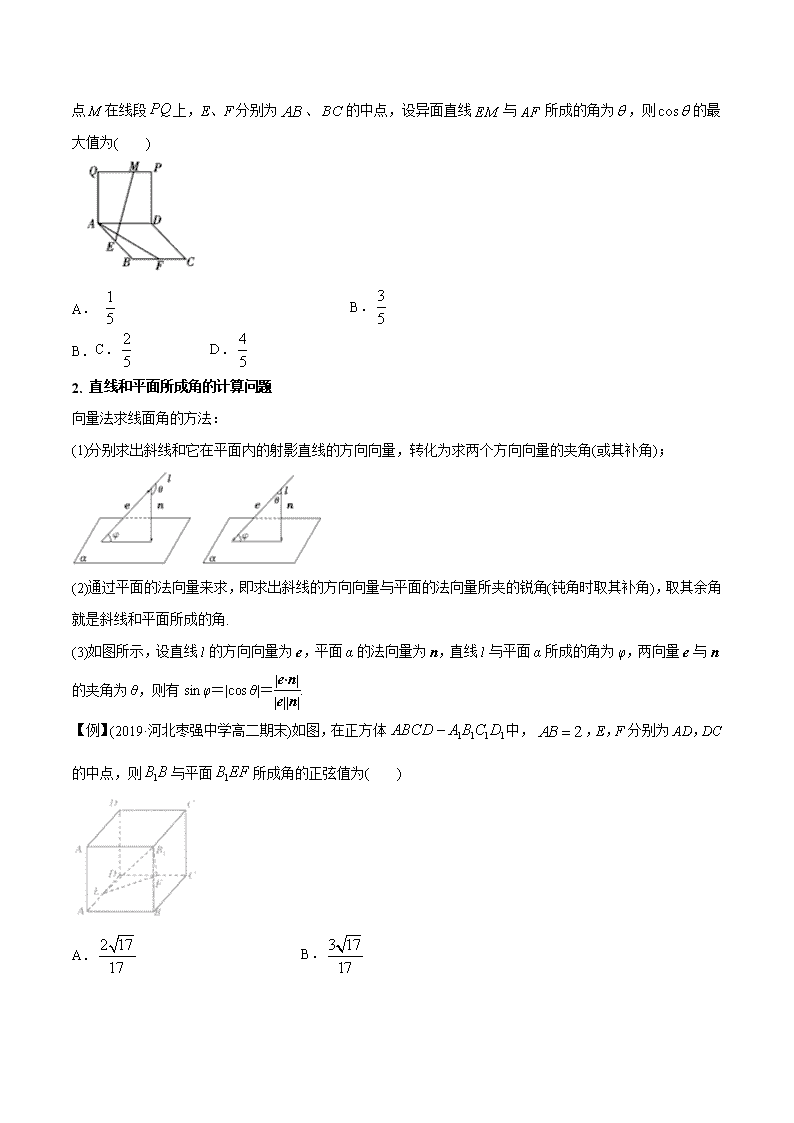
专题23 立体几何角的计算问题 在立体几何命题中,判定和证明空间的线线、线面以及面面之间的位置关系(主要是平行与垂直的位置关系),计算空间图形中的几何量(主要是角与距离)是两类基本问题.正确揭示空间图形与平面图形的联系,并有效地实施空间图形与平面图形的转换是分析和解决这两类问题的关键.空间的角与距离的计算(特别是角的计算)是高考热点,一般以大题的条件或一小问形式呈现,考查用向量方法解决立体几何问题,将空间几何元素之间的位置关系转化为数量关系,并通过计算解决立体几何问题.本文就高考命题中立体几何角的计算问题加以总结探讨,以提高高考获取高分. 1.异面直线所成的角的计算问题 ①定义:设a,b是两条异面直线,过空间任一点O作直线a′∥a,b′∥b,则a′与b′所夹的锐角或直角叫做a与b所成的角. ②范围:两异面直线所成角θ的取值范围是. ③向量求法:设直线a,b的方向向量为a,b,其夹角为φ,则有.利用直线的方向向量的夹角求异面直线的夹角时,注意区别:当异面直线的方向向量的夹角为锐角或直角时,就是此异面直线所成的角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线所成的角. ④几何法:求异面直线所成角的步骤:一平移,将两条异面直线平移成相交直线.二定角,根据异面直线所成角的定义找出所成角.三求角,在三角形中用余弦定理或正弦定理或三角函数求角.四结论. 【例】(2019·河南高一期末)长方体中,,则异面直线与所成角的余弦值为( ) A. B. C. D. 【例】(2019·山西高三(文))在四棱锥中,平面平面,为等边三角形,四边形为直角梯形,其中,,若,分别是线段与线段的中点,则直线和所成角的余弦值为( ) A. B. C. D. 【例】(2019·四川高二期末(理))如图,四边形和 均为正方形,它们所在的平面互相垂直,动点M在线段上,E、F分别为、的中点,设异面直线与所成的角为,则的最大值为( ) A. B. B. C. D. 2. 直线和平面所成角的计算问题 向量法求线面角的方法: (1)分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角); (2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角),取其余角就是斜线和平面所成的角. (3)如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sin φ=|cos θ|=. 【例】(2019·河北枣强中学高二期末)如图,在正方体中,,E,F分别为AD,DC的中点,则与平面所成角的正弦值为( ) A. B. C. D. 【例】(2019·四川高二期末(理))在中,,是的中点,平面,如果、与平面成的角分别是30°和60°,那么与平面所成的角为( ) A.30° B.45° C.60° D.75° 21.(2019·陕西西安中学高二期末(理))如图,正三角形ABE与菱形ABCD所在的平面互相垂直,,,M是AB的中点. (1)求证:; (2)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为, 若存在,求出的值;若不存在,说明理由. 3. 二面角的计算问题 (1)二面角的平面角及其求法有:定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等,依据题目选择方法求出结果. (2)如图1,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=〈,〉. (3)如图2、3,分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小(或 ). 【例】(2019·天津南开中学高二期中(理))已知四面体中,,,,则二面角的余弦值为( ) A. B. C. D. 【例】(2019·湖南长沙一中高二月考)如图,多面体中,四边形为矩形,二面角为, ,,,. (1)求证:平面; (2)在线段上求一点,使锐二面角的余弦值为. 【例】【2018年全国卷Ⅲ理】如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点. (1)证明:平面平面; (2)当三棱锥体积最大时,求面与面所成二面角的正弦值. 【反思提升】 (1)运用空间向量坐标运算求空间角的一般步骤:①建立恰当的空间直角坐标系;② 求出相关点的坐标;③写出向量坐标;④结合公式进行论证、计算;⑤转化为几何结论. (2)求空间角注意:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|;②两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角;③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值,注意函数名称的变化.查看更多