河北省张家口市2020届高三数学(理)5月普通高等学校招生全国统一模拟试题(Word版附答案)
绝密★启用前
试卷类型:A
2020 年普通高等学校招生全国统一模拟考试
理科数学
2020.5
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1.复数 3i- 2
1
i
i
的共轭复数是
A.-1+2i B.-1-2i C.2i+1 D.-2i+1
2.集合 A={x|2x-3+x2>0},集合 B={y|y=x2-1,x∈R),则( Rð A)∩B=
A.[-1,1] B.(-1,1) C.[-1,3] D.(-1,3)
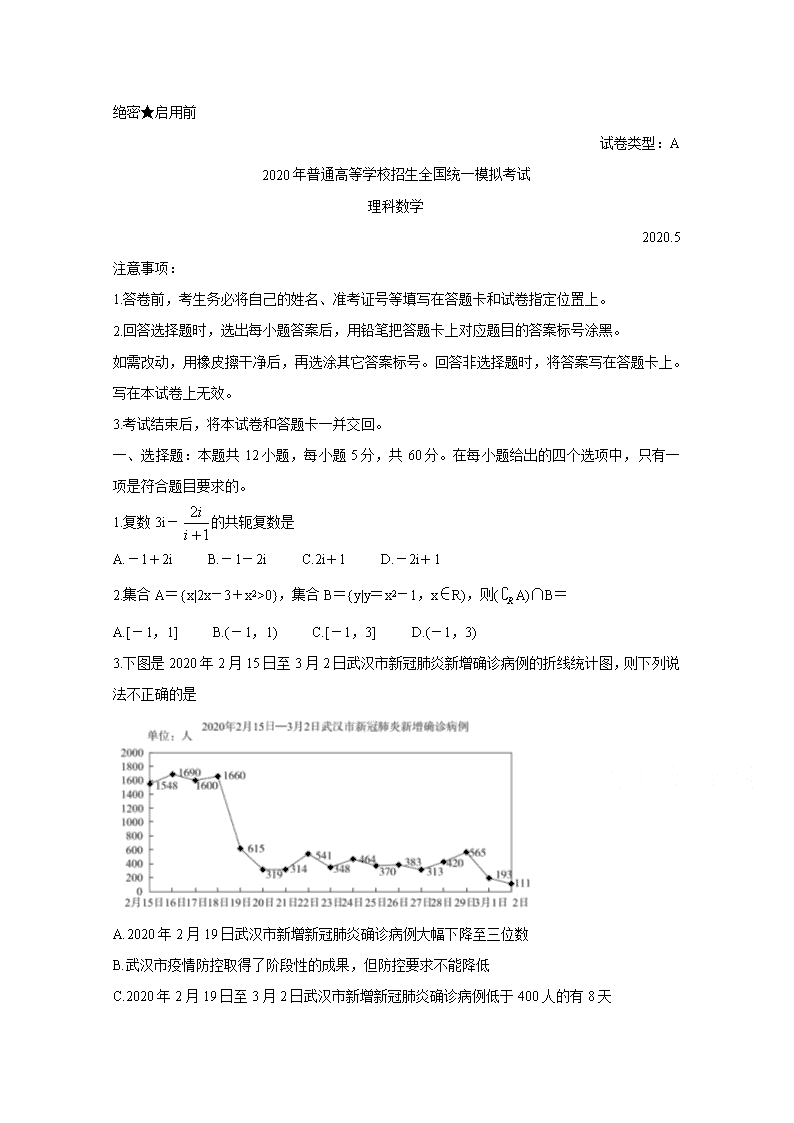
3.下图是 2020 年 2 月 15 日至 3 月 2 日武汉市新冠肺炎新增确诊病例的折线统计图,则下列说
法不正确的是
A.2020 年 2 月 19 日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市疫情防控取得了阶段性的成果,但防控要求不能降低
C.2020 年 2 月 19 日至 3 月 2 日武汉市新增新冠肺炎确诊病例低于 400 人的有 8 天
D.2020 年 2 月 15 日至 3 月 2 日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多 1549
人
4.若 0
logaa C.a1.1>a D.2
1
2 >log23
5.角谷猜想,也叫 3n+1 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如
果它是奇数,则对它乘 3 再加 1;如果它是偶数,则对它除以 2,如此循环最终都能够得到 1。
如:取 n=6,根据上述过程,得出 6,3,10,5,16,8,4,2,1,共 9 个数。若 n=13,根
据上述过程得出的整数中,随机选取两个不同的数,则两个数都是奇数的概率为
A. 1
15
B. 2
15
C. 1
18
D. 3
10
6.已知函数 f(x)是偶函数,f(x+1)为奇函数,并且当 x∈[1,2]时,f(x)=1-|x-2|,则下列选
项正确的是
A.f(x)在(-3,-2)上为减函数,且 f(x)>0 B.f(x)在(-3,-2)上为减函数,且 f(x)<0
C.f(x)在(-3,-2)上为增函数,且 f(x)>0 D.f(x)在(-3,-2)上为增函数,且 f(x)<0
7.已知双曲线
2 2
2 2 1( 0, 0)x y a ba b
的两条渐近线的倾斜角成 2 倍关系,则该双曲线的离心
率为
A. 3 B. 2 C.2 D.4
8.执行如图所示的程序框图,则输出的 S 为
A.2020 B.1010 C.1011 D.-1011
9.已知 AB
=(1,0), BC
=(-2,2)。若( AB AC
)⊥ BC
,且|µ AC
|= 10 ,则λ+μ的
值为
A.4 2 B. 4 2 C.6 2 D. 6 2
10.已知 x0 是函数 f(x)=2sinxcosx+2 3 sin2x- 3 ,x∈[-
4
,
4
]的极小值点,则 f(x0)+f(2x0)
的值为
A.0 B.-3 C.-2- 3 D.-2+ 3
11.把圆心角为 120°的扇形铁板围成一个圆锥,则该圆锥的侧面积与它的外接球的表面积之比
为
A. 3
8
B. 8
3
C. 8
27
D. 27
8
12.抛物线 C:y2=2x 的焦点为 F,点 P 在 C 上且 P 在准线上的投影为 Q,直线 QF 交 y 轴于
点 D,以 P 为圆心,PF 为半径的圆 P 与 y 轴相交于 A,B 两点,O 为坐标原点。若|OD|=2|OB|,
则圆 P 的半径为
A.3 B. 5
2
C.2 D. 3
2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.命题 p: x0∈(0,+∞),tanx0>0 的否定为 。
14.直线 y=k(x-2)与曲线 y=ex 相切,则切点的横坐标为 。
15.对于函数 f(x)=
2log 2 1
1 1
x x
a xx
,
, (a∈R)的叙述,正确的有 (写出序号即可)。
①若 a≥0,则 f(x)>0;②若 f(x)有一个零点,则-1≤a<0;③f(x)在 R 上为减函数。
16.已知 a,b,c 分别为△ABC 的三个内角 A,B,C 的对边, 2
5
bsinC+asinA=bsinB+csinC,
b=4,G 为△ABC 内一点,且GA GB GC =0,∠CAG=45°,则 AG= 。
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题,
每个试题考生都必须作答。第 22、23 题为选考题,考生根据要求作答。
(一)必考题:共 60 分。
17.(12 分)
已知数列{an}满足 a1= 1
2
,a2= 2
3
,且数列{
.
1
1a }为等差数列。
(1)求数列{an}的通项公式;
(2)令 bn= 1n
n
a
a
(n∈N*),求数列{bn}的前 n 项和 Tn。
18.(12 分)
如图,在三棱锥 P-ABC 中,PB⊥平面 ABC,平面 PAC⊥平面 PBC,PB=BC=2。
(1)证明:AC⊥平面 PBC;
(2)若二面角 B-PA-C 的余弦值为 10
10
,求线段 PA 的长。
19.(12 分)
已知椭圆 E:
2 2
2 2 1( 0)x y a ba b
的焦距为 4,且过点(-1, 14
2
)。
(1)求椭圆 E 的方程;
(2)设 A(0,b),B(0,-b),C(a,b),O(0,0),过 B 点且斜率为 k(k>0)的直线 l 交 E 于另一点
M,交 x 轴于点 Q,直线 AM 与直线 x=a 相交于点 P。证明:PQ//OC。
20.(12 分)
2019 年第十三届女排世界杯共 12 支参赛球队,比赛赛制采取单循环方式,即每支球队进行 11
场比赛,最后靠积分选出最后冠军。积分规则如下(比赛采取 5 局 3 胜制):比赛中以 3-0 或 3
-1 取胜的球队积 3 分,负队积 0 分;而在比赛中以 3-2 取胜的球。队积 2 分,负队积 1 分。
9 轮过后,积分榜上的前 2 名分别为中国队和美国队,中国队积 26 分,美国队积 22 分。第
10 轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为 p(00。
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的第一题
计分。
22.[选修 4-4:坐标系与参数方程](10 分)
在直角坐标系 xOy 中,曲线 C1:y2=ax(a<0),曲线 C2: 2cos
2 2sin
x
y
,
(θ为参数)。在以 O
为极点,x 轴的正半轴为极轴的极坐标系中,直线 l 的极坐标方程为θ= 3
4
(ρ∈R)。l 与 C1,
C2 分别交于异于极点的 A,B 两点,且 2|OB|=|OA|。
(1)写出曲线 C2 的极坐标方程;
(2)求实数 a 的值。
23.[选修 4-5:不等式选讲](10 分)
已知函数 f(x)=|x-a|+2|x|(a>0)。
(1)解不等式 f(x)≥2a;
(2)若函数 f(x)的图象与直线 y=2a 围成的图形的面积为 6,求实数 a 的值。