- 2021-06-20 发布 |
- 37.5 KB |
- 8页

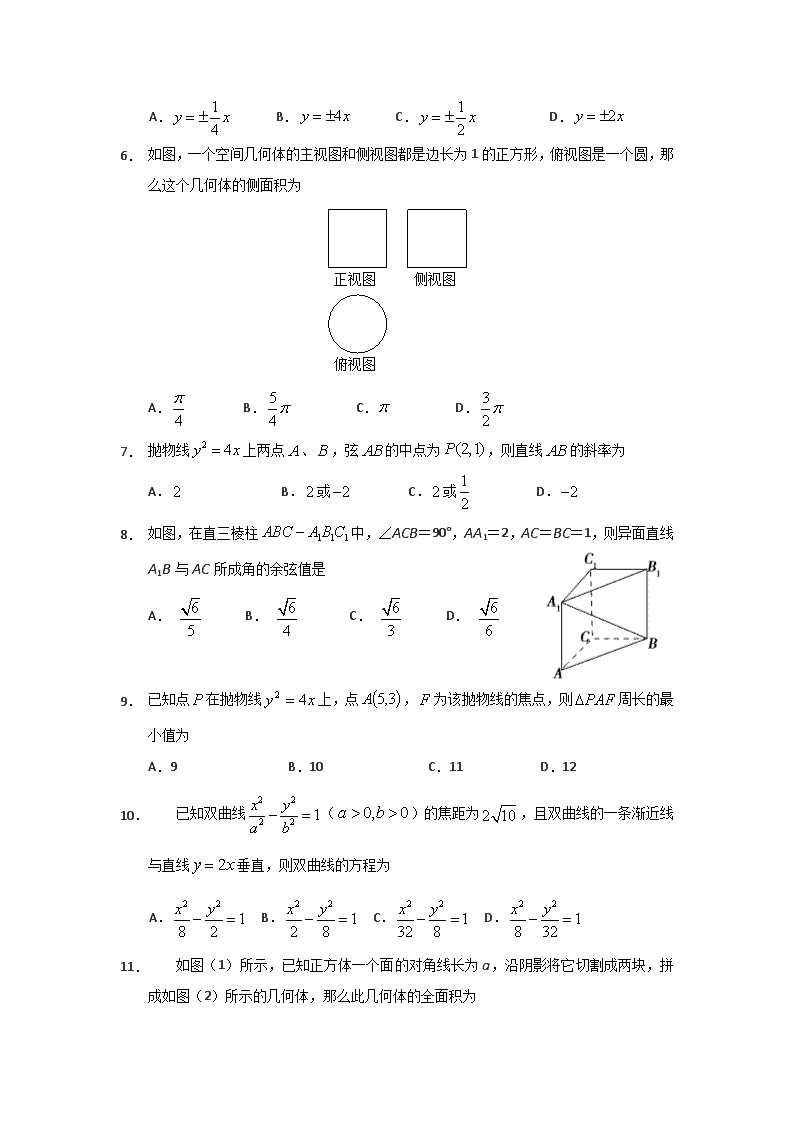

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学(理)卷·2019届黑龙江省哈三中高二上学期期中考试(2017-11)
哈尔滨市第三中学2017-2018学年高二上学期期中考试 数学(理)试卷 考试说明:(1)本试卷分第I卷(选择题)和第II卷(非选择题)两部分, 满分150分. 考试时间为120分钟; (2)第I卷,第II卷试题答案均答在答题卡上,交卷时只交答题卡. 第I卷 (选择题, 共60分) 一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 两条异面直线所成角的范围是 A. B. C. D. 2. 若满足约束条件,则的最大值为 A. B. C. D. 3. 如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 A. BD∥平面CB1D1 B. AC1⊥B1D1 C. AC1⊥平面CB1D1 D. 异面直线AD与CB1成角为60° 4. 一个三角形水平放置的直观图,是一个以为斜边的等腰直角三角形,且(如图),则原三角形的面积是 A. B.1 C. D. 5. 双曲线的两条渐近线为 A. B. C. D. 1. 如图,一个空间几何体的主视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为 正视图 侧视图 俯视图 A. B. C. D. 2. 抛物线上两点、,弦的中点为,则直线的斜率为 A. B.或 C.或 D. 3. 如图,在直三棱柱中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 A. B. C. D. 4. 已知点在抛物线上,点,为该抛物线的焦点,则周长的最小值为 A.9 B.10 C.11 D.12 5. 已知双曲线()的焦距为,且双曲线的一条渐近线与直线垂直,则双曲线的方程为 A. B. C. D. 6. 如图(1)所示,已知正方体一个面的对角线长为a,沿阴影将它切割成两块,拼成如图(2)所示的几何体,那么此几何体的全面积为 A. B. C. D. 1. 已知双曲线()的右支上一点,过点分别做双曲线的两条渐近线的平行线、,分别交渐近线于、,则平行四边形的面积 A.为定值 B.有最大值,无最小值 C.有最小值,无最大值 D.无法确定 第Ⅱ卷 (非选择题, 共90分) 二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上) 2. 已知抛物线方程是,则它准线方程为 . 3. 设为互不重合的平面,是互不重合的直线,给出下列四个命题: ① ② ③ ④若; 其中正确命题的序号为 . 4. 将一个半圆形纸片没有重叠的卷成一个圆锥(如图),则圆锥的母线与底面所成的角为 . 1. 一个三棱锥的三视图如下图所示,则该几何体的体积为 . 正视图 侧视图 俯视图 2 2 1 1 2 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 2. (本题10分) 斜率为1的直线过抛物线的焦点,与抛物线交于两点A、B,M为抛物线上的点. (I)求; (II)若,求点的坐标. 1. (本题12分) 如图,正方体中,、分别为、中点. (I)当点在棱上运动时,是否都有平面,证明你的结论; (II)若是的中点,求异面直线与所成的角的余弦值. 2. (本题12分) 如图,四面体中,,,. (I)求二面角的大小; (II)求四面体的体积. 1. (本题12分) 已知双曲线与直线有两个不同的交点. (I)求实数的取值范围; (II)若,求实数的取值范围. 2. (本题12分) 矩形纸板中,将沿折起到,使二面角为, (I)求异面直线与所成角的余弦; (II)求与平面成角的正切. 1. (本题12分) 已知抛物线L:的焦点为,直线与轴的交点为,与L的交点为,若. (I)求L的方程; x y O A B M N P Q F (II)过作抛物线L的切线与轴相交于点,点关于原点的对称点为点,过点 的直线交抛物线L于两点,交椭圆于两点,使得成立,求该椭圆长轴长的范围. 数学(理)试卷答案 一、选择题 CDDDD CADCA BA 二、填空题 13. 14. ④ 15. 16. 三、解答题 17. (Ⅰ); (Ⅱ). 18. (Ⅰ)是; (Ⅱ). 19. (Ⅰ); (Ⅱ). 20. (Ⅰ); (Ⅱ). 21. (Ⅰ); (Ⅱ). 22. (Ⅰ); (Ⅱ).查看更多