江苏省启东中学2017高考数学押题卷5

江苏省启东中学2017高考数学押题卷5

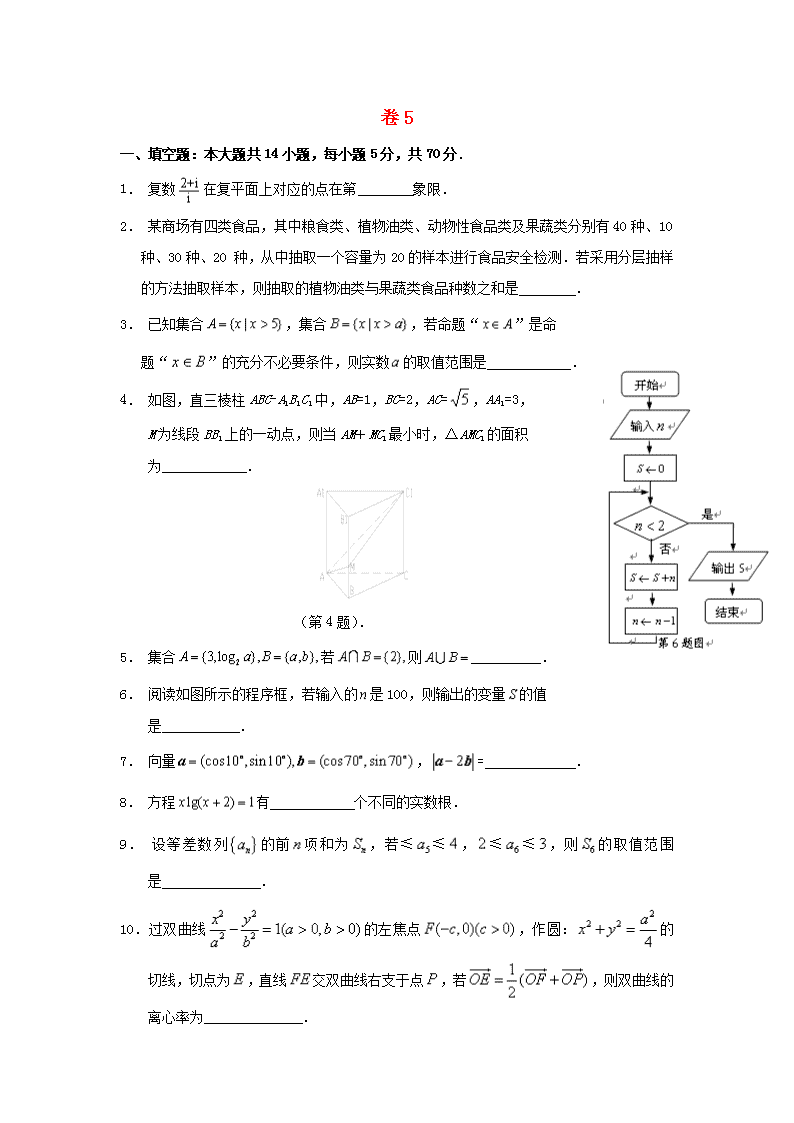
卷5‎ 一、填空题：本大题共14小题，每小题5分，共70分．‎ ‎1． 复数在复平面上对应的点在第 象限．‎ ‎2． 某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种，从中抽取一个容量为20的样本进行食品安全检测．若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是 ．‎ ‎3． 已知集合，集合，若命题“”是命 题“”的充分不必要条件，则实数的取值范围是 ．‎ ‎4． 如图，直三棱柱ABC-A1B‎1C1中，AB=1，BC=2，AC=，AA1=3，‎ M为线段BB1上的一动点，则当AM＋MC1最小时，△AMC1的面积 为 ．‎ ‎ （第4题）． ‎ ‎5． 集合若则 ．‎ ‎6． 阅读如图所示的程序框，若输入的是100，则输出的变量的值 是 ．‎ ‎7． 向量，= ．‎ ‎8． 方程有 个不同的实数根． ‎ ‎9． 设等差数列的前项和为，若≤≤，≤≤，则的取值范围是 ．‎ ‎10．过双曲线的左焦点，作圆：的切线，切点为，直线交双曲线右支于点，若，则双曲线的离心率为 ．‎ ‎11．若函数在定义域内是增函数，则实数的取值范围是 ．‎ ‎12．如果圆上总存在两个点到原点的距离为1，则实数的取值范围是 ．‎ ‎13．已知实数满足，则的最大值为 ．‎ ‎14．当为正整数时，函数表示的最大奇因数,如,设,则 ．‎ 答案 ‎1. 四 2. 6 3. 4. 5. {2,3,4} 6. 5049 7. 8. 2 9. ‎ ‎10. 11. 12. 13. 4 14. ‎ 二、解答题：本大题共六小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15．（本题满分14分）‎ 在锐角中，角，，所对的边分别为，，．已知.‎ ‎（1）求；（2）当，且时，求.‎ 解：（1）由已知可得.所以. ……………… 2分 因为在中，，所以. ………………………………4分 ‎（2）因为，所以. ………………………………6分 因为是锐角三角形，所以，. ………………8分 所以. 11分 由正弦定理可得：，所以. …………………………………………14分 说明:用余弦定理也同样给分.‎ ‎16．（本题满分14分）‎ 如图, 是边长为的正方形，平面，，.‎ ‎(1)求证：平面；‎ ‎（2）设点是线段上一个动点，试确定点的位置，‎ 使得平面，并证明你的结论.‎ 解：(1)证明：因为平面，‎ 所以. ……………………2分 因为是正方形，‎ 所以，因为………………4分 从而平面. ……………………6分 ‎（2）当M是BD的一个三等分点，即3BM＝BD时，AM∥平面BEF． …………7分 取BE上的三等分点N，使3BN＝BE，连结MN，NF，则DE∥MN，且DE＝3MN，‎ 因为AF∥DE，且DE＝3AF，所以AF∥MN，且AF＝MN，‎ 故四边形AMNF是平行四边形． ……………………………………10分 所以AM∥FN，‎ 因为AM平面BEF，FN平面BEF， …………………………………………12分 所以AM∥平面BEF． …………………………………………14分 ‎17．（本题满分14分）‎ 已知椭圆的中心为坐标原点，短轴长为2，一条准线方程为l：．‎ ‎⑴ 求椭圆的标准方程；‎ ‎⑵ 设O为坐标原点，F是椭圆的右焦点，点M是直线l上的动点，过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值．‎ 解：⑴∵椭圆C的短轴长为2，椭圆C的一条准线为l：，‎ ‎∴不妨设椭圆C的方程为．（2分）∴，（ 4分）即．（5分）‎ ‎∴椭圆C的方程为．（6分）‎ ‎ ⑵ F（1，0），右准线为l：， 设，‎ ‎ 则直线FN的斜率为，直线ON的斜率为，（8分）‎ ‎ ∵FN⊥OM，∴直线OM的斜率为，（9分）‎ ‎ ∴直线OM的方程为：，点M的坐标为．（11分）‎ ‎ ∴直线MN的斜率为．（12分）‎ ‎ ∵MN⊥ON，∴， ∴， ‎ ‎∴，即．（13分）∴为定值．（14分）‎ 说明:若学生用平面几何知识（圆幂定理或相似形均可）也得分，设垂足为P，准线l与x轴交于Q，则有，又，所以为定值．‎ ‎18．（本题满分16分）‎ 如图，直角三角形ABC中，∠B＝，AB＝1，BC＝．点M,N分别在边AB和AC ‎ 上(M点和B点不重合)，将△AMN沿MN翻折，△AMN变为△MN，使顶点落在边BC 上(点和B点不重合).设∠AMN＝．‎ ‎(1) 用表示线段的长度，并写出的取值范围；(2) 求线段长度的最小值． ‎ 解：（1）设，则．（2分）‎ 在Rt△MB中，， （4分）‎ ‎∴． （5分）‎ ‎ ∵点M在线段AB上，M点和B点不重合，点和B点不重合，∴．（7分）‎ ‎（2）在△AMN中，∠ANM＝,（8分）‎ ‎,（9分）‎ ‎＝．（10分）‎ 令＝‎ ‎＝．（13分）‎ ‎∵， ∴． （14分）‎ ‎ 当且仅当，时，有最大值，（15分）‎ ‎∴时，有最小值．（16分）‎ ‎19．（本题满分16分）‎ 已知,函数.‎ ‎(1) 如果实数满足,函数是否具有奇偶性？如果有，求出相应的 值；如果没有，说明为什么?‎ ‎(2) 如果判断函数的单调性；‎ ‎(3) 如果，，且，求函数的对称轴或对称中心.‎ 解：（1）如果为偶函数，则恒成立，（1分）‎ 即： （2分）‎ 由不恒成立，得（3分）‎ 如果为奇函数，则恒成立，（4分）‎ 即：（5分）‎ 由恒成立，得（6分）‎ ‎（2）， ∴ 当时,显然在R上为增函数；（8分）‎ 当时，，‎ 由得得得.（9分）‎ ‎∴当时, ,为减函数; （10分）‎ 当时, ,为增函数. （11分）‎ ‎(3) 当时，‎ 如果，（13分）‎ 则∴函数有对称中心（14分）‎ 如果（15分）‎ 则 ∴函数有对称轴.（16分）‎ ‎20．（本题满分16分）‎ ‎ 已知各项均不为零的数列{an}的前n项和为Sn，且满足a1＝c，2Sn＝anan＋1＋r．‎ ‎ （1）若r＝－6，数列{an}能否成为等差数列？若能，求满足的条件；若不能，请说明理由．‎ ‎ （2）设，，‎ ‎ 若r＞c＞4，求证：对于一切n∈N*，不等式恒成立．‎ 解：（1）n＝1时，‎2a1＝a‎1a2＋r，∵a1＝c≠0，∴‎2c＝ca2＋r，． （1分）‎ n≥2时，2Sn＝anan＋1＋r，① 2Sn－1＝an－1an＋r，②‎ ‎①－②，得2an＝an(an＋1－an－1)．∵an≠0，∴an＋1－an－1＝2． （ 3分）‎ 则a1，a3，a5，…，a2n－1，… 成公差为2的等差数列，a2n－1＝a1＋2(n－1)．‎ a2，a4，a6，…，a2n，… 成公差为2的等差数列， a2n＝a2＋2(n－1)．‎ 要使{an}为等差数列，当且仅当a2－a1＝1．即．r＝c－c2． （ 4分）‎ ‎∵r＝－6，∴c2－c－6＝0，c＝－2或3．‎ ‎∵当c＝－2，，不合题意，舍去.‎ ‎∴当且仅当时，数列为等差数列 （5分）‎ ‎（2）＝[a1＋2(n－1)]－[a2＋2(n－1)]＝a1－a2＝－2．‎ ‎＝[a2＋2(n－1)]－（a1＋2n）＝a2－a1－2＝－()． （8分）‎ ‎∴ （9分）‎ ‎． （10分）‎ ‎＝．（11分）‎ ‎∵r＞c＞4，∴＞4，∴＞2．∴0＜＜1． （13分）‎ 且＞－1． （14分）‎ 又∵r＞c＞4，∴，则0＜．．‎ ‎∴＜1．．∴＜1．（15分）‎ ‎∴对于一切n∈N*，不等式恒成立．（16分）‎ 附加题部分 ‎21. （选做题）本大题包括A，B，C，D共4小题，请从这4题中选做2小题. 每小题10分，共20分．请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤．‎ A．选修4－1：几何证明选讲 如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，求证：∠PDE=∠POC．‎ 证明：因AE=AC，AB为直径，‎ ‎ 故∠OAC=∠OAE． ……………………………………………………………3分 所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC．‎ 又∠EAC=∠PDE，‎ 所以，∠PDE=∠POC．…………………………………………………………10分 B．选修4—2　矩阵与变换 已知矩阵，其中，若点在矩阵的变换下得到点，‎ ‎（1）求实数a的值； ‎ ‎（2）求矩阵的特征值及其对应的特征向量.‎ 解：（1）由=，（2分） ∴. （3分）‎ ‎（2）由（1）知，则矩阵的特征多项式为 ‎ （5分）‎ 令，得矩阵的特征值为与4. （6分）‎ 当时， ‎ ‎∴矩阵的属于特征值的一个特征向量为; （8分）‎ ‎ 当时， ‎ ‎∴矩阵的属于特征值的一个特征向量为. （10分）‎ C．选修4—4　参数方程与极坐标 在平面直角坐标系xOy中，动圆（R）的 圆心为 ，求的取值范围.‎ ‎【解】由题设得（为参数，R）. …………………………5分 于是，‎ 所以 . ………………………10分 D．选修4－5：不等式选讲 已知x，y，z均为正数．求证：．‎ 证明：因为x，y，z都是为正数，所以． …………………3分 ‎ 同理可得． ‎ 将上述三个不等式两边分别相加，并除以2，得．………10分 ‎22. 必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．‎ 已知抛物线的焦点为，直线过点.‎ ‎（1）若点到直线的距离为，求直线的斜率；（4分）‎ ‎（2）设为抛物线上两点，且不与轴垂直，若线段的垂直平分线恰过点，求证：线段中点的横坐标为定值.（6分）‎ 解：（1）由已知，不合题意.设直线的方程为，‎ 由已知，抛物线的焦点坐标为， …………………1分 因为点到直线的距离为，所以， …………………2‎ 分 解得，所以直线的斜率为 . …………………4分 ‎（2）设线段中点的坐标为，，‎ 因为不垂直于轴，则直线的斜率为，直线的斜率为， ‎ 直线的方程为， …………………5分 联立方程 ‎ 消去得， …………………7分 所以， …………………8分 因为为中点，所以，即， …………………9分 所以.即线段中点的横坐标为定值. …………………10分 ‎23．必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．‎ 已知，‎ ‎（1）若，求的值；（3分）‎ ‎（2）若，求中含项的系数；（3分）‎ ‎（3）证明：．（4分）‎ 解：（1）因为,所以,又,‎ 所以 （1）‎ ‎ （2）‎ ‎（1）-（2）得：‎ 所以： …………………3分 ‎（2）因为，所以 中含项的系数为 …………………6分 ‎（Ⅲ）设 (1)‎ 则函数中含项的系数为 …………………7分 ‎ (2)‎ ‎(1)-(2)得 中含项的系数，即是等式左边含项的系数，等式右边含项的系数为 ‎ ‎ ‎ ‎ 所以 …………………10分