2018届二轮复习　函数图象与性质、函数与方程课件（全国通用）

2018届二轮复习　函数图象与性质、函数与方程课件（全国通用）

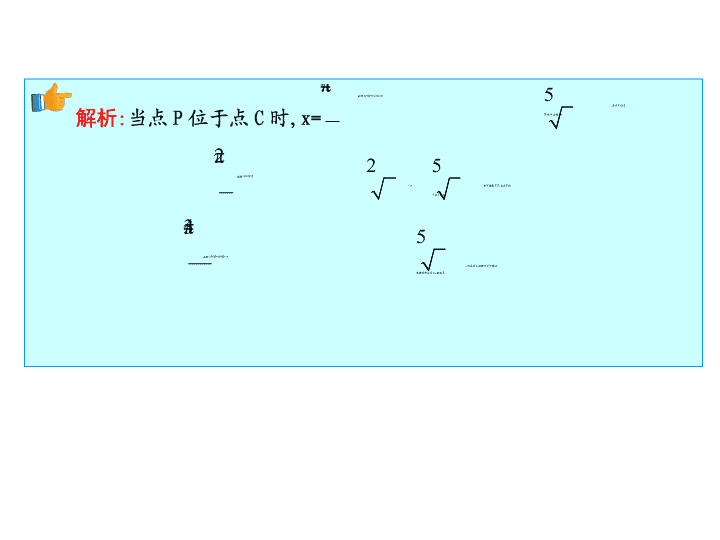
专题二　函数与导数 第 1 讲　函数图象与性质、函数与方程 高考导航 演真题 · 明备考 高考体验 1. ( 2015 · 全国 Ⅱ 卷 , 文 11 ) 如图 , 长方形 ABCD 的边 AB=2,BC=1,O 是 AB 的中点 . 点 P 沿着边 BC,CD 与 DA 运动 , 记∠ BOP=x. 将动点 P 到 A,B 两点距离之和表示为 x 的函数 f(x), 则 y=f(x) 的图象大致为 ( 　 　 ) B (A) 　 　　 　 (B) 　 (C) 　　 　　 (D) A 3.( 2016 · 全国 Ⅰ 卷 , 文 9 ) 函数 y=2x 2 -e |x| 在 [-2,2] 的图象大致为 ( 　 　 ) 解析 : 因为 f(x)=2x 2 -e |x| ,x∈[-2,2] 是偶函数 , 又 f(2)=8-e 2 ∈(0,1), 故排除 A,B. 设 g(x)=2x 2 -e x , 则 g′(x)=4x-e x . 又 g′(0)<0,g′(2)>0, 所以 g(x) 在 (0,2) 内至少存在一个极值点 , 所以 g(x)=2x 2 -e |x| 在 (0,2) 内至少存在一个极值点 , 排除 C. 故选 D. D 4.( 2016 · 全国 Ⅱ 卷 , 文 10 ) 下列函数中 , 其定义域和值域分别与函数 y=10 lg x 的定义域和值域相同的是 ( 　 　 ) (A)y=x (B)y=lg x (C)y=2 x (D)y= 解析 : 由 y=10 lg x 定义域值域均为 (0,+∞), 与 D 符合 . 故选 D. D 5.( 2015 · 全国 Ⅰ 卷 , 文 12 ) 设函数 y=f(x) 的图象与 y=2 x+a 的图象关于直线 y=-x 对称 , 且 f(-2)+f(-4)=1, 则 a 等于 ( 　 　 ) (A)-1 (B)1 (C)2 (D)4 C 解析 : 设 (x,y) 是函数 y=f(x) 图象上任意一点 , 它关于直线 y=-x 的对称点为 (-y,-x), 由 y=f(x) 的图象与 y=2 x+a 的图象关于直线 y=-x 对称 , 可知 (-y,-x) 在 y=2 x+a 的图象上 , 即 -x=2 -y+a , 解得 y=-log 2 (-x)+a, 所以 f(-2)+ f(-4)=-log 2 2+a-log 2 4+a=1, 解得 a=2, 故选 C. 6.( 2015 · 全国 Ⅱ 卷 , 文 13 ) 已知函数 f(x)=ax 3 -2x 的图象过点 (-1,4), 则 a= 　　 .   解析 : 由题意可知 (-1,4) 在函数图象上 , 即 4=-a+2, 所以 a=-2. 答案 : -2 高考感悟 1. 考查角度 (1) 函数的性质及应用 ( 定义域、值域、单调性、奇偶性、周期性、对称性 ). (2) 图象的识别、图象的应用 . (3) 函数零点的判断 , 由零点求参数 . 2. 题型及难易度 题型 : 选择题、填空题 . 难度 : 中档或偏上 . 热点突破 剖典例 · 促迁移 函数性质的应用 热点一 (2)( 2015 · 湖南卷 , 文 8 ) 设函数 f(x)=ln(1+x)-ln(1-x), 则 f(x) 是 ( 　　 ) (A) 奇函数 , 且在 (0,1) 上是增函数 (B) 奇函数 , 且在 (0,1) 上是减函数 (C) 偶函数 , 且在 (0,1) 上是增函数 (D) 偶函数 , 且在 (0,1) 上是减函数 【 方法技巧 】 函数性质的综合应用主要是指利用函数的单调性、奇偶性、周期性等性质的相互转化来解决相对综合的问题 . 主要的解题思路 : 奇偶性主要转化方向是 f(-x) 与 f(x) 的关系 ; 单调性主要转化方向是最值、方程与不等式的解 ; 周期性主要转化方向是利用 f(x)=f(x+a) 把区间外的函数转化到区间内 , 并结合单调性和奇偶性解决相关问题 . (2) 设 f(x) 是定义在 R 上的奇函数 , 当 x≤0 时 ,f(x)=2x 2 -x, 则 f(1) 等于 ( 　　 ) (A)-3 (B)-1 (C)1 (D)3 解析 : (2) 由 f(x) 是定义在 R 上的奇函数 , 故 f(1)=-f(-1)=-(2+1)=-3. 故选 A. 函数的图象及其应用 热点二 (2)( 2016 · 山东淄博二模 ) 当 a>0 时 , 函数 f(x)=(x 2 -ax)e x 的图象大致是 ( 　　 ) 【 方法技巧 】 作图、识图、用图的技巧 (1) 作图 : 常用描点法和图象变换法 . 图象变换法常用的有平移变换、伸缩变换和对称变换 . (2) 识图 : 从图象与坐标轴的交点及左、右、上、下分布范围、变化趋势、对称性等方面找准解析式与图象的对应关系 . (3) 用图 : 由函数图象确定函数性质及由方程根的存在情况求有关参数的取值范围等 . 解析 : (1) 依题意阴影部分增长由慢变快再变慢 , 对应函数 S=f(t) 的平均变化率由小变大再变小 , 切线斜率由小变大再变小 , 可得图象如 C 所示 . 故选 C. 答案 : (1)C 答案 : (2)(1,+∞) 函数与方程 热点三 考向 1 　确定零点个数或其存在区间 【 例 3】 (1)( 2016 · 湖北荆州一模 ) 函数 f(x)=ln x- 的零点所在的区间是 ( 　　 ) (A)(1,2) (B)(2,3) (C)(3,4) (D)(e,+∞) 解析 : (1) 因为 f(x)=ln x- , 则函数 f(x) 在 (0,+∞) 上单调递增 , 因为 f(2)=ln 2-1<0,f(3)=ln 3- >0, 所以 f(2)f(3)<0, 在区间 (2,3) 内函数 f(x) 存在零点 , 故选 B. (2)( 2016 · 河南郑州一模 ) 已知函数 f(x)= ( ) x -cos x, 则 f(x) 在 [0,2π] 上的零点个数为 ( 　　 ) (A)1 (B)2 (C)3 (D)4 考向 2 　根据零点的个数或其范围求参数范围 答案 : (1)D 解析 : (2) 由 y=log a (x+1)+1 在 [0,+∞) 上递减 , 得 0 时 ,f ( x+ ) =f ( x- ) , 则 f(6) 等于 ( 　　 ) (A)-2 (B)-1 (C)0 (D)2 【 例 2】 ( 2016 · 山东菏泽一模 ) 若函数 f(x)=1+ +sin x 在区间 [-k,k] (k>0) 上的值域为 [m,n], 则 m+n 等于 ( 　　 ) (A)0 (B)1 (C)2 (D)4 【 例 3】 ( 2016 · 山东济南三模 ) 函数 f(x)= 的图象大致是 ( 　　 ) 点击进入 限时训练