- 2021-06-20 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学(文)卷·2018届湖南师大附中高二下学期期中考试(2017-04)
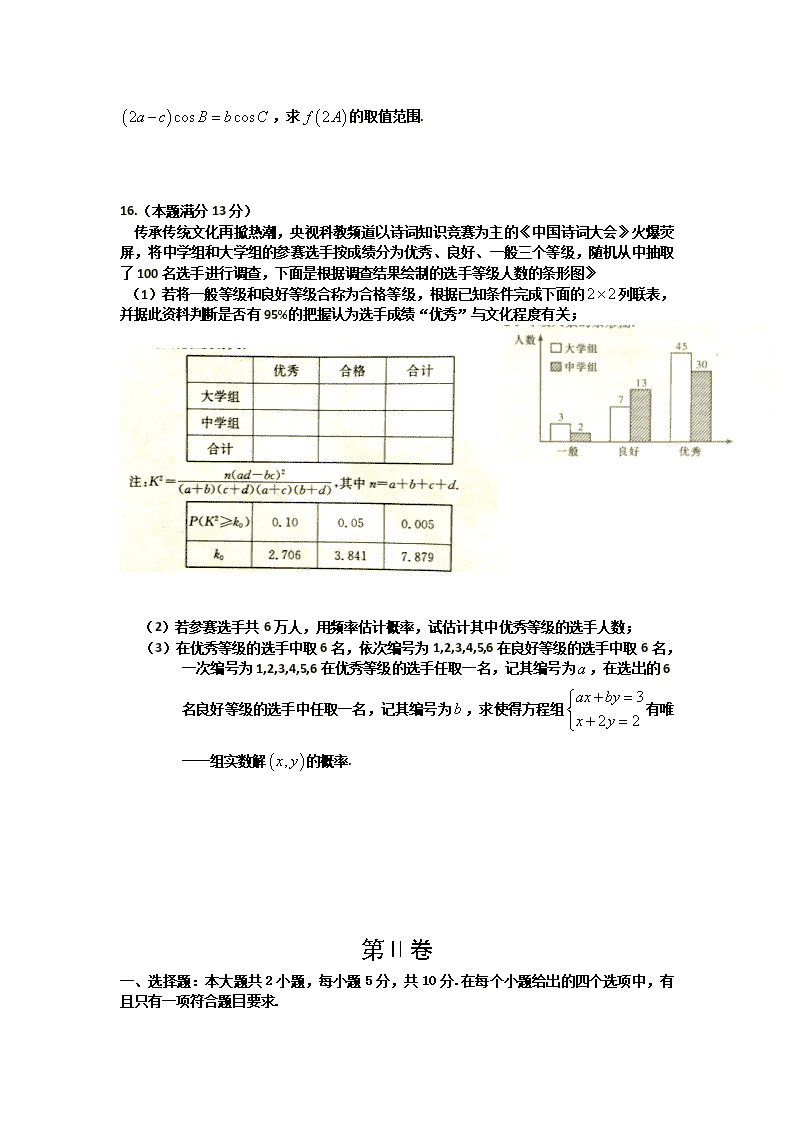
湖南师大附中2016—2017学年度高二第二学期期中考试 数学(文科) 第Ⅰ卷 一、选择题:本大题共10小题,每小题5分,共50分.在每个小题给出的四个选项中,有且只有一项符合题目要求. 1. 已知集合,则集合中的元素个数为 A. 2 B.3 C. 4 D.5 2.已知点在第三象限,则角在 A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 设,则下列关系中正确的是 A. B. C. D. 4.设,则是的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 5.如图所示的程序框图中,输出的S的值是 A.80 B.100 C.120 D.140 6. 函数的大致图象是 7.下列函数是最小正周期为的是 A. B. C. D. 8.一个空间几何体的三视图及尺寸如图所示,则该几何体的体积是 A. B. C. D. 9.已知直线与坐标轴围成的区域为M,不等式组 所形成的区域为N,现在区域M中随机放置一点,则该点落在区域N的概率为 A. B. C. D. 10. 已知定义在R上的奇函数和偶函数满足,若,则 A. 2 B. C. D. 二、填空题:本大题共3小题,每小题5分,共15分. 11.抛物线的准线与圆相切,则 . 12.已知向量,若,则 . 13.已知的面积为,则 . 三、解答题:本大题共3小题,共35分.解答应写出必要的文字说明或推理、验算过程. 14.(本题满分10分)已知数列满足,且当时,有. (1)求证:数列为等差数列,并求出数列的通项公式; (2)令,设数列的前项和为,证明:. 15.(本题满分12分)向量,记 (1)若,求的值; (2)在锐角中,角的对边分别是,且满足 ,求的取值范围. 16.(本题满分13分) 传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图》 (1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的列联表,并据此资料判断是否有95%的把握认为选手成绩“优秀”与文化程度有关; (2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数; (3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6在良好等级的选手中取6名,一次编号为1,2,3,4,5,6在优秀等级的选手任取一名,记其编号为,在选出的6名良好等级的选手中任取一名,记其编号为,求使得方程组有唯一一组实数解的概率. 第Ⅱ卷 一、选择题:本大题共2小题,每小题5分,共10分.在每个小题给出的四个选项中,有且只有一项符合题目要求. 17. 如图,在中,,则 A. B. C. D. 18.已知函数,无论取何值,函数在R上总是不单调,则实数的取值范围是 A. B. C. D. 19. 已知函数,其中为自然对数的底数,曲线上存在不同的两点,使得曲线在这两点处的切线都与轴垂直,则实数的取值范围是 A. B. C. D. 三、解答题:本大题共3小题,共35分.解答应写出必要的文字说明或推理、验算过程. 20.(本题满分10分)如图,在四棱锥中,平面,底面为菱形,为与的交点,为棱上一点.. (1)证明:平面平面; (2)若平面,求三棱锥的体积. 21.(本题满分12分) 如图,已知抛物线,过点作斜率分别为 的两条直线,与抛物线相交于点和,且分别是的中点. (1)若,求线段的长; (2)若,求面积的最小值. 22.(本题满分13分) 已知函数在处的切线与直线垂直. (1)求函数(为的导函数)的单调区间; (2)记函数,设是函数的两个极值点,若,证明:.查看更多